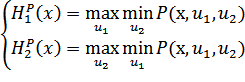8. Теорія ігор

При вирішенні низки практичних задач дослідження операцій (в області екології, забезпечення безпеки життєдіяльності і т. д.) доводиться аналізувати ситуації, в яких стикаються дві (або більше) ворогуючі сторони, що переслідують різні цілі, причому результат будь-якого заходу кожної з сторін залежить від того , який образ дій вибере супротивник. Такі ситуації ми можна віднести до конфліктних ситуацій.

Теорія ігор є математичною теорією конфліктних ситуацій, за допомогою якої можна виробити рекомендації щодо раціонального способу дій учасників конфлікту. Щоб зробити можливим математичний аналіз ситуації без урахування другорядних чинників, будують спрощену, схематизувати модель ситуації, яка називається грою. Гра ведеться за цілком певних правил, під якими розуміється система умов, що регламентує можливі варіанти дій гравців; обсяг інформації кожної сторони про поведінку іншої; результат гри, до якого приводить кожна дана сукупність ходів.

Результат гри (виграш чи програш) взагалі не завжди має кількісне вираження, але зазвичай можна, хоча б умовно, висловити його числовим значенням.

Хід — вибір одного з передбачених правилами гри дій та його здійснення. Ходи поділяються на особисті і випадкові. Особистим ходом називається свідомий вибір гравцем одного з можливих варіантів дій та його здійснення. Випадковим ходом називається вибір з ряду можливостей, здійснюваний не рішенням гравця, а яким-небудь механізмом випадкового вибору (кидання монети, вибір карти з перетасованої колоди і т. п.). Для кожного випадкового ходу правила гри визначають розподіл ймовірностей можливих результатів. Гра може складатися тільки їх особистих або тільки з випадкових ходів, або з їх комбінації. Наступним основним поняттям теорії ігор є поняття стратегії.

Стратегія — це апріорі прийнята гравцем система рішень (виду «якщо — то»), яких він дотримується під час ведення гри, яка може бути представлена у вигляді алгоритму і виконуватися автоматично.

Метою теорії ігор є вироблення рекомендацій для розумного поведінки гравців в конфліктній ситуації, тобто визначення «оптимальної стратегії» для кожного з них. Стратегія, оптимальна по одному показнику, необов'язково буде оптимальною за іншими.

Ігри можна класифікувати: за кількістю гравців, кількістю стратегій, характером взаємодії гравців, характером виграшу, кількості ходів, станом інформації і т.д. [48][49][50]

Математичні аспекти і пропозиції теорії ігор були викладені в книзі Джона Неймона і Моргенштерна «Теорія ігор і економічна поведінка» в 1944р.

У матричних (антагоністичних) іграх математична модель ігор представляється наступним чином (α, β, А), де А — матриця виграшу (програшу), α-безліч стратегій 1-го гравця, β - безліч стратегій 2-го гравця.

Матриця А являє собою матрицю корисності. Функція корисності U вводиться для того що б вирішити проблему оцінки параметрів мають не числову природу. У цьому випадку якщо

a_i>a_j,

то U(a_i)>U(a_j).

Розглянемо приклад в якому матриця ігор А має вигляд:

α1	18	3	0	2	0
α2	0	5	8	20	0
α3	5	4	5	5	4
α4	5	4	2	25	2
α5	9	5	1	20	1
	β1	β2	β325	β4	min aij

У тому випадку коли обидва супротивники діють раціонально, без помилок застосовується процедура

Для розгляду прикладу по кожному рядку матриці вибирається елемент, потім з отриманого вектора вибирається максимальний елемент.

Процедура максіміна також називається процедурою прийняття рішення по Вальду в умовах конфлікту.

Елементи теорії диференціальних ігор

Різні додатки використовують теорію диференціальних ігор. Один гравець-сторона яка переслідує, інший — сторона яка ухиляється від переслідування сторона (маневрова ціль)

_i=f_i(x_i,u₁,u₂) — закон Коши

Де х — вектор станів, х_i— його елементи,

u₁— вектор управління першого гравця,

u₂— вектор управління другого гравця,

Функція корисності має вигляд:

P= (x_i,u₁,u₂)dt

У цьому випадку раціональні стратегії першого і другого гравців характеризуються наступною системою: