
§7. Собственные векторы и собственные числа линейного оператора
Определение
1. Ненулевой
вектор
![]() называется
собственным
вектором
линейного оператора
называется
собственным
вектором
линейного оператора
![]() ,
если под действием
,
если под действием![]() этот вектор переходит в коллинеарный
ему вектор
этот вектор переходит в коллинеарный
ему вектор![]() ,
т.е.
,
т.е.
![]() или
или
![]()
При этом число
![]() называетсясобственным
числом
оператора
называетсясобственным
числом
оператора
![]() .
.
Займемся теперь вопросом о нахождении собственных векторов и собственных чисел линейного оператора.
Пусть в
![]() φ:
φ:
![]() ,
т.е.
,
т.е.![]() ,
где
,
где![]()
Тогда оператор
![]() можно задать формулами:
можно задать формулами:
 или матрицей
или матрицей
 .
.
Для того, чтобы
![]() был собственным вектором с собственным
числом λ,
был собственным вектором с собственным
числом λ,
нужно чтобы
![]() ,
т.е.
,
т.е.![]()
Подставляя эти формулы в систему (1), получим:
 или
или
 .
.
Полученной системе
(2) должны удовлетворять координаты
собственных векторов и собственные
числа. Эта система однородная,
следовательно, она имеет ненулевое
решение при условии
![]() .
Таким образом:
.
Таким образом:
 .
.
Это
так называемое характеристическое
уравнение
оператора
![]() ,
из которого можно находить собственные
числа
,
из которого можно находить собственные
числа![]() ,
а затем, используя систему (2), находить
собственные векторы, соответствующие
этим
,
а затем, используя систему (2), находить
собственные векторы, соответствующие
этим![]() .
.
Характеристическое уравнение часто записывают в более компактной форме. Преобразуем левую часть:
 .
.
Получим:
![]() - характеристическое уравнение.
- характеристическое уравнение.
Пример:
Найти
собственные векторы и собственные числа
линейного оператора
![]() ,
заданного формулами:
,
заданного формулами:

Решение:
1) Составляем характеристическое уравнение:

2) Для нахождения собственных векторов составляем систему (2):

а) при
![]()

Таким образом,
числу
![]() соответствует семейство свободных
векторов
соответствует семейство свободных
векторов ;
;
б) при
![]()

Значит, собственному
числу
![]() соответствует подпространство
соответствует подпространство
свободных векторов

Ответ:
имеем собственные числа
![]() ;
;![]() и соответствующие семейства свободных
векторов
и соответствующие семейства свободных
векторов .
.
Отметим, что
приведенные рассуждения аналогичны и
для
![]() и
и![]() .
.
Например, в случае
![]() ,
если оператор
,
если оператор![]() задан формулами
задан формулами
 ,
,
то характеристическое
уравнение
![]() имеет следующий вид:
имеет следующий вид:
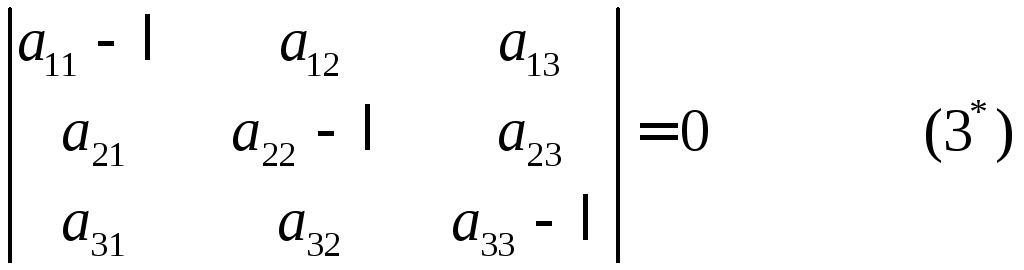 ,
а координаты собственных векторов
,
а координаты собственных векторов
находятся из системы:

