- •Глава 5. Применение производной к исследованию функций
- •§1. Необходимые и достаточные условия возрастания и убывания функции
- •Необходимые условия.
- •Достаточные условия.
- •§2. Экстремумы функции
- •§3. Необходимый признак существования экстремума
- •§4. Первый достаточный признак существования экстремума
- •§5. Второй достаточный признак существования экстремума
- •§6. Выпуклость и вогнутость графика функции
- •§7. Асимптоты графика функции
- •§8. Общая схема исследования функции
- •§9. Наименьшее и наибольшее значение функции на отрезке
- •§10. Решение прикладных экстремальных задач
§9. Наименьшее и наибольшее значение функции на отрезке
Пусть на отрезке
![]() задана непрерывная дифференцируемая
функция
задана непрерывная дифференцируемая
функция
![]() .
Тогда по свойству непрерывной функции
на этом отрезке всегда найдутся такие
точки, в которых функция будет принимать
наибольшее и наименьшее значения.
.
Тогда по свойству непрерывной функции
на этом отрезке всегда найдутся такие
точки, в которых функция будет принимать
наибольшее и наименьшее значения.
Правило нахождения.
-
Находим производную
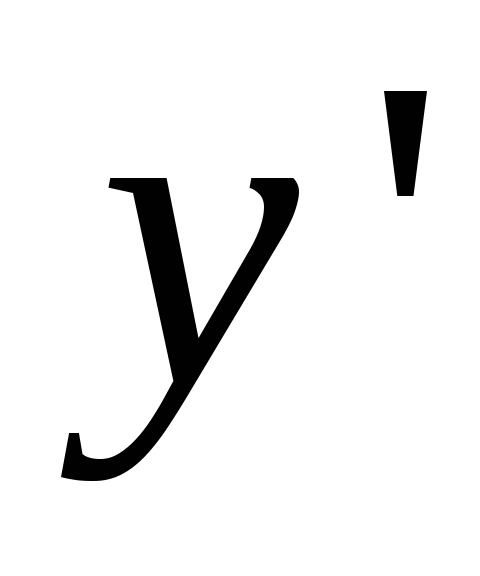 и приравниваем ее к нулю.
и приравниваем ее к нулю.
![]() - критические
точки. Исключаем точки, не входящие в
отрезок
- критические
точки. Исключаем точки, не входящие в
отрезок
![]() .
.
-
Вычисляем значение функции в критических точках, не доказывая вида экстремума.
-
Вычисляем значение функции на концах отрезка.
-
Из всех значений выбираем наименьшее и наибольшее, т.е. находим тотальный максимум и тотальный минимум.
Пример:
Найти
наибольшее
и наименьшее
значения функции
![]() .
.
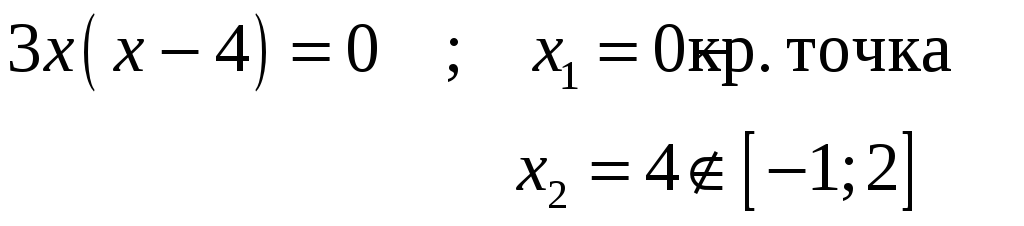 .
.
-
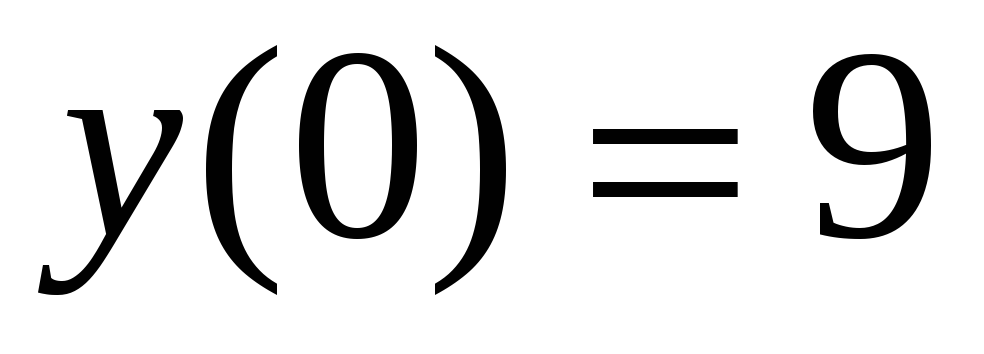 - наибольшее
значение.
- наибольшее
значение. -
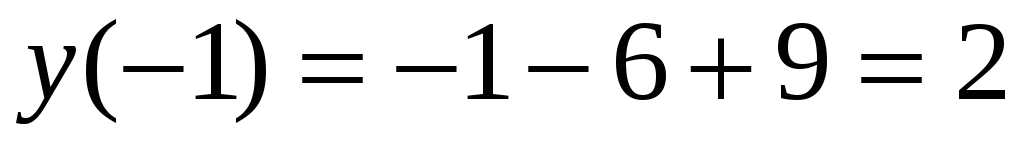
![]()
![]()
![]() - наименьшее
зхначение.
- наименьшее
зхначение.
§10. Решение прикладных экстремальных задач
Если функция
![]() непрерывна на отрезке
непрерывна на отрезке
![]() ,
то она по свойству непрерывных функций
достигает на отрезке
,
то она по свойству непрерывных функций
достигает на отрезке
![]() наибольшее и наименьшее значения.
наибольшее и наименьшее значения.
Если
![]() непрерывна на отрезке
непрерывна на отрезке
![]() и имеет единственный экстремум, то этот
экстремум является наименьшим значением
функции в случае
и имеет единственный экстремум, то этот
экстремум является наименьшим значением
функции в случае
![]() и наибольшим значением в случае
и наибольшим значением в случае
![]() .
.
Практический
интерес имеют не сами
![]() и
и
![]() функции,
а те значения аргумента, при которых
они достигаются. При решении прикладных
задач возникает дополнительная трудность
составления функции, описывающей
рассматриваемое явление или процесс.
функции,
а те значения аргумента, при которых
они достигаются. При решении прикладных
задач возникает дополнительная трудность
составления функции, описывающей
рассматриваемое явление или процесс.
Схема решения прикладных задач.
-
По условию задачи вводим независимую переменную величину
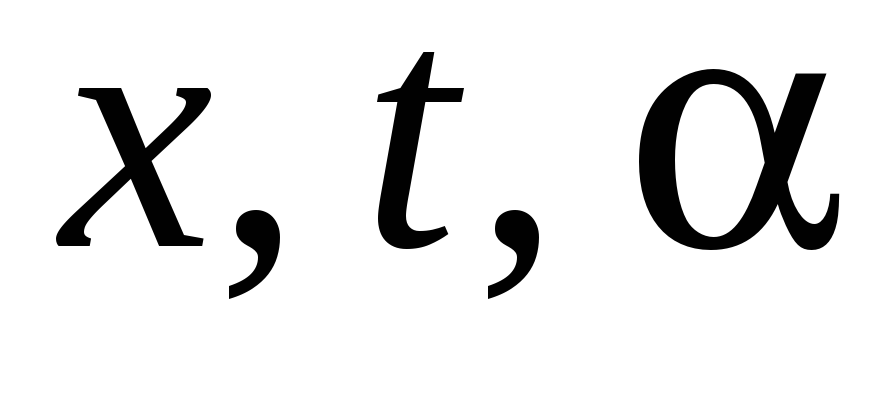 и т.д.
и т.д.
-
Составляем функцию, зависящую от введенного аргумента и описывающую данное явление.
-
По условию задачи находим интервал изменения аргумента.
-
Исследуем функцию на наибольшее и наименьшее значение на заданном интервале.
П ример:
Резервуар,
открытый сверху, имеет форму прямоугольного
параллелепипеда с квадратным дном.
Каковы должны быть размеры резервуара,
чтобы на его лужение пошло наименьшее
количество материала, при условии, что
он должен вмещать 108 куб. л. воды.
ример:
Резервуар,
открытый сверху, имеет форму прямоугольного
параллелепипеда с квадратным дном.
Каковы должны быть размеры резервуара,
чтобы на его лужение пошло наименьшее
количество материала, при условии, что
он должен вмещать 108 куб. л. воды.
![]() - прямоугольный
параллелепипед.
- прямоугольный
параллелепипед.
![]()
![]()
Решение.
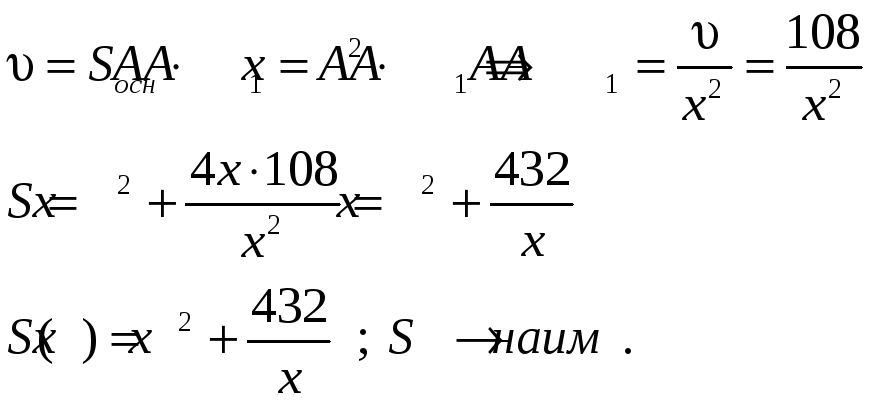
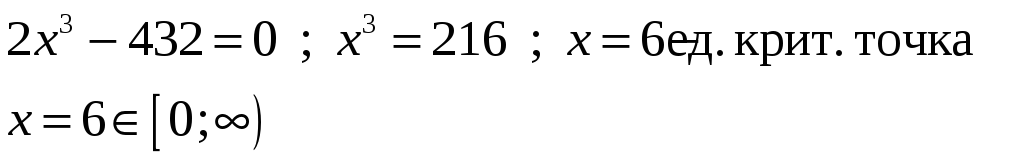
-
х
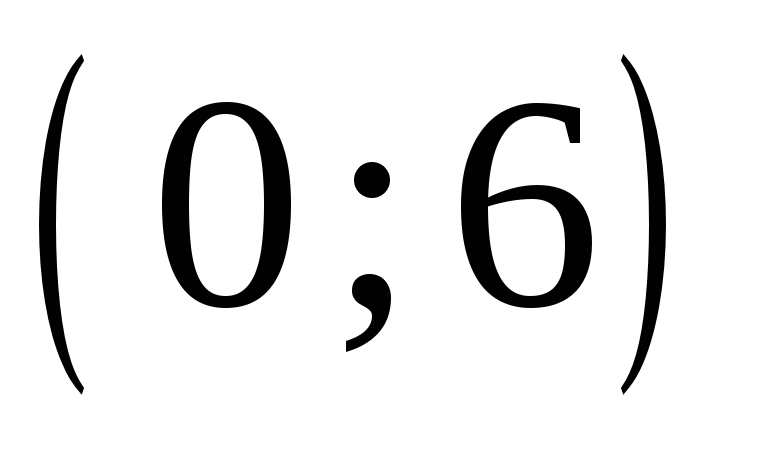
6
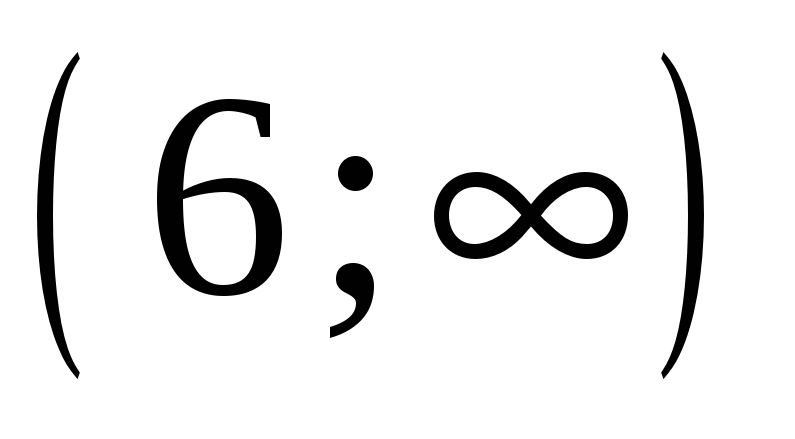
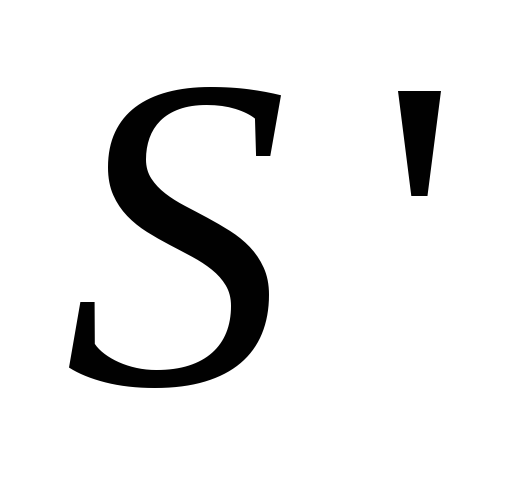
-
0
+
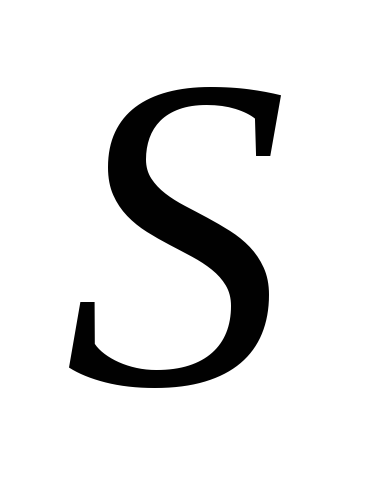

при х = 6 площадь принимает наименьшее значение.
![]()
Вывод:
При стороне
основания АВ
= 6 и высоте
параллелепипеда
![]() на лужение резервуара пойдет наименьшее
количество материала. Чтобы такой
резервуар имел наименьшую поверхность,
высота резервуара должна быть в два
раза меньше стороны квадратного
основания.
на лужение резервуара пойдет наименьшее
количество материала. Чтобы такой
резервуар имел наименьшую поверхность,
высота резервуара должна быть в два
раза меньше стороны квадратного
основания.
![]()