Дифференциальные уравнения с разделяющимися переменными.

Это дифференциальные уравнения вида:

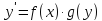
или

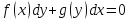
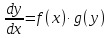
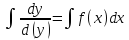
Проинтегрировав, найдем y.

Пример.

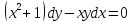
Решение:

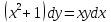
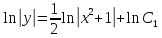
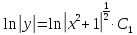
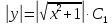
Пусть

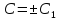
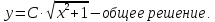
Однородные дифференциальные уравнения первого порядка.

Это дифференциальные уравнения вида:

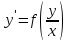
Решается заменой

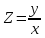
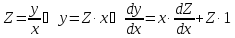
Подставим в исходное уравнение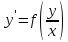, получим

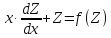
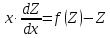
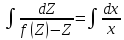
Проинтегрировав, найдем функцию Z, а затем функцию y.

Пример.

Решение:

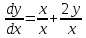
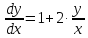
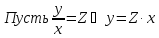
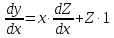
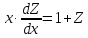
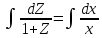
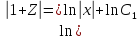
Пусть

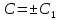
Тогда 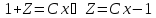, так как

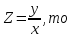
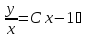
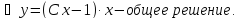
Линейные дифференциальные уравнения первого порядка.

Это дифференциальные уравнения вида:

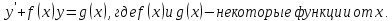
Решается подстановкой:

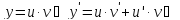
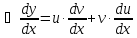
Подставим полученное в уравнение :

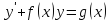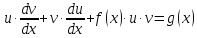
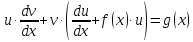
Подставив в равенство 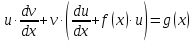значение функцииu, получим дифференциальное уравнение с разделяющимся переменными, решив которое, найдем функцию v, а затем и функцию y.

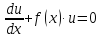
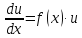
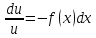
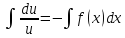
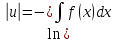
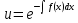
Пример.

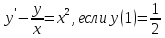
Решение:

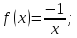
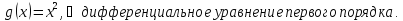
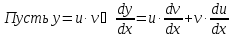
Подставим в уравнение ,

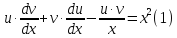
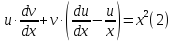
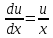
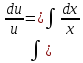
Подставим значения uв равенство (2), получим:

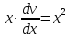
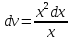
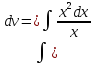
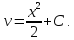
Тогда,

Так как при x=1, , то подставив в общее решение, получим:

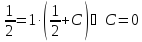
Подставим значение Cв общее решение, получим:

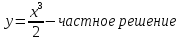
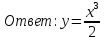
Проверка:

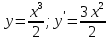
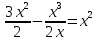
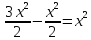
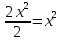
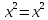
Дифференциальные уравнения второго порядка, допускающие понижение порядка.

Иногда решение дифференциальных уравнений второго порядка можно свести к последовательному решению двух дифференциальных уравнений первого порядка. Тогда говорят, что дифференциальное уравнение допускает понижение порядка.

Это дифференциальные уравнения вида:

или

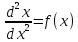
Пример 1.

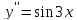
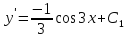
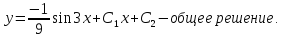
Пример 2.

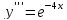
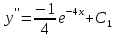
Уравнения этого типа решаются заменой переменной 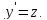Следовательно,

Подставим в дифференциальное уравнение .

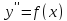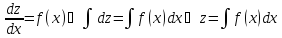
Подставив значение zв дифференциальное уравнение 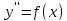, найдем функциюy.

Пример.

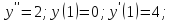
Решение:

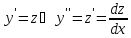
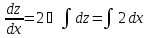
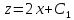
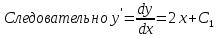
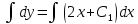
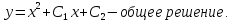
Так как при x= 1, y = 0 и при x = 1, 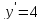, то

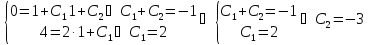
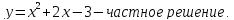
Ответ:.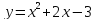

Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами.

Это дифференциальные уравнения вида:

При 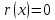получим линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами:

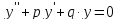
Для его решения составим характеристическое уравнение:

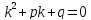
При его решении возможны следующие три случая:

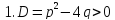
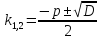
Общее решение дифференциального уравнения второго порядка находим по формуле:

2. ЕслиD=0, то общее решение находится по формуле:

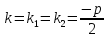
Тогдаобщее решение дифференциального уравнения находим по формуле:

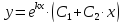
3. 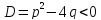, то корни комплексно - сопряженные.

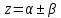
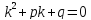
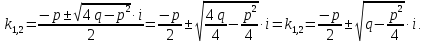
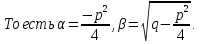
Тогда общее решение находится по формуле:

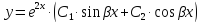
Пример 1.

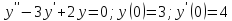
Решение:

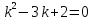
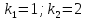
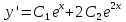
При

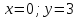
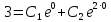
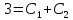
При

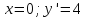
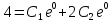
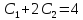
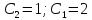
Ответ:

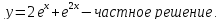
Пример 2.

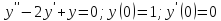
Решение:

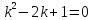
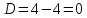
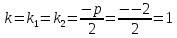
2 способ:

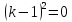
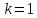
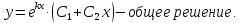
При

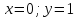
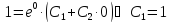
При

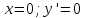
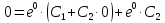
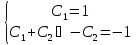
Ответ: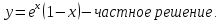

Пример 3.

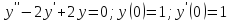
Решение:

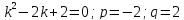
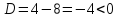
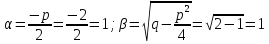
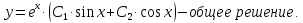
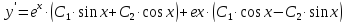
При

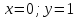
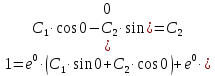
Ответ: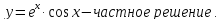

Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами и правой частью специального вида.

Рассмотрим линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами:

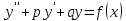
Теорема. Общее решение неоднородного дифференциального уравненияравняется сумме общего решения соответствующего однородного дифференциального уравненияyи частного решения неоднородного уравнения.

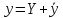
Для дифференциального уравнения второго порядка, у которого правая часть имеет специальный вид, применяются методы подбора формы записи частного решения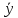по виду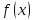,а затем метод неопределенных коэффициентов.

Возможны следующие виды :

1. Если 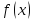многочленn ‒ й степени.

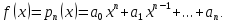
где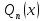‒ многочлен, той же степени, что и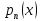, но с неопределенными коэффициентами (A, B, C, D…), r‒ число корней характеристического уравнения, равных нулю, то есть r= 0, или r= 1, или r= 2.

Пример.

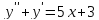
Решение:

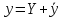
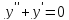
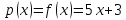
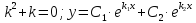
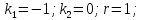
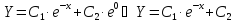
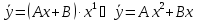
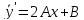
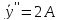
Подставим в исходное уравнение.

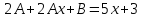
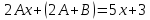
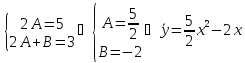
2. Если правая часть уравнения 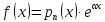, где α ‒ любое число, тогда

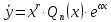, где r ‒ число корней характеристического уравнения, равных α, то есть r= 0, или r= 1, или r= 2.

В частном случае 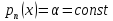, то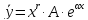, гдеA‒неопределенный коэффициент.

Пример.

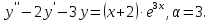
Решение:

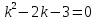
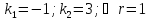
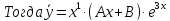
3. Если 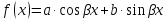,a и b‒ действительные числа.

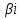,где r ‒ число корней характеристического уравнения, совпадающих с(еслиD< 0) и r= 0(если D≥ 0).

Пример.

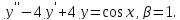
Решение:

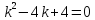
D= 0

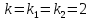
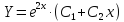
Ответ: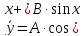.