
- •Лекция № 1.
- •Вопрос 1. Основные сведения о матрицах.
- •Виды матриц
- •Вопрос 2. Операции над матрицами и их свойства.
- •Теорема Лапласа
- •Вопрос 2. Свойства определителей.
- •Лекция № 3
- •Лекция № 4
- •Вопрос 1. Системы линейных алгебраических уравнений слу (Основные понятия и определения).
- •Вопрос 2. Методы решения систем линейных уравнений.
- •1) Метод обратной матрицы (матричный метод) решения систем n линейных уравнений с n неизвестными.
- •2) Правило Крамера решения систем n – линейных уравнений с n – неизвестными.
- •Формулы:
- •Лекция № 5
- •Вопрос 1. Метод Гаусса решения систем линейных уравнений.
- •Алгоритм метода Гаусса:
- •Вопрос 2. Исследование систем линейных уравнений.
- •Лекция № 6
- •Вопрос 1. Системы линейных однородных уравнений.
- •Лекция № 7
- •Вопрос 1. Модель Леонтьева многоотраслевой экономики.
- •Модель Леонтьева многоотраслевой экономики (модели межотраслевого баланса)
- •Балансовые соотношения
- •Линейная модель многоотраслевой экономики
- •Лекция № 8
- •Вопрос 1. Векторы (основные понятия и определения).
- •Вопрос 2. Линейные операции над векторами.
- •Свойства:
- •Вопрос 3.
- •Вопрос 4. Формулы для нахождения длины вектора, расстояния между точками и угла между векторами.
- •Лекция № 9
- •Вопрос 1. Векторное произведение векторов
- •Геометрический смысл.
- •Свойства векторного произведения.
- •Вопрос 2. Выражение векторного произведения через координаты.
- •Вопрос 3. Смешанное произведение векторов
- •Геометрический смысл
- •Вопрос 4. Выражение векторного и смешанного произведения через координаты перемножаемых векторов.
- •Вопрос 5. Уравнение плоскости, проходящей через три данные точки.
- •Лекция № 10
- •Вопрос 1. Понятие векторного (линейного) пространства.
- •Вопрос 2. Размерность и базис векторного пространства.
- •Вопрос 3. Линейная оболочка и ее свойства.
- •Свойства линейной оболочки
- •Вопрос 4. Евклидово пространство.
- •Вопрос 5. Ортогональный и ортонормированный базис.
- •Вопрос 6. Переход к новому базису.
- •Лекция № 11
- •Вопрос 1. Линейные операторы.
- •Вопрос 2. Собственные векторы и собственные значения линейного оператора (матрицы).
- •Вопрос 3. Квадратичные формы.
- •Лекция № 12
- •Вопрос 1. Линейная модель обмена (международной торговли).
- •Лекция № 13
- •Вопрос 1. Уравнения прямой (различные виды). Параметрические уравнения прямой.
- •Уравнение прямой проходящей через две данные точки
- •Угловой коэффициент прямой. Уравнение прямой, проходящей через данную точку с данным угловым коэффициентом.
- •Уравнение прямой, проходящей через данную точку с данным нормальным вектором (нормалью).
- •Общее уравнение прямой.
- •Вопрос 2. Формула угла между прямыми.
- •Вопрос 3. Условия параллельности и перпендикулярности прямых.
- •Вопрос 4. Формула расстояния от точки до прямой.
- •Лекция № 16
Угловой коэффициент прямой. Уравнение прямой, проходящей через данную точку с данным угловым коэффициентом.
Угловым коэффициентом прямой называется тангенс угла наклона прямой, образованный ею с положительным направлением оси OX.
k=
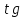 α,
a≠
900
α,
a≠
900
Пусть на прямой даны две точки М1(х1, y1), M2 (х2, y2).
Найдем угловой коэффициент этой прямой. Из ∆М1M2С получим
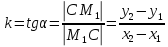
т.е.
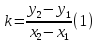
– формула углового коэффициента прямой по координатам.
Заменим точку М2(x, y) на произвольную точку M(x, y) и подставим ее координаты в формулу (1).
Получим:
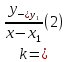
Из формулы (2) следует
y ‒ y1= k × (x ‒ x1)
– уравнение прямой проходящей через данную точку с данным угловым коэффициентом.
Уравнение прямой, проходящей через данную точку с данным нормальным вектором (нормалью).
Нормальным вектором прямой(нормалью) называется любой вектор перпендикулярный данной прямой.
Обозначается
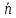 = (a,
b).
= (a,
b).
Пусть
на прямой дана точка М1
(x1,y1)
и дан нормальный вектор прямой
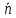 = (a,
b).
= (a,
b).
Пусть М (x, y) произвольная точка прямой.
Тогда
вектор
 перпендикулярен вектору
перпендикулярен вектору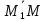 .
Следовательно, их скалярное произведение
.
Следовательно, их скалярное произведение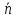 ×
×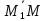 = 0.
= 0.
Запишем это равенство в координатной форме.
Так
как
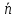 =(а;
b)
и
=(а;
b)
и
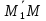 = (x
–x1;
y
–y1),
то равенство
= (x
–x1;
y
–y1),
то равенство
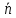 ×
×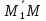 = 0, согласно формуле,
= 0, согласно формуле,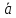 ×
×
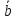 = x1×
x2+
y1×
y2,
в координатной форме примет вид:
= x1×
x2+
y1×
y2,
в координатной форме примет вид:
a· ( x–x1) + b· (y–y1) = 0
– уравнение прямой, проходящей через данную точку с данным нормальным вектором.
Общее уравнение прямой.
Раскроем скобки в уравнении a·(x‒x1)+ b·(y‒y1)=0.
Следовательно, ax ‒ ax1+ by ‒ by1 = 0 или ax + by +(‒ ax1‒ by1) = 0.
Обозначим ‒ ax1 - by1=с,
тогда получим общее уравнение прямой:
ax + by + с = 0
– общее уравнение прямой.
Выразим из общего уравнения прямойyчерез x:

Следовательно,
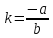
‒ формула углового коэффициента по координатам нормального вектора.
Вопрос 2. Формула угла между прямыми.
Угол
между прямыми:
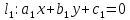 ;
;
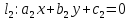 равен углу между их нормальными векторами,
т. е.
равен углу между их нормальными векторами,
т. е.
(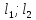 )
=(
)
=(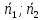 ).
).
Воспользовавшись формулой скалярного произведения векторов, получим:
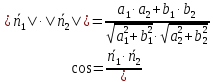
Тогда
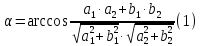
Если прямые заданные уравнениями:
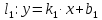 ;
;
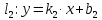 ,
,
тогда
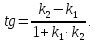
Следовательно,
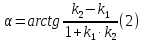
По формулам (1) или (2) находят угол между прямыми.
Вопрос 3. Условия параллельности и перпендикулярности прямых.
Если
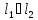 ,
то
= 0. Следовательно,
,
то
= 0. Следовательно,
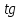
= 0 и
= 0 и
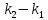 =0.
=0.
Получим:
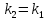
‒ условие параллельности прямых.
Если
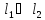 ,
то
=
,
то
=
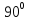 и
и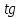
‒ не существует, то есть
‒ не существует, то есть
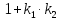 = 0. Следовательно,
= 0. Следовательно,
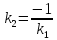
‒ условие перпендикулярности прямых.
Пример:
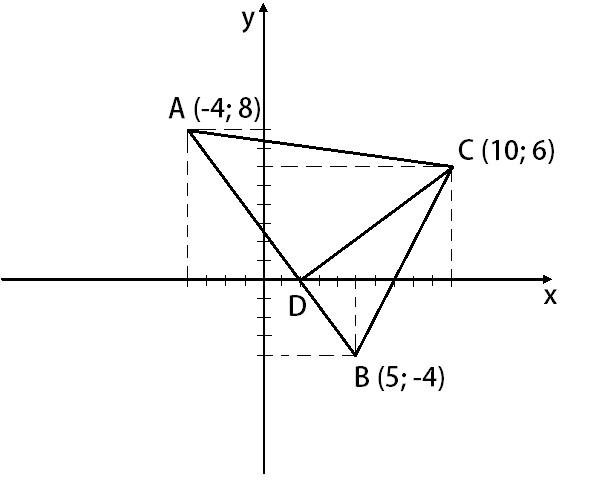
Даны уравнения сторон треугольника
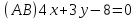 ,
,
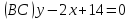 ,
,
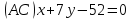 .
.
Найти:
1) Длину │CD│ и уравнение высоты CD.
2) Систему неравенств определяющих треугольник.
3) B.
Решение:
Найдем координаты вершин треугольника.
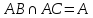
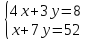
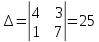
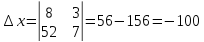
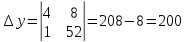
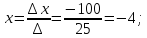
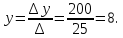
A (– 4; 8)
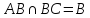
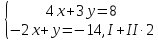
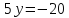
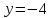 .
.
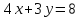
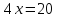
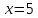
B (5; – 4)
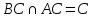
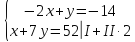
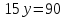
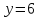
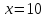
C (10; 6)
1) Найдем уравнение высоты CD.
CD
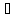 AB
AB
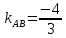 ;
;
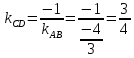 .
.
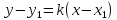
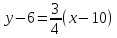 │·
4
│·
4
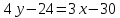
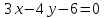 –уравнение
высоты CD.
–уравнение
высоты CD.
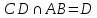
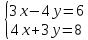
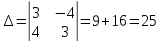
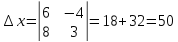
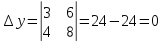
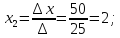
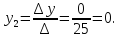
D (2; 0)
Найдемдлину │CD│.
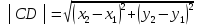
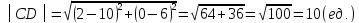
2) Найдем систему неравенств определяющих треугольник.
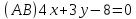 ,
,
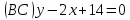 ,
,
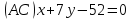 .
.
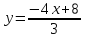 или
или
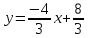 – уравнениеAB.
– уравнениеAB.
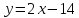 –уравнение
BC.
–уравнение
BC.
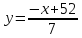 или
или
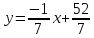 – уравнениеAC.
– уравнениеAC.
 –система
неравенств определяющих ∆ABC.
–система
неравенств определяющих ∆ABC.
3) Найдем B.
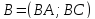
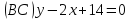 или
или
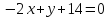
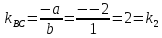
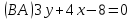
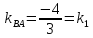
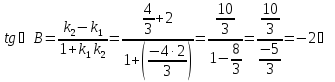
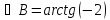
Вопрос 4. Формула расстояния от точки до прямой.
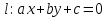 ;
;
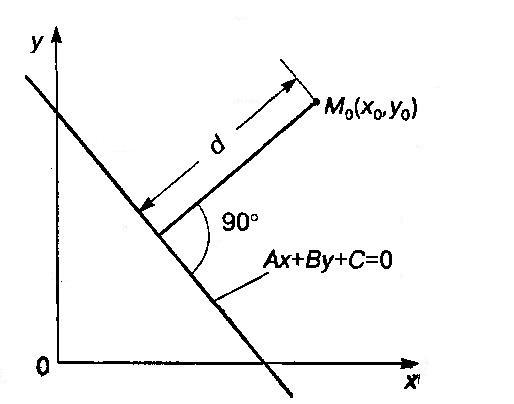
│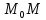 │=
d‒
расстояние
от точки до прямой.
│=
d‒
расстояние
от точки до прямой.
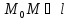
Тогда формула расстояния от точки до прямой примет вид:
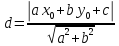
ЛЕКЦИЯ № 14
Вопрос 1. Условия параллельности и перпендикулярности прямых и плоскостей в пространстве.
1) Условие параллельности прямой и плоскости в пространстве.

Пусть
дана плоскость ()
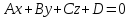 и дан направляющий вектор прямой (
и дан направляющий вектор прямой ( )
)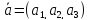 .
.
Если
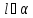 ,
то вектор
,
то вектор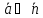 .
Следовательно, их скалярное произведение
.
Следовательно, их скалярное произведение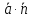 = 0.
= 0.
В координатном виде получим:
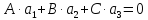
– условие параллельности прямой и плоскости.
2) Условие перпендикулярности прямой и плоскости в пространстве.
Если
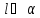 ,
то
,
то
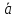 коллинеарен
коллинеарен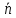 ,
тогда по признаку коллинеарности их
координаты пропорциональны. Следовательно,
получим:
,
тогда по признаку коллинеарности их
координаты пропорциональны. Следовательно,
получим:
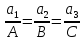
– условие перпендикулярности прямой и плоскости.
Вопрос 2. Уравнение плоскости, проходящей через данную точку, перпендикулярно данному вектору.
Пусть
дана плоскость
и вектор
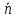 = (A,
B,
C)
= (A,
B,
C)
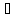 ,
пусть точка
,
пусть точка
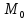 (
(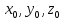 )
ϵ
и точка
)
ϵ
и точка
 произвольная точка плоскости.
произвольная точка плоскости.
Так
как
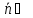 ,
то и
,
то и
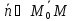 ,
лежащему в плоскости.
Тогда их скалярное произведение
,
лежащему в плоскости.
Тогда их скалярное произведение
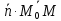 = 0.
= 0.
Запишем это равенство в координатной форме. Получим:
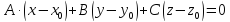
– уравнение плоскости с нормалью.
Вопрос 3. Общее уравнения плоскости. Условия параллельности и перпендикулярности плоскостей.
Раскроем
скобки в уравнении
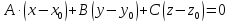 ,
получим
,
получим
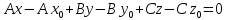
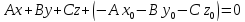
Обозначим:
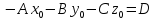
Получим:
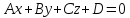
– общее уравнения плоскости.
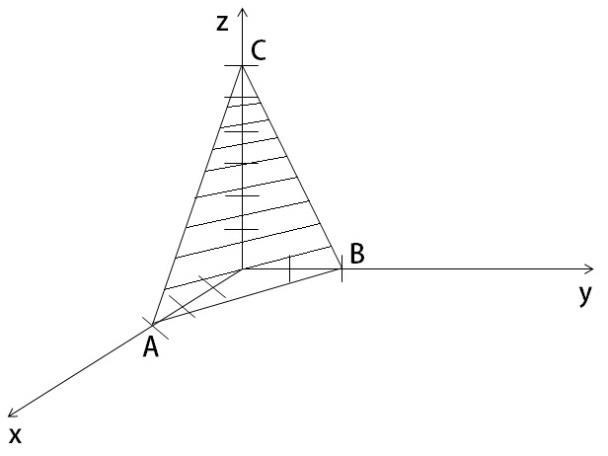
Пример:
Построить
плоскость по ее уравнению
 .
.
При
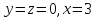 A
(3; 0; 0)
A
(3; 0; 0)
При
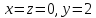 B
(0; 2; 0)
B
(0; 2; 0)
При
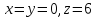 C
(0; 0; 6)
C
(0; 0; 6)
Вопрос 4. Расстояние от точки до плоскости.
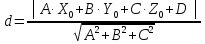
– формула
для нахождения расстояния от точки
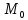 (
(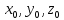 )
до плоскости.
)
до плоскости.
Если
плоскость
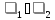 ,
то
,
то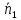 коллинеарен
коллинеарен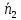 .
Тогда по признаку коллинеарности векторы
пропорциональны.
.
Тогда по признаку коллинеарности векторы
пропорциональны.
Если
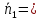 (
(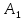 ,
,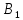 ,
,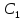 )
и
)
и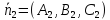 ,
то
,
то
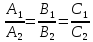
– условие параллельности плоскостей.
Если
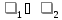 ,
то и
,
то и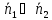 .
Тогда
.
Тогда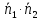 = 0.
= 0.
Следовательно,
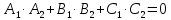
– условие перпендикулярности плоскостей.
Примеры:
1)
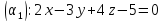
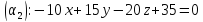
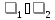 ,
т.
к.
,
т.
к.
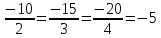 ;k
= –
5.
;k
= –
5.
2)
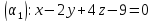
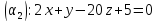
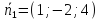
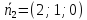
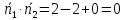 =>
=>
ЛЕКЦИЯ № 15
Вопрос 1. Кривые второго порядка.
К кривым второго порядка относятся: окружность, эллипс, гипербола, парабола.
Кривыми
второго порядка называются линии,
уравнение которых могут быть записаны
в виде
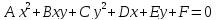 ,
где
,
где
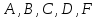 некоторые действительные числа,
называемыекоэффициентами
уравнения,
и, по крайней мере, один из коэффициентов
некоторые действительные числа,
называемыекоэффициентами
уравнения,
и, по крайней мере, один из коэффициентов
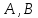 или
или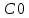 .
.
1) ОКРУЖНОСТЬЮ называется множество точек плоскости, равноудаленных от одной точки, называемой центром окружности.
а) Окружность с центром в начале координат.
По
теореме Пифагора
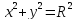
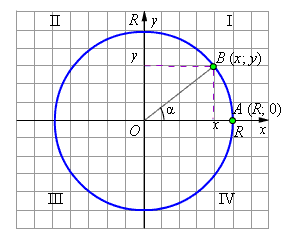
б) Окружность с центром в произвольной точке A1 (x0, y0).
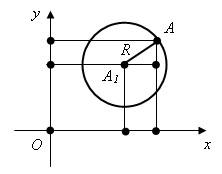
По теореме Пифагора получим уравнение окружности с центром в произвольной точке:
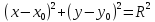
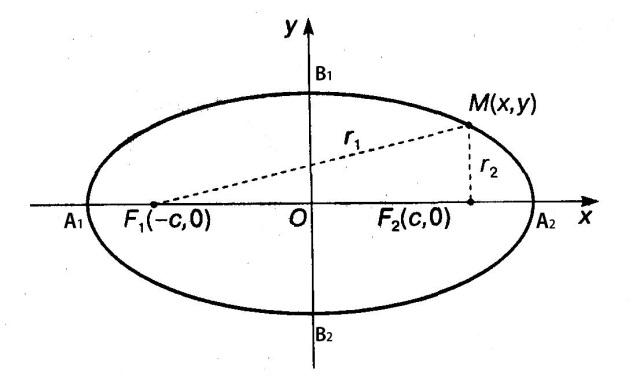
2) ЭЛЛИПСОМ называется множество точек плоскости, сумма расстояний от каждой из которых до двух данных точек, называемых фокусами, есть величина постоянная, причем большая, чем расстояние между фокусами.
Из определения эллипса следует:
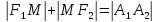
– расстояние между точками.
Введем
обозначения
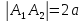 – большая ось эллипса;
– большая ось эллипса;
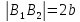 –малая
ось эллипса,
–малая
ось эллипса,
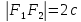 –расстояние
между фокусами,
–расстояние
между фокусами,
где
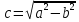 .
.
Тогда получим координаты вершин и фокусов эллипса:
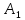 (‒a;
0)
(‒a;
0)
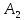 (a;
0)
(a;
0)
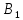 (0;
b)
(0;
b)
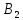 (0;
‒b)
(0;
‒b)
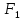 (‒c;
0)
(‒c;
0)
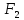 (c;
0)
(c;
0)
Подставив
полученные координаты в формулу
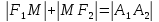 ,
и воспользовавшись формулой расстояния
между точками
,
и воспользовавшись формулой расстояния
между точками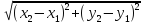 ,
и выполнив необходимые преобразования,
получимканоническое
уравнение эллипса
с центром в начале координат:
,
и выполнив необходимые преобразования,
получимканоническое
уравнение эллипса
с центром в начале координат:
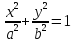
Эксцентриситетом
эллипса
называется отношение половины расстояния
до фокуса к половине большой оси,
обозначается
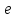 :
:
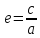 <
1;
<
1;
У
эллипса 0
<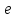 <
1.
<
1.
У
окружности
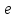 =
0, поэтому эксцентриситет
=
0, поэтому эксцентриситет
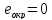 .
.
3) ГИПЕРБОЛОЙ называется множество точек плоскости, модуль разности расстояний от каждой из которых до двух данных точек, называемых фокусами, есть величина постоянная, причем меньшая, чем расстояние между фокусами.
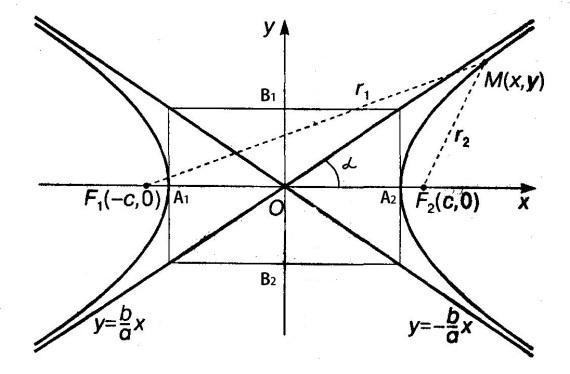
Из определения следует
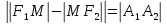
Введем
обозначения
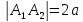 – действительная ось гиперболы;
– действительная ось гиперболы;
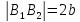 –мнимая
ось гиперболы;
–мнимая
ось гиперболы;
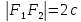 –расстояние
между фокусами,
–расстояние
между фокусами,
где
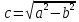 .
.
Тогда получим координаты вершин и фокусов гиперболы:
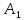 (-a;
0)
(-a;
0)
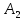 (a;
0)
(a;
0)
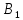 (0;
b)
(0;
b)
 (0;
-b)
(0;
-b)
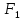 (-c;
0)
(-c;
0)
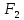 (c;
0)
(c;
0)
Преобразовав
формулу
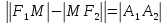 ,
получим (каноническое)
уравнение
гиперболы:
,
получим (каноническое)
уравнение
гиперболы:
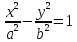
Эксцентриситет
гиперболы:
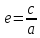 >
1.
>
1.
Уравнения асимптот гиперболы (PL) и (NK):
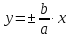 .
.
4) ПАРАБОЛОЙ называется множество точек плоскости, равноудаленных от данной точки, называемой фокусом, и от данной прямой, называемой директрисой.
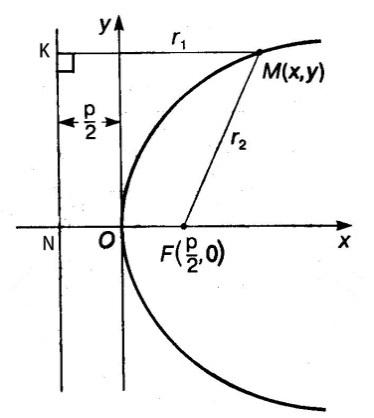
1.
Пусть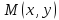 ‒ произвольная точка параболы.
‒ произвольная точка параболы.
Из
определения следует, что расстояние
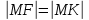
Обозначим
расстояние
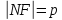 – параметр параболы.
– параметр параболы.
Тогда
ось OYделит
пополам,
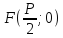 ,
,
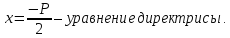
Подставив
в формулу
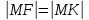 координаты точек и, воспользовавшись
формулой расстояния между двумя точками,
координаты точек и, воспользовавшись
формулой расстояния между двумя точками,
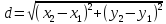 ,
получим:
,
получим:
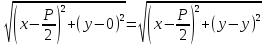
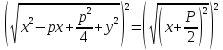
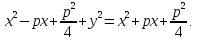
Откуда получим уравнение параболы с вершиной в начале координат (ветви вправо):
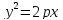
Аналогично выводятся уравнения параболы в остальных трех случаях.
2. Уравнение параболы с вершиной в начале координат (ветви влево).
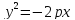
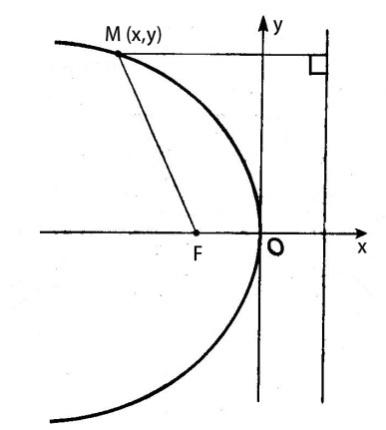
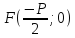 –фокус
–фокус
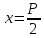 –уравнение
директрисы.
–уравнение
директрисы.
3. Уравнение параболы с вершиной в начале координат (ветви вверх).
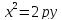
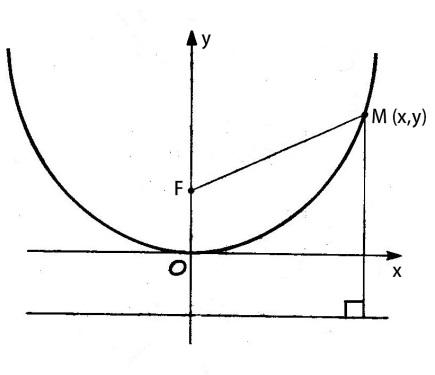
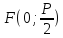 –фокус
–фокус
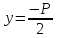 –уравнение
директрисы.
–уравнение
директрисы.
4. Уравнение параболы с вершиной в начале координат (ветви вниз).
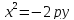
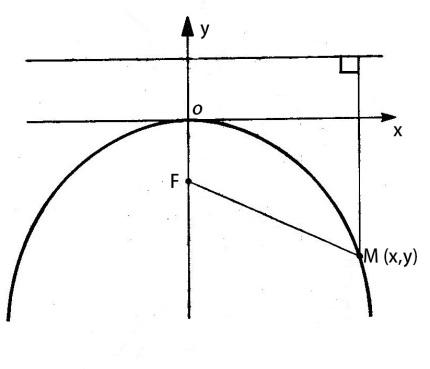
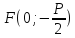 –фокус
–фокус
 –уравнение
директрисы.
–уравнение
директрисы.
