Лекция № 1.

Вопрос 1. Основные сведения о матрицах.

Матрицей размерности m×n называется прямоугольная таблица чисел, состоящая из m– строк и n– столбцов.

Числа, составляющие матрицу, называются ее элементами.

Элемент, стоящий на пересечении строки с номером i(i‒ той строки),

i = 1, 2...m и столбца с номером j(j‒ того столбца),

j = 1, 2…n – обозначается a_ij.

Матрица обозначается заглавными буквами A,B,C…, а их элементы ‒ соответствующими прописными буквами.

A_{m× n}=

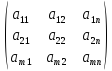
Пример:

A_{3×2 =}

А₁₁ = 3

А₂₁ = – 2

А₂₂ = 5

А₃₂ = –1

Виды матриц

1. Матрица, состоящая из одной строки, называется матрицей ‒ строкой или вектором – строкой. В_1×n= (b₁₁ b₁₂…b_1n)

2. Матрица, состоящая из одного столбца, называется матрицей ‒ столбцом или вектором – столбцом. С_m×1 =

3. Матрица называется квадратной n‒ го порядка, если у нее число строк равно числу столбцов и равноn.

A =– квадратная матрица третьего порядка

Главная диагональ

Элементы квадратной матрицы, у которых совпадает номер строки и столбца, образуют главную диагональ.

Квадратная матрица, все элементы главной диагонали которой равны 1, а остальные элементы равны 0, называется единичной матрицей.

E= – единичная матрица второго порядка.

E= 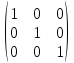– единичная матрица третьего порядка.

Вопрос 2. Операции над матрицами и их свойства.

1.Произведение матрицы на число.

Произведением матрицы A на число λназывается такая матрица B, каждый элемент которой находится по формуле:

b_ij=λ × a_ij

Пример:

A=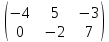

‒ 3A= =

2. Сумма матриц.

Суммой матриц A и B одинаковой размерности называется матрица C, каждый элемент которой находится по формуле: (C_ij= A_ij +B_ij), т.е. матрицы складываются поэлементно.

Пример: + ==

3. Разность матриц.

А ‒ В = А + (‒1) × В

Пример: ‒ ==

4. Произведение матриц.

Произведением матрицы А_m×lна матрицу В_l×nназывается матрица С_m×n, каждый элемент которой c_ijравен сумме произведений всех элементов i – ой строки матрицы A на соответствующие элементыj ‒ того столбца матрицы B.

Пример:

A_2×3= ,А_3×3 =

= =

5. Возведение в степень с натуральным показателем квадратных матриц.

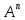= A×A….A

n ‒ раз.

Пример:

A=

= ==

=

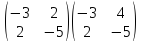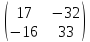
6. Транспонирование матриц.

Матрица А^Т (или А^I) называется транспонированной к матрице A, если строки матрицы A заменены соответствующими столбцами матрицы B, т.е. при транспонировании строки и столбцы меняются местами.

А_3×2 =

=

7. Свойства операций.

1. Коммутативность (переместительный закон)

A + B = B + A; т. е. сумма матриц коммутативна.

A × BB × A; т. е. произведение не коммутативно.

2. Ассоциативность (сочетательный закон)

A + (B + С) = (A + B) + С;

A × (B × С) = (A × B) × С;

3. Дистрибутивность (распределительный закон)

(A + B) × С = A×C + B×C;

4. A × E = A.

ЛЕКЦИЯ № 2.

Вопрос 1. Определители квадратных матриц и способы их вычисления.

Определителем квадратной матрицы называется число, характеризующее эту матрицу.

Определители обозначаются двумя вертикальными чертами:

│A│ или ∆ (дельта).

Определителем первого порядка квадратной матрицы первого порядка A = (а₁₁) называется число, равное элементу этой матрицы.

│а₁₁│= а_11.

Определителем второго порядка квадратной матрицы A = называетсячисло, вычисляемое по формуле:

Пример:

= – 3 × 7 – 6 × (– 5) = – 21+30 = 9.

Определителем третьего порядка квадратной матрицы третьего порядка называется число, вычисляемое по формуле:

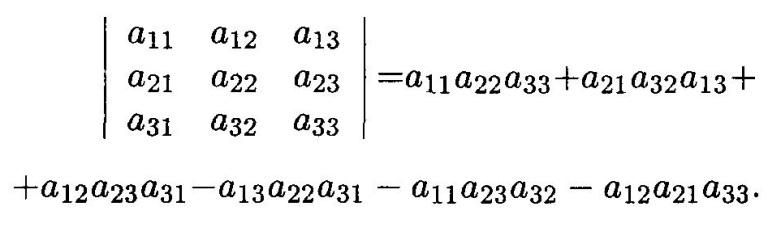
Правило Сарруса (правило треугольника).

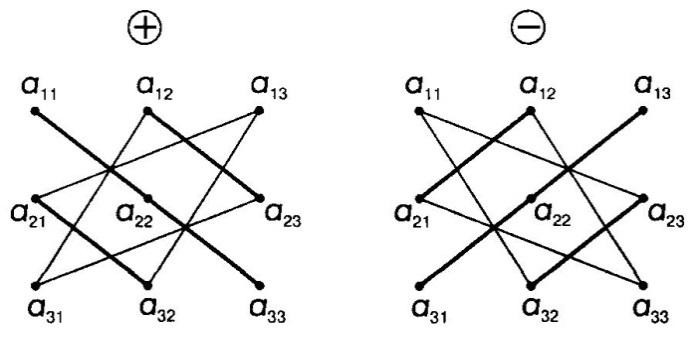
Пример 1:

= – 2×1× (–5) + 5×4×(– 4) + 3×2×(– 3) – (– 3) ×1× (– 4) – 4×2×

(– 2) – 5×3 × (– 5) = 10 – 80 –18 –12 +16 +75 = – 9.

Пример 2:

= 45 + 8 ‒ 24 ‒ 60 + 6 ‒ 24 = ‒ 49.

Минором M_ij элемента a_ijквадратной матрицы n ‒ го порядка называется определитель (n ‒ 1) ‒ го порядка, полу­ченный из данной матрицы вычеркиванием i ‒ й строки и j ‒ го стол­бца, на пересечении которых стоит данный элемент.

Пример:

;

M₁₁ = = 15 + 2 = 17;

M₁₂ = 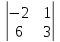= – 6 – 6 = –12; и т. д. всего 9 миноров.

Алгебраическим дополнением A_ijэлемента a_ij квадратной матрицы называется его минор, взятый со знаком (‒1)^i+j.

Пример:

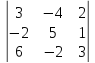
А ₁₁ = (–1)¹⁺¹ × M₁₁ = 17.

А ₁₂ = (–1)¹⁺² × M₁₂ = ‒ 1×M₁₂ = 12.

А ₁₃ = (–1)¹⁺³ × = 4 ‒ 30= – 26; и т.д.