Matlab / Лекция 14

Лекция № 14

Matlab: Символьные вычисления

1. Создание символьных переменных и выражений

2. Символьные операции с выражениями

Система Matlab является самой крупной системой компьютерной математики, ориентированной на матричные и численные вычисления. Однако Matlab имеет также и средства аналитических вычислений. Пакет Symbolic Math Toolbox добавил системе Matlab качественной новые возможности, связанные с выполнением символьных вычислений и преобразований.

С помощью команды:

>> help symbolic

Можно получить перечень входящих в пакет команд и функций. Для получения справки по любой команде или функции можно использовать команду:

>> help sym / name.m,

где name — имя соответствующей команды или функции, а name.m — имя m-файла, задающего данную команду или функцию.

1. Создание символьных переменных и выражений

Команда sym создает символьную переменную и/или выражение. Например, выполнение команды:

x=sym(‘x’)

приведет к созданию символьной переменной .

Если необходимо использовать символьное обозначение для выражения:

,

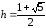тогда команда будет выглядеть:

h=sym(‘(1+sqrt(5))/2’);

Теперь можно использовать в различных математических выражениях. Например:

f=h^2-h-1

вернет:

f = (1/2+1/2*5^(1/2))^2-3/2-1/2*5^(1/2)

Выражение:

f=sym(‘a*x^2+b*x+c’)

придаст символьное выражение 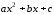переменной 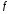. Но и только, Symbolic Math Toolbox не создаст переменных, используемых в данном выражении, а именно 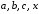. Для дальнейшего осуществления математических операций (таких как интегрирование, дифференцирование, упрощение и т. д.) над функцией 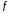, необходимо вручную создать эти переменные:

a=sym(‘a’);

b=sym(‘b’);

c=sym(‘c’);

x=sym(‘x’);

или

syms a b c x;

Рекомендуется использовать syms, что позволит избежать создания избыточных кодов.

2. Символьные операции с выражениями

В Matlab имеется несколько функций для преобразования одной формы представления функции к другой, возможно более простой (табл. 1).

Таблица 1

Символьные операции

Вид преобразования	Ключевое слово	Описание
Приведение подобных слагаемых	collect	Приведение подобных слагаемых полинома
Расширение	expand	Раскрываются суммы и произведения, тригонометрические функции разлагаются по тригонометрическим тождествам
Разложение на множители	factor	Производится разложение выражений или чисел на простые множители.
Упрощение	simplify	Приводит выражение к более простому виду
Обеспечение подстановок	subs

Эти функции в качестве входного параметра могут принимать символьную матрицу. В таком случае выполнение операции происходит поэлементно.

Функция collect(f) представляет 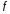как полином от символьной переменной, например , и собирает коэффициенты при степенях . Второй аргумент определяет коэффициенты какой переменной необходимо собрать, если в выражении более одной переменной. Примеры:

f	collect(f)
(x-1)*(x-2)*(x-3)	x^3-6*x^2+11*x-6
x*(x*(x-6)+11)-6	x^3-6*x^2+11*x-6
(1+x)*t + x*t	2*x*t+t

Функция expand(f) расширяет выражение f. Рациональные выражения она раскладывает на простые дроби, полиномы — на полиномиальные разложения и т.д. Примеры:

f	expand(f)
a*(x + y)	a*x+a*y
(x-1)*(x-2)*(x-3)	x^3-6*x^2+11*x-6
x*(x*(x-6)+11)-6	x^3-6*x^2+11*x-6
exp(a+b)	exp(a)*exp(b)
cos(x+y)	cos(x)*cos(y)-sin(x)*sin(y)
cos(3*acos(x))	4*x^3-3*x

Функция factor(f) разлагает выражение f на простые множители, а целые числа — на произведение простых чисел. Если 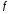не может быть разложен, то результатом выполнения будет само выражение 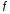. Примеры:

f	factor(f)
x^3-6*x^2+11*x-6	(x-1)*(x-2)*(x-3)
x^3-6*x^2+11*x-5	x^3-6*x^2+11*x-5
x^6+1	(x^2+1)*(x^4-x^2+1)

Функция simplify(f) наиболее мощное средство, она предназначена для алгебраических преобразований, сверток степеней, преобразования тригонометрических, экспоненциальных и логарифмических функций.

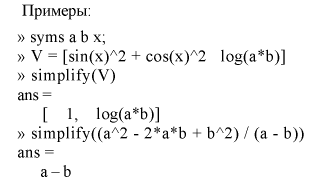
Функция simple(f) использует все правомерные математические способы упрощения для нахождения варианта с наименьшей длиной символьной строки результата. Функция добивается такого результата путем последовательного применения simplify, collect, factor, и других функций упрощения к выражению и сохранением информации о длине строки результата. Возвращает функция наименьший результат (тот ответ, строка которого имеет наименьшую длину).

Функция simple имеет несколько форм записи:

simple(f)

возвращает наименьший результат. Например, выражение:

f = simple(cos(x)^2+sin(x)^2)

вернет f = 1.

Если вы хотите знать каким из методов был получен этот результат, то необходимо использовать вторую форму записи:

[F, how] = simple(f)

В данном виде функция вернет в качестве F наикратчайший результат, а в качестве how — название метода. Например:

[f, how] = simple(cos(x)^2+sin(x)^2)

вернет f = 1

how = combine

Одной из самых эффективных и часто используемых операций символьной математики является операция подстановки. Она реализуется функцией subs, имеющей ряд форм записи:

subs(S) — заменяет в символьном выражении S все переменные их символьными значениями, которые берутся из вычисляемой функции или рабочей области системы MATLAB.

subs(S, NEW) — заменяет все свободные символьные переменные в S из списка NEW.

subs(S, OLD, NEW) — заменяет OLD на NEW в символьном выражении S. При одинаковых размерах массивов OLD и NEW замена идет поэлементно. Если S и OLD — скаляры, а NEW — числовой массив или массив ячеек, то скаляры расширяются до массива результатов.

Примеры:

>>syms a b x y;

>>subs(x-y,y,1)

ans =

x-1

>>subs(sin(x)+cos(y),[x y],[a b])

ans =

sin(a)+cos(b)

7