
Matlab / Лекция 18
.docxЛекция № 18
Matlab: Решение уравнений и их систем
-
Решение уравнений и их систем
-
Решение дифференциальных уравнений и их систем
1. Решение уравнений и их систем
Аналитическое решение уравнений и их систем.



Численное решение
уравнений и их систем. Задача
нахождения корней уравнений встречается
в различных областях научно-технических
исследований. Проблема формулируется
следующим образом. Пусть задана
непрерывная функция
 и требуется найти корень уравнения:
и требуется найти корень уравнения:
 .
.
Будем предполагать,
что имеется интервал изменения

 ,
на котором необходимо исследовать
функцию
,
на котором необходимо исследовать
функцию
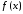 и найти значение
и найти значение
 ,
при котором
,
при котором
 равно или весьма мало отличается от
нуля.
равно или весьма мало отличается от
нуля.
Данная задача в
системе Matlab
может быть решена следующим образом.
Вначале необходимо построить график
функции
 на заданном интервале и убедиться в
существовании корня или нескольких
корней. Затем применить функции поиска
корней.
на заданном интервале и убедиться в
существовании корня или нескольких
корней. Затем применить функции поиска
корней.
Если существует
один корень и график
 пересекает ось
пересекает ось
 ,
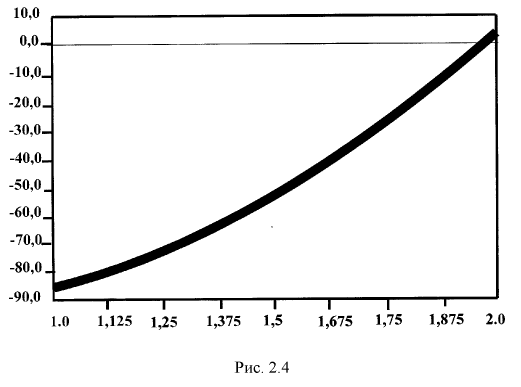
то можно применить функцию:
,
то можно применить функцию:



Если
 имеет больше одного корня и может
касаться и пересекать ось
имеет больше одного корня и может
касаться и пересекать ось
 ,
то следует применить более мощную
функцию
fsolve из пакета
Optimization
Toolbox,
которая решает задачу методом наименьших
квадратов:
,
то следует применить более мощную
функцию
fsolve из пакета
Optimization
Toolbox,
которая решает задачу методом наименьших
квадратов:
fsolve( fun, x0:h:x1),
поиск корней выполняется на интервале от x0 до x1 с шагом h.

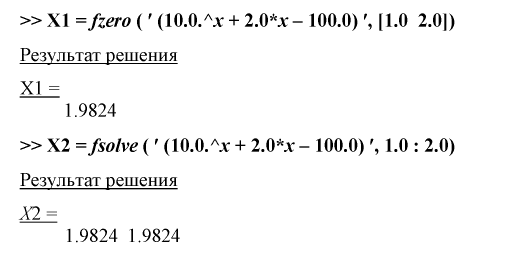

Пример. Численно решить систему уравнений:

В этом случае необходимо создать файл-функцию для расчета значений уравнений от х:
function F = fun_07(x)
F = [2*x(1)-x(2)-2*x(3)+1;
2*x(2)+x(3)-3;
-2*x(1)-2*x(2)+2*x(3)+2];
При этом ввели
вектор x
размерности
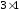 ,
такой что
,
такой что
 .
.
В основной программе делаем вызов функции fun_07 в функции fsolve:
x0=[10;30;-1];
X = fsolve('fun_07',x0)
Решение задачи
определения корней полинома
осуществляется при помощи встроенной
функции roots(v),
где v
— вектор-столбец коэффициентов полинома,
первым элементом которого является
коэффициент при
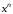 ,
вторым — коэффициент при
,
вторым — коэффициент при
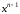 и т. д.
и т. д.
2. Решение дифференциальных уравнений и их систем
Анализ поведения многих систем и устройств в динамике, а также решение многих задач в теории колебаний и в поведении упругих оболочек обычно базируется на решении систем обыкновенных дифференциальных уравнений (ОДУ), или, в оригинале, ordinary differential equations (ODEs). Их, как правило, представляют в виде системы из дифференциальных уравнений первого порядка в форме Коши:
 (1)
(1)
с
граничными условиями
![]() — начальные и конечные точки интервалов.
Параметр t
(независимая
переменная) необязательно означает
время, хотя чаще всего решение
дифференциальных уравнений ищется во
временной области.
— начальные и конечные точки интервалов.
Параметр t
(независимая
переменная) необязательно означает
время, хотя чаще всего решение
дифференциальных уравнений ищется во
временной области.
Система дифференциальных уравнений в форме Коши записывается аналогично (1), но под y в этом случае подразумевается вектор-столбец зависимых переменных. Вектор p задает начальные условия.
Для решения дифференциальных уравнений второго и высшего порядка их нужно свести к системе дифференциальных уравнений первого порядка.
Возможны дифференциальные уравнения, не разрешенные относительно производной:
![]() (2)
(2)
Уравнения (2) аналитически к форме (1) обычно привести не удается.
Однако численное решение особых трудностей не вызывает — достаточно для определения f(y,t) решить (2) численно относительно производной при заданных y и t.
Наряду с ОДУ MATLAB может оперировать с дифференциальными алгебраическими уравнениями (ДАУ, или differential algebraic equations — DAEs). ОДУ и ДАУ являются основой математического моделирования динамических нелинейных (и линейных) систем. Автоматическое их составление и решение реализованы в специальном расширении Simulink.
Аналитическое решение дифференциальных уравнений и их систем.

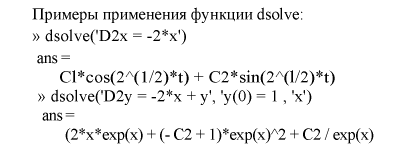
Пример 1.
Аналитически решите дифференциальное
уравнение первого порядка
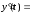
![]() :
:
dsolve('Dy=y*cos(t)+sin(2*t)')
ans =
-2*sin(t)-2+exp(sin(t))*C1
Пример 2.
Аналитически решите дифференциальное
уравнение второго порядка
 :
:
dsolve('m*D2x+H*Dx+k*x=-sqrt(t)')
ans =
-2*m*(2*(-(2*H-2*(H^2-4*m*k)^(1/2))/m)^(1/2)*t^(1/2)*(-(2*H+2*(H^2-4*m*k)^(1/2))/m)^(1/2)*(H^2-4*m*k)^(1/2)+exp(-1/2*(H+(H^2-4*m*k)^(1/2))*t/m)*(-(2*H-2*(H^2-4*m*k)^(1/2))/m)^(1/2)*pi^(1/2)*erf(1/2*(-(2*H+2*(H^2-4*m*k)^(1/2))/m)^(1/2)*t^(1/2))*H-exp(-1/2*(H+(H^2-4*m*k)^(1/2))*t/m)*(-(2*H-2*(H^2-4*m*k)^(1/2))/m)^(1/2)*pi^(1/2)*erf(1/2*(-(2*H+2*(H^2-4*m*k)^(1/2))/m)^(1/2)*t^(1/2))*(H^2-4*m*k)^(1/2)-exp(-1/2*(H-(H^2-4*m*k)^(1/2))*t/m)*(-(2*H+2*(H^2-4*m*k)^(1/2))/m)^(1/2)*pi^(1/2)*erf(1/2*(-(2*H-2*(H^2-4*m*k)^(1/2))/m)^(1/2)*t^(1/2))*H-exp(-1/2*(H-(H^2-4*m*k)^(1/2))*t/m)*(-(2*H+2*(H^2-4*m*k)^(1/2))/m)^(1/2)*pi^(1/2)*erf(1/2*(-(2*H-2*(H^2-4*m*k)^(1/2))/m)^(1/2)*t^(1/2))*(H^2-4*m*k)^(1/2))/(H^2-4*m*k)^(1/2)/(H+(H^2-4*m*k)^(1/2))/(-(2*H+2*(H^2-4*m*k)^(1/2))/m)^(1/2)/(H-(H^2-4*m*k)^(1/2))/(-(2*H-2*(H^2-4*m*k)^(1/2))/m)^(1/2)+C1*exp(-1/2*(H+(H^2-4*m*k)^(1/2))*t/m)+C2*exp(-1/2*(H-(H^2-4*m*k)^(1/2))*t/m)
Пример 3.
Аналитически
решите систему дифференциальных
уравнений
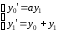 :
:
F=dsolve('Dy0=a*y1','Dy1=y0+y1')
F =
y0: [1x1 sym]
y1: [1x1 sym]
>> F.y0
ans =
C1*exp(1/2*t+1/2*t*(1+4*a)^(1/2))+C2*exp(1/2*t-1/2*t*(1+4*a)^(1/2))
>> F.y1
ans =
1/2*(C1*exp(1/2*t+1/2*t*(1+4*a)^(1/2))+C1*(1+4*a)^(1/2)*exp(1/2*t+1/2*t*(1+4*a)^(1/2))+C2*exp(1/2*t-1/2*t*(1+4*a)^(1/2))-C2*(1+4*a)^(1/2)*exp(1/2*t-1/2*t*(1+4*a)^(1/2)))/a
Численное решение дифференциальных уравнений и их систем. Решение дифференциальных уравнений осуществляют функции ode23 и ode45. Они могут применяться как для решения простых дифференциальных уравнений, так и для моделирования сложных динамических систем.
Известно, что система дифференциальных уравнений может быть представлена в форме Коши:

где
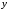 — вектор переменных состояния системы;
— вектор переменных состояния системы;
 — аргумент (обычно время);
— аргумент (обычно время);
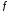 — нелинейная вектор-функция от переменных
состояния
— нелинейная вектор-функция от переменных
состояния
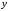 и аргумента
и аргумента
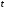 .
.
Обращение к процедурам численного интегрирования дифференциальных уравнений имеет вид:
[t,y]=ode23(‘имя функции’,tspan, y0, options)
[t,y]=ode45(‘имя функции’,tspan, y0, options)
где
имя функции
— строка символов, являющаяся именем
m-файла,
в котором вычисляется вектор-функция
 ,
т. е. в котором находятся правые части
системы дифференциальных уравнений;
,
т. е. в котором находятся правые части
системы дифференциальных уравнений;
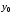 — вектор начальных значений переменных
состояния;
— вектор начальных значений переменных
состояния;
 — массив значений аргумента, соответствующих
шагам интегрирования;
— массив значений аргумента, соответствующих
шагам интегрирования;
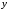 — матрица
проинтегрированных значений фазовых
переменных, в которой каждый столбец
соответствует одной из переменных
состояния, а строка содержит значения
переменных состояния, соответствующих
определенному шагу интегрирования;
tspan
— вектор-строка
— матрица
проинтегрированных значений фазовых
переменных, в которой каждый столбец
соответствует одной из переменных
состояния, а строка содержит значения
переменных состояния, соответствующих
определенному шагу интегрирования;
tspan
— вектор-строка
 ,
содержащая два значения:
,
содержащая два значения:
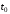 — начальное значение аргумента
— начальное значение аргумента
 ;
;
 — конечное значение аргумента
— конечное значение аргумента
 ;
options
— строка параметров, определяющих
значения допустимой относительной и
абсолютной погрешности интегрирования.
;
options
— строка параметров, определяющих
значения допустимой относительной и
абсолютной погрешности интегрирования.
Для получения решений дифференциальных уравнений в определенные моменты времени можно указать явным образом tspan = [t0, t1, t2, …, tn].
Параметр options можно не указывать. Тогда по умолчанию допустимая относительная погрешность интегрирования принимается равной 1.0е-3, а абсолютная (по каждой из переменных состояния) — 1.0е-6.
Функция ode23 осуществляет интегрирование численным методом Рунге-Кутта 2-го порядка, а с помощью метода 3-го порядка контролирует относительные и абсолютные ошибки интегрирования на каждом шаге и изменяет величину шага интегрирования так, чтобы обеспечить заданные пределы ошибок интегрирования.
Для ode45 основным методом является метод Рунге-Кутта 4-го порядка, а величина шага контролируется методом 5-го порядка.
Пример 4.
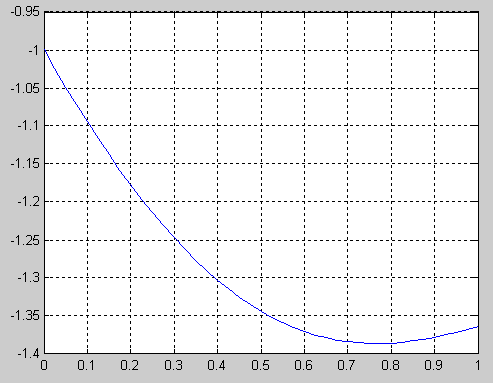
Численно решите дифференциальное
уравнение первого порядка

![]() :
:
tspan=[0 1];
y0=-1;
[T,Y] = ode45('fun_08_1',tspan,y0);
figure
plot(T,Y)
grid on
Содержание файла-функции fun_08_1:
function dy = fun_08_1(t,y)
dy=y*cos(t)+sin(2*t);
Пример 5.
Численно решите дифференциальное
уравнение второго порядка
 .
.
При этом необходимо
преобразовать дифференциальное уравнение
второго порядка в систему двух
дифференциальных уравнений первого
порядка (переход к переменным состояния).
Для этого введем так называемые переменные
состояния
 :
:

Тогда можно записать:
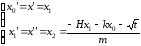
Однако, поскольку в Matlab нумерация индексов массива начинается с 1 (а не с нуля), то систему уравнений необходимо переписать в следующем виде:
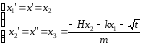
tspan=[0 15];
x0=[0 -10];
[T,X] = ode45('fun_08_2',tspan,x0);
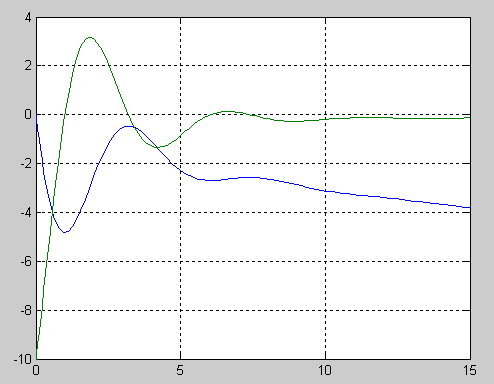
Для наглядного представления результата строится график зависимостей столбцов возвращенной матрицы решений X, от вектора Т:
figure
plot(T,X(:,1),'b',T,X(:,2),'g')
grid on
Содержание файла-функции fun_08_2:
function dx = fun_08_2(t,x)
m=0.5;
H=0.5;
k=1;
dx = zeros(2,1); % создает нулевой вектор-столбец, где будут храниться полученные на данном этапе значения переменных состояния
dx(1)=x(2);
dx(2)=(-H*x(2)-k*x(1)-sqrt(t))/m;
Пример 6.
Решить систему дифференциальных
уравнений:
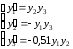 с начальными условиями
с начальными условиями

Для моделирования данной системы, создаем функцию rigid, следующего содержания:
function dy=rigid(t,y)
dy=zeros(3,1);
dy(1)=y(2)*y(3);
dy(2)=-y(1)*y(3);
dy(3)=-0.51*y(1)*y(2);
Решение находится на интервале [0; 12] с начальными условиями [0 1 1]:
[T,Y] = ode45(‘rigid’,[0 12],[0 1 1]);
plot(T,Y(:,1),'-',T,Y(:,2),'-.',T,Y(:,3),'.')

