Matlab / Лекция 17

Лекция № 17

Matlab: Составление функций пользователя

1. Функции, задаваемые пользователем

2. Понятие о файлах-функциях

3. Глобальные переменные

1. Функции, задаваемые пользователем

В пакете Matlab существует три способа задания функций пользователя.

1. Использование команды inline приводит к созданию функции, зависящей от указанных аргументов.

Пример 1. Создание функции одной переменной:

>> f=inline('x^2','x')

f =

Inline function:

f(x) = x^2

>> f(5)

ans =

25

Пример 2. Создание функции нескольких переменных:

>> f=inline('x^2+y^5+sin(z)','x','y','z')

f =

Inline function:

f(x,y,z) = x^2+y^5+sin(z)

>> f(5,6,9)

ans =

7.8014e+003

>> f(0.5,0.6,0.9)

ans =

1.1111

Поскольку большинство функций программы Matlab могут оперировать как векторами, так и скалярами, чтобы быть уверенным, что созданная функция может оперировать с векторами, необходимо использовать поэлементные операции умножения, деления и возведения в степень (.* ./ .^). Таким образом, получается векторизованная версия функции.

Пример 3. Если ставится задача вычислить значения функции в некотором диапазоне значений аргумента, то необходимо использовать поэлементные операции:

>> f=inline('x.^2','x')

f =

Inline function:

f(x) = x.^2

>> f(5:9)

ans =

25 36 49 64 81

%----------------------------------------------------------

>> f=inline('x.^2+y.^5+sin(z)','x','y','z')

f =

Inline function:

f(x,y,z) = x.^2+y.^5+sin(z)

>> f(0:3,0:3,0:3)

ans =

0 2.8415 36.9093 252.1411

2. Использование оператора @ позволяет создавать так называемые анонимные функции. Этот метод является новым в программе Matlab 7, и в настоящее время этому методу отдается предпочтение.

Анонимная (безымянная) функция — в программировании особый вид функций, которые объявляются в месте использования и не получают уникального идентификатора для доступа к ним. Обычно при создании они либо вызываются напрямую, либо ссылка на функцию присваивается переменной, с помощью которой затем можно косвенно вызывать данную функцию.

Пример 4.

>> f=@(x)x.^2

f=

@(x)x.^2

>> f=@(x,y,z) x.^2+y.^5+sin(z);

>> f([1 2],[3 4])

дает значения функции в точках (1, 3) и (2, 4).

3. Задание функции в отдельных файлах (создание файла-функции). Это метод подробно рассмотрим в следующем разделе.

2. Понятие о файлах-функциях

Кроме m-файла сценария, в Matlab существует m-файл функция. Структура m-файла функции имеет вид:

function [Список выходных параметров] = funcname(Список входных параметров)

Текст программы, реализующей алгоритм функции

Выходной параметр 1 = выражение

Выходной параметр 2 = выражение

…

Выходной параметр N = выражение

Правила создания функций пользователя:

1. Файл, содержащий программу реализации функции, должен иметь расширение «m» и называться также как имя функции. Matlab автоматически присваивает данное имя при выполнении команды Save as.

2. Первая строка файла должна содержать описание функции в виде:

function [x1,x2,…,xN] = funcname(param1, param2, ...,paramM);,

где function — ключевое слово; x1,x2,…,xN — переменные, необходимые для сохранения результата функции (выходные параметры функции); param1, param2, ...,paramM — параметры, передаваемые в функцию.

3. Далее следует текст программы, реализующей алгоритм функции. Каждое действие в программе должно быть завершено символом точкой с запятой.

4. В основном файле происходит вызов функции путем упоминания имени, например, если необходимо в переменные y1,y2,…,yN записать результат работы функции:

[y1,y2,…,yN] = funcname(param1, param2, ...,paramM);

Причем, имена возвращаемых переменных и имена параметров функции могут быть разными в основной программе и в функции, главное соблюдать порядок их перечисления.

Функция может вызываться в цикле, например:

for i=1:10;

y(i) = funcname(param1(i), param2(i), ...);

end;

В этом случае param1, param2, ... должны быть векторами соответствующей размерности.

Все переменные, используемые в файле-функции, являются локаль­ными, т. е. действуют только в пределах тела функции.

Файл-функция является самостоятельным программным модулем, который связан с другими модулями и головной программой через входные и выходные параметры. При обнаружении файла-функции он компилируется и затем испол­няется.

Таким образом, пользователь Matlab может сам создавать функции, аналогичные тем, которые входят в этот программный пакет. Создав такую функцию, можно пользоваться ею в среде Matlab, набирая ее имя и параметры в скобках.

Пример 1.

Напишите функцию пользователя, которая возвращает вектор, элементы которого являются значениями функции .

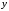Входными параметрами функции должны быть значения переменных и , а также вектор значений моментов времени .

Результат отобразите в виде графика зависимости .

Содержание файла основной программы:

x=5;

y=10;

deltat=0.05;

tk=10;

t=0:deltat:tk;

f=fun_07_1(x,y,t); %вызов функции

figure

plot(t,f)

grid on

Содержание файла-функции fun_07_1:

function [f]=fun_07_1(x,y,t);

f=y^2*t.^3+x*t.^2;

Пример 2. Напишите функцию пользователя, которая возвращает значения функции в дискретных точках .

Входными параметрами функции должны быть значения переменных и , а также дискетные значения переменной .

Результат отобразите в виде графика зависимости .

Содержание файла основной программы:

i=0;

for t=0:deltat:tk;

i=i+1;

f(i)=fun_07_2(x,y,t);

end;

t=0:deltat:tk;

figure

plot(t,f);

grid on;

Содержание файла-функции fun_07_2:

function [f]=fun_07_2(x,y,t);

f=y^2*t^3+x*t^2;

3. Глобальные переменные

Если необходимо чтобы более одной функции использовали некоторую переменную можно объявить ее как глобальную во всех функциях, например:

global XX.

Хотя это не обязательно, но использование больших букв для имени глобальной переменной поможет отличить их от других переменных.

Определение global должно быть до использования самой переменной. Например, создадим m-файл falling.m:

function h = falling(t)

global GRAVITY

h = 1/2*GRAVITY*t^2;

В основном файле или командном окне запишем:

global GRAVITY

GRAVITY = 32;

y = falling((0: .1: 5)' );

Таким образом, строки определения GRAVITY делают ее доступной внутри функции. Можно впоследствии изменить GRAVITY и получить новое решение, не редактируя какие-либо файлы-функции.

7