
- •Физические измерения и обработка их результатов
- •Определение случайных погрешностей прямых измерений Метод Стьюдента
- •Кинематические характеристики равнопеременного движения
- •Порядок выполнения
- •Обработка результатов измерений
- •Точность вычислений
- •Правила округления
- •Контрольные вопросы:
- •Рекомендуемая литература
- •1. Савельев и.В. Курс физики. Т.1. / и.В. Савельев. – м.: Наука, 1989. С. 21-32; 94-97.
Определение случайных погрешностей прямых измерений Метод Стьюдента
В
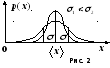
![]()
![]() ,
чем
больше ошибка по абсолютной величине,
тем меньше ее вероятность. Зависимость
плотности распределения вероятностей
измеряемой величины
,
чем
больше ошибка по абсолютной величине,
тем меньше ее вероятность. Зависимость
плотности распределения вероятностей
измеряемой величины![]() от измеренного значения
от измеренного значения![]() описывается кривой (рис. 2), называемой
кривой нормального распределения
Гаусса. Площадь, отвечающая какому-либо
интервалу оси абсцисс, изображает
вероятность попадания случайного
результата в данный интервал. По
распределению Гаусса наиболее вероятным
значением измеряемой величины является
ее среднее значение.
описывается кривой (рис. 2), называемой
кривой нормального распределения
Гаусса. Площадь, отвечающая какому-либо
интервалу оси абсцисс, изображает
вероятность попадания случайного
результата в данный интервал. По
распределению Гаусса наиболее вероятным
значением измеряемой величины является
ее среднее значение.
Вид
кривой распределения определяется
величиной
![]() ,
называемой среднеквадратической ошибкой
(стандартное отклонение):
,
называемой среднеквадратической ошибкой
(стандартное отклонение):
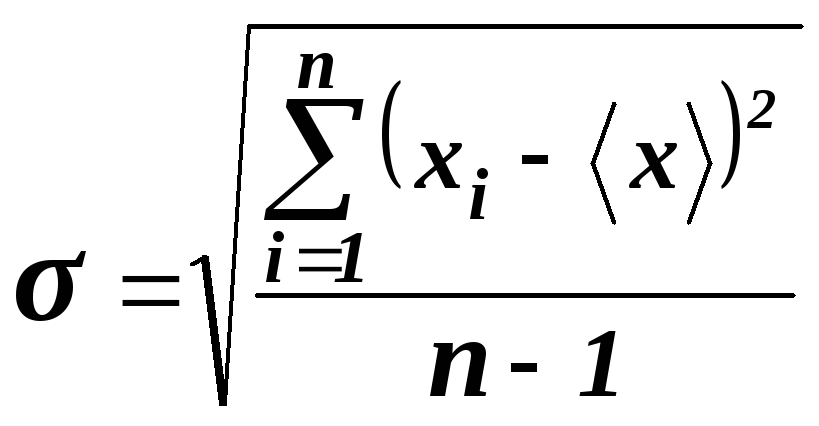 .
.
С
увеличением
![]() точность измерения уменьшается, и кривая
нормального закона распределения имеет
более пологий вид (см. рис. 2).
точность измерения уменьшается, и кривая
нормального закона распределения имеет
более пологий вид (см. рис. 2).
Величина
![]() характеризует разброс отклонений от
среднего значения. На практике число
измерений ограничено (чаще всего не
более 5-7). В этом случае пользуются
распределением Стьюдента.
характеризует разброс отклонений от
среднего значения. На практике число
измерений ограничено (чаще всего не
более 5-7). В этом случае пользуются
распределением Стьюдента.
Английский математик и химик В.С. Госсет (псевдоним Стьюдент) в 1908 г. предложил методику обработки результатов многократных измерений одной и той же величины.
Существуют
специальные таблицы, в которых приведены
коэффициенты
Стьюдента
![]() ,
определяемые доверительной вероятностью
,
определяемые доверительной вероятностью![]() и числом измерений
и числом измерений![]() .
Например, при
.
Например, при![]() для доверительной вероятности
для доверительной вероятности![]() получим
получим![]() (см. таблицу в приложении 1).
(см. таблицу в приложении 1).
Согласно методике Стьюдента средняя квадратическая погрешность результата измерений среднего арифметического определяется формулой:
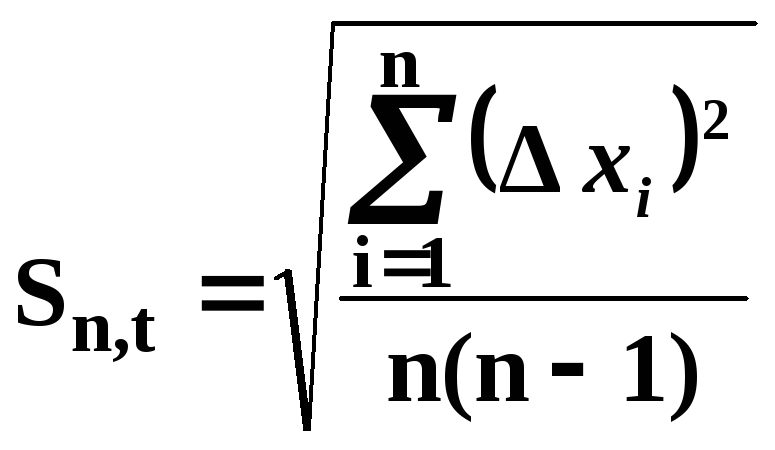 ,
,
где
![]() - абсолютная погрешность каждого
измерения,
- абсолютная погрешность каждого
измерения,
![]() -
число
измерений.
-
число
измерений.
Границы средней квадратической погрешности:
![]() .
.
Абсолютная погрешность измерений:
![]() ,
,
где
![]() – приборная погрешность.
– приборная погрешность.
Если
![]() ,
то
,
то![]() ;
;
если
![]() ,
то
,
то![]() .
.
Окончательный результат записывается в виде:
![]() .
.
Определение погрешностей косвенных измерений
Взять натуральный логарифм от левой и правой частей формулы, помня, что
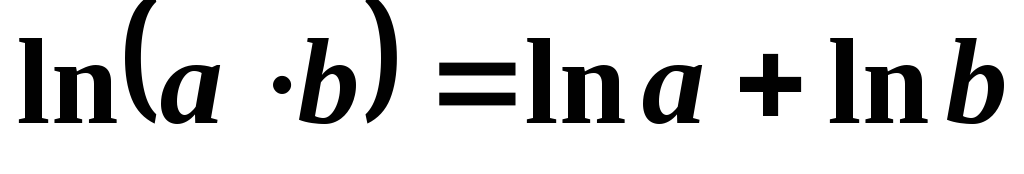 ,
,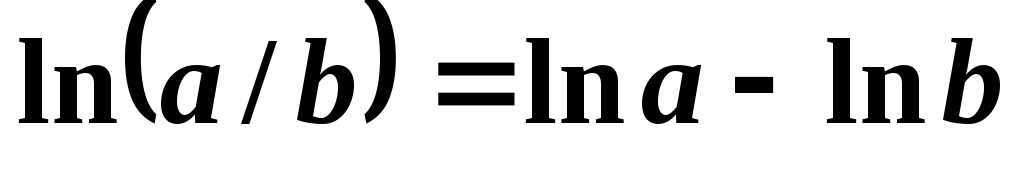 ,
,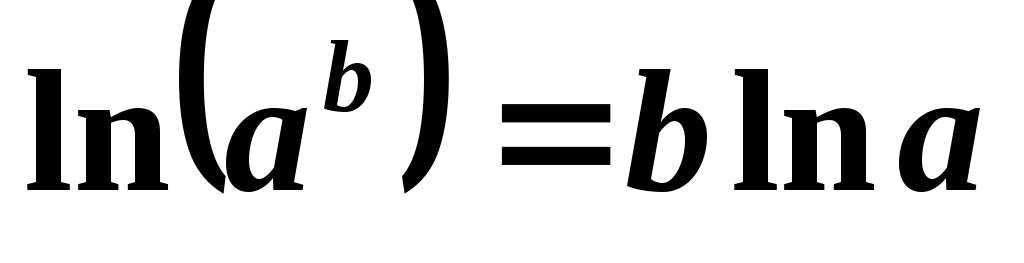 .
.Найти полный дифференциал полученного выражения, помня, что
 .
.Заменить знаки дифференциала
 на
знаки
на
знаки
 .
.Знаки «-», стоящие перед дифференциалами, заменить на знаки «+», так как суммарная погрешность всегда больше погрешности отдельных измерений.
В полученную формулу подставить средние арифметические значения прямо измеренных величин и их абсолютные погрешности.
Вычислить относительную и абсолютную погрешности косвенно измеряемой величины.
Записать окончательный результат в виде
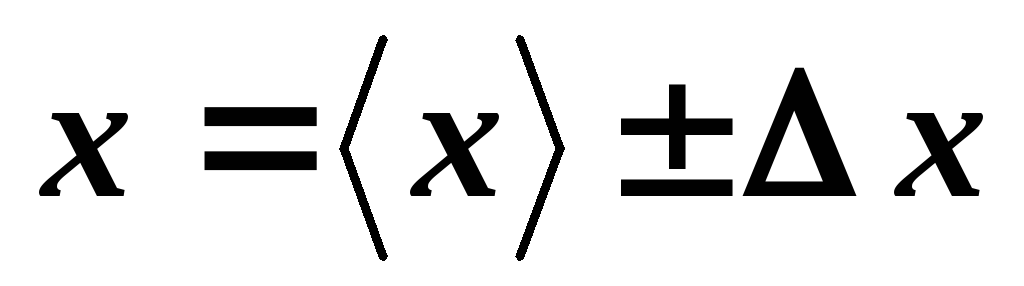 .
.
ПРИМЕР:
Найдём относительную и абсолютную погрешности для ускорения при поступательном движении.
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
![]() -
относительная погрешность величины
ускорения
-
относительная погрешность величины
ускорения
![]() .
.
Абсолютная
погрешность равна
![]() .
.
Окончательный
результат:
![]() .
.
Кинематические характеристики равнопеременного движения
Если
тело, поднятое на высоту
![]() (рис.
3), движется поступательно вниз без
начальной скорости с ускорением
(рис.
3), движется поступательно вниз без
начальной скорости с ускорением![]() ,
то
,
то
![]() .
.
Отсюда
![]() (1)
(1)
Максимальная скорость тела, движущегося без начальной скорости, в нижней точке траектории движения равна:
![]() .
(2)
.
(2)
Максимальная
угловая скорость блока (шкива, оси)
радиуса
![]() :
:
![]() .
(3)
.
(3)
Т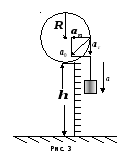 очки,
расположенные на ободе колеса, движутся
с полным ускорением
очки,
расположенные на ободе колеса, движутся
с полным ускорением![]() (см. рис. 3), где
(см. рис. 3), где![]() - тангенциальная составляющая ускорения,
направленная по касательной, равная по
модулю ускорению поступательного
движения тела, т.е.
- тангенциальная составляющая ускорения,
направленная по касательной, равная по
модулю ускорению поступательного
движения тела, т.е.![]() ;
;![]() – нормальная составляющая ускорения,
направленная к центру окружности равная
по модулю
– нормальная составляющая ускорения,
направленная к центру окружности равная
по модулю
![]() .
(4)
.
(4)
Модуль полного ускорения
![]() .
(5)
.
(5)
Угловое
ускорение маховика (блока, шкива) радиуса
![]() :
:
![]() .
(6)
.
(6)
