afanasev_a_e_fizicheskie_processy_torfyanogo_proizvodstva

171

с уменьшением толщины Hi = h сушимого слоя торфа при прочих одинаковых факторах.

Минимальная толщина слоя аэрации Нкр = Ност (см. рис. 4.21 а) вычисляется из формулы

Нкр а τ , (4.83)

Fo

которая зависит от критерия Фурье Fo. Как установлено [10] , оптимальный режим сушки определяется условием: B = max, Pгл = 0:

Hi Hоп 1,41 a τ . (4.84)

Для торфа средней степени разложения численные значения соответ-

ственно равны Н0 = 80-120 мм, Нкр = 20-30 мм, h = 14-20 мм. Причем здесь для низинного торфа меньшие, а для верхового большие значения чисел.

Сокращение продолжительности сушки фрезерного торфа вызвано одновременной сушкой всех слоев фрезерного торфа, только в разной степени, т.е. по мере сушки верхнего подсыхает и нижележащий, поэтому начальная влажность слоя в последующем цикле уменьшается на 1-3%. После сработки 3 – 5 слоев торфа остаток подсушенного торфа фрезеруют с залежью таким образом, чтобы получить начальную толщину аэрированного слоя Hi = H0 = 80-120 мм с влагой меньшей, чем в первом большом цикле, на Δω≈3-5% (большой цикл – это время между двумя ближайшими операциями фрезерования).

При выпадении осадков последние как бы "проваливаются" в нижние слои до границы с залежью, что позволяет значительно раньше (до 30%) начинать цикл сушки по сравнению с существующей схемой добычи.

В приложении 4.10 и на рис. 4.24 показаны соответственно теплофизические характеристики фрезерного торфа и относительное изменение затрат тепловой энергии на испарение i·r/B влаги при сушке торфа в толстых слоях, т.е. при максимальном использовании солнечной энергии i·r/B→1, а при минимальном – i·r/B →0 – резкое уменьшение величины

i·r/B соответствует Hi =Hкр.

При переходе ко 2-му большому циклу можно подсохший слой (остаток) не перемешивать с вновь нафрезерованным слоем, а заложить его с помощью специального устройства между залежью и нафрезерованным слоем – 2-слойная схема сушки [21], что позволяет при меньшей толщине слоя аэрации достичь приблизительно тех же результатов, что и в толстых слоях, но за счет тепловлагоизоляции сырого слоя торфа от влажной торфяной залежи. Продолжительность сушки торфяной крошки в толстых слоях рассчитывается по той же схеме, что и в существующей технологии добычи торфа, только с учетом уменьшения содержания влаги в начале сушки: ωн ωi Δω , где Δω = 1-3%, при отсутствии подфрезеровывания.

172

При 2-слойном расстиле [21] общая толщина слоя Hi<<Но и соответствует толщине торфа, приблизительно равной расстилу при существующей схеме добычи, т.е. hi Hост . Продолжительность сушки τ в этом случае

рассматривается как в однослойном расстиле с удельной загрузкой Рс1 (рис.4.25) (до ворошения), а после ворошения – с удельной загрузкой

Рс = Рс1+ Рс2:

Рис. 4.24. Относительное изменение затрат тепловой энергия на испарение влаги при сушке фрезерного торфа в толстых слоях: 1 – низинный осоковый торф, Rт= 20-25%, Wн = 4,27 кг/кг; т/пр "Озерецкое"; 2 – верховой сосново-пушицевый торф, Rт = 25%, Wн = 2,5 кг/кг; т/пр "Васильевский Мох"; 3 – переходный торф,

Rт = 30%; Wн =5,1 кг/кг; т/пр "Лихославльское"

Эффективная величина коэффициента диффузии влаги аmi (с учетом тепловлагопроводности) определяется из формулы [21] (А.Е. Афанасьев, А.К. Бавтуто)

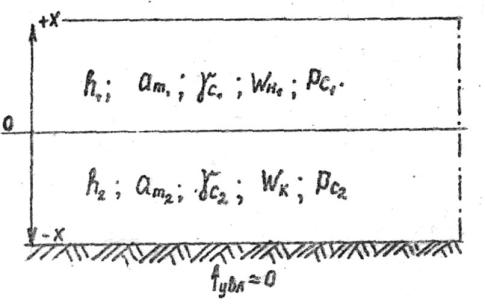
173

где W – изменение влагосодержания за время сушки слоя торфяной крошки, толщина которого меньше зоны испарения. Наиболее приемлемый срок ворошения – достижение влагосодержания Wв1 верхнего слоя, соответствующего второму критическому Wк2, определяемому по формуле ВНИИТП.

Рис. 4.25. Расчетная схема сушки торфяной крошки

вдвухслойном расстиле

4.7.3.Капиллярное давление при сушке частиц крошкообразного торфа

Сушка торфа в полевых условиях связана не только с удалением влаги, но и пропиткой отдельных частиц водой (при выпадении осадков), а также с процессами массопереноса как между частицами в слое торфа, так и с подстилающей влажной залежью. Количество поглощенной воды при выпадении осадков определяется коэффициентом поглощения Кос осадков, а количество удаленной – интенсивностью iс испарения влаги. Эти процессы сопровождаются изменением размеров частиц и пор, общей пористости за счет развивающегося в них капиллярного Рк давления. В торфяной залежи оно измеряется с помощью керамических стержневых пористых датчиков, соединенных с U-образным манометром и предварительно заполненных обезгаженной дистиллированной водой и поставленных в залежь (датчики С.С. Корчунова). Значение давления Рк (или потенциала влаги Ф Рк / ρж , Дж/кг) составляет небольшую величину (Рк< (1…6)·104 Па),

поэтому данный тип датчиков не может быть использован для оценки Рк в отдельных частицах фрезерного торфа или в микрообъемах кускового.

Для этих целей используется метод микротензиметрии [23], который находит все большее распространение в науке и практике.

174

Устройство представляет собой тупиковый (стеклянный или кварцевый) капилляр длиной l = 40-50 мм и внутренним радиусом r0 = 0,1-5,0 мкм, помещенный в исследуемую "точку" частицы (рис. 4.26 а, б).

Капиллярное давление Рк вычисляется по формуле

где Р0 – атмосферное давление, Па; l0, lx – длина незаполненной части капилляра соответственно до постановки его в торф и после, м. Точность метода (приложение 4.11)

ошибка измерения линейного смещения столбика воздуха в капилляре). Поле сил тяжести не учитывается.

Рис. 4.26. Микротензиометр: а - заполнение жидкостью: 1 – сосуд с водой, 2 – микрокапилляр; б – постановка микрокапилляра в частицу торфа 3’’, 3’ – усадка частиц (уменьшение объема), Р0 – барометрическое давление

На графиках lgPк = f(W) для частиц из верхового и низинного торфа диаметром dн = 3-6,5мм обнаружен (рис. 4.27) характерный перегиб, разделяющий процесс структурообразования на два периода [6].

Размеры пор изменяются от D = 16 до 0,2 мкм, а максимальная величина |Рк| приходится на убывающий период интенсивности сушки (рис. 4.28) и достигает 0,8 МПа.

175

Рис. 4.27. Зависимость капиллярного давления от влагосодержания частиц: I, П – периода структурообразования

Высота подъема h жидкости в торфе зависит от гидрофильности твердой фазы, свойств жидкости и радиуса пор (капилляров) и вычисляется из формулы (1.74)

h2σ cos .

ρж g r

Высота подъема h жидкости между двумя параллельными недалеко отстоящими плоскостями определяется по формуле

σ cos hп ρж g d ,

где d – расстояние между плоскостями.

На модели порового пространства – тупиковом капилляре (рис. 4.26 а) – можно изучить процесс водопоглощения ВП, выраженный в относительных единицах объема пор, занятых жидкостью. Для участка П (рис.4.27) выражение для водопоглощения принимает вид

Давление парогазовой смеси в защемленной поре

176

знака, способствующее образованию дефектов и последующему разрушению структуры торфа, т.е. Вп и Ргаз растут с уменьшением радиусов пор, увеличением l и |Рп| при условии, что величина |Рк|>Pд (Pд – давление поля сил тяжести) (см. рис. 4.29 II). Для |Рк|<Pд значение Вп увеличивается с

ростом значений r (при r = 0,1 – 8,0 мкм, Вп = 0,59-0,01, а Ргаз = 246 – 101 кПа). (см. рис. 4.29 III). При |Рк|=Pд величина Вп →min (r = rк≈20 мкм). При

Рк >>> Pд, r → min в узких капиллярах сказываются реологические свойства жидкости (растет предельное напряжение Θ сдвига жидкости, за счет чего резко уменьшается подвижность граничных слоев, заполняющих весь объем капилляра).

Рис. 4.28. Изменение влагосодержания и капиллярного давления в процессе сушки частиц торфа, α const

При полевой сушке намокание торфа сопровождается разрушением и уплотнением (уменьшением размеров пор) частиц торфа под действием удара Ру капель дождя (dк = 0,1-7мм), поэтому выражение для Вп в общем виде должно учитывать не только Рк, Рд , но и величину Ру:

Качественный анализ формулы (4.90) подтверждается данными по водопоглощению фрезерного торфа [10] и согласуется с исследованиями Ю.А. Бермана, И.И. Лиштвана, О.В. Попова, Л.М. Малкова, А.А. Роде и др.

177

Рис. 4.29. Схема заполнения водой тупикового капилляра (водопоглощение объемное – пористое тело полностью погружено в жидкость): I, II, III – возможные периоды заполнения; II – эксперимент Рк>Рд ; III – Рк<Pд при ri=rk , Pк=Рд

4.7.4. Капиллярная пропитка пористых тел

Пропитка коллоидных капиллярно-пористых тел жидкостями – сложный процесс, зависящий от ряда факторов, во многом определяемый размерами и конфигурацией пор, их пространственным расположением. Реальные тела отличает чрезвычайная сложность строения количественного критерия для всесторонней характеристики пористой структуры. Для описания процессов пропитки используются различные модели пористого тела

[14, 24, 25].

При сушке торфа возникают необратимые структурные изменения, которые уменьшают водопоглотительную способность торфяных сорбентов. Необходимо создавать такие материалы, которые бы не меняли или только частично уменьшали свои поглотительные свойства. На практике в сорбционных процессах применяются пористые адсорбенты с различными физико-химическими свойствами. Для описания сложных процессов поглощения жидкости в торфе использована модель пористого тела – совокупность сквозных и тупиковых (см. рис. 4.26) кварцевых капилляров.

Объем жидкости Q, протекающий через цилиндрический капилляр радиусом r и длиной l за время τ, определяется законом Пуазейля:

где η – вязкость жидкости (приложение 4.12); ∆Р – перепад давления на концах капилляра.

Средняя скорость течения жидкости составляет соответственно

Рис.4.30. Схема капилляра (l0 – длина сжатого воздушного столбика в капилляре, l – полная длина капилляра, li – длина заполненного капилляра жидкостью, h – высота поднятия жидкости; α – угол наклона капилляра)

Знак «минус» в (4.100) опущен и указывает на сопротивление Ргаза переносу жидкости. Причем кубический корень возникает за счет противодавления газа в тупиковом капилляре, которого нет в сквозном. Из-за малости не учитывается роль сил инерции жидкости.

В практике, например при намокании торфа, имеют место процессы, связанные с пропиткой тупиковых и квазитупиковых пор. Скорость процесса растворения и диффузионного переноса защемленного газа зависит от размеров и формы образца, физико-химических свойств газов и жидкостей. Она определяет скорость встречного диффузионного потока жидкости в глубь образца. В процессе пропитки можно выделить две стадии: быструю, скорость которой определяется вязким сопротивлением жидкости, и медленную, диффузионную. Диффузионная стадия пропитки контролируется диффузионным сопротивлением, однако описывается тем же зако-

180

ном, что и быстрая стадия процесса. На скорость диффузионной пропитки радиус капилляра не влияет.

Для ускорения пропитки капиллярно-пористых тел могут быть использованы широко применяемые в настоящее время поверхностноактивные вещества. Обладая способностью изменять поверхностное натяжение жидкости и краевой угол смачивания Θ, ПАВ влияют на глубину и скорость капиллярной пропитки. Рассматривая процесс впитывания растворов ПАВ в единичные гидрофобизованные кварцевые капилляры, авторы работ [24, 25] пришли к выводу, что кинетика процесса описывается уравнением Уошборна.

Экспериментальное подтверждение зависимостей (4.96) и (4.100) было выполнено на сквозных и тупиковых капиллярах с внутренним диаметром 8... 12 мкм растворами различной кислотности (рН = 4,2... 10,3) при температуре Тс = 293 К и влажности воздуха φ = 0,6...0,7; рН - задавалась с помощью растворов NаС1, СН3-СООН, Nа2СО3. Линейные перемещения мениска определялись с помощью компоратора ИЗА-2.

Анализ графиков l = f(τ) (рис. 4.31, 4.32) показывает, что пропитка кварцевых капилляров растворами различной кислотности начинается с момента соприкосновения капилляра с раствором, а сами зависимости

l = f( τ ) и l = f( 3 τ ) линейны и константы пропитки имеют постоянные значения на протяжении всего процесса впитывания. Это свидетельствует о том, что процесс впитывания протекает в соответствии с законом капиллярной пропитки. В процессе поглощения жидкости выделяются две стадии, которые сменяют друг друга: быструю (τ ~ 20 с) и медленную (τ > 20 с) –диффузионную, определяемые соотношениями (4.96) и (4.100) при

τ >0.

Установлено, что для капилляров с большой площадью поперечного сечения характерна большая скорость подъема жидкости. В то же время максимальная высота подъема и необходимое для этого время меньше, чем в случае более тонких капилляров.

При поглощении растворов кислой среды процесс протекает быстрее, чем в щелочной. Зависимость констант сорбции k2 от рН тупиковых капилляров такая же, как и у сквозных, то есть уменьшается с увеличением рН (рис.4.33) и определяется уравнением