14.3. Операторные характеристики и канонические схемы цифровых фильтров

В главе J при рассмотрении способов представления сигналов и характеристик цепей было показано, что в дискретном случае преобра­зованию Лапласа, переводящему функции времени х (t) в X (p), соот­ветствует z-преобразование, переводящее x(kT) в Х(z), где z = e^pT. Физически оператору z^-1=e^-pT соответствует задержка сигнала на время Т .

Применим z-преобразование к разностному уравнению (14.7):

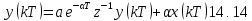Соответствующая выражению (14.14) схема приведена на рис. 14.5. Применяя к этой схеме правило определения передаточной функции цепи с обратной связью, найдем:

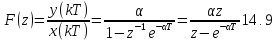
Функция (14.9) и схема, приведенная на рис. 14.5, представляют собой фильтр первого порядка. Функция F(z) является рациональной дробью относительно г и называется системной или пере­даточной функцией фильтра. Более сложные фильтры имеют и более сложные характеристики.

В общем по аналогии с F (р) функцию F (z) можно представить в виде

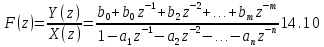
По аналогии с каноническими схемами передающих цепей, рас­смотренными в § 2.24, составим каноническую схему цифрового (дис­кретного) фильтра третьего порядка (рис. 14.6) с характеристикой

Для пояснения ее действия введем промежуточную переменную U. Из условия равновесия для левого сумматора найдем:

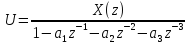
Выход Y (z) в свою очередь равен U (). Отсюда F (z)= Y (z)/X (z) дает выражение (14.11).

Очевидно, что для построения цифровых фильтров могут быть ис­пользованы и другие канонические схемы, и, в частности, схемы кас­кадного и параллельного соединений нескольких фильтров первого или второго порядка.

14.4. Приемы построения цифровых фильтров по заданным характеристикам

Как отмечалось, задача построения нерекурсивного фильтра по заданной импульсной характеристике решается просто. Однако чаще бывает задана его частотная (или операторная) характеристика. По­скольку методы аппроксимации желательных характеристик частот­ных фильтров рациональными функциями передачи F (р) с максималь­но плоскими и равноволновыми характеристиками хорошо разработаны (см. § 6.14), то будем считать, что требуемая характеристика задана функцией F (р) вида

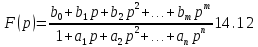
Она является характеристикой аналогового фильтра-прототипа. Задача заключается в переходе от функции F (р) к функции F (z). По F (z), как было показано, строится одна из канонических схем, чем и определяется алгоритм работы цифрового фильтра.

Сложность перехода от F (р) к F (z), несмотря на сходство формул (14.10) и (14.12), заключается в однозначном соответствии функции F (р) дифференциальному уравнению, а функции F (z) разностному урав­нению. При переходе от дифференциального уравнения к разностному меняются значения коэффициентов, как это было видно из рассмотрен­ного в § 2.14 простого примера.

Коэффициент а в дифференциальном уравнении преобразовался 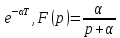в -в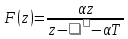В ряде простых случае можно пользоваться таблицей соответствий междуL- и z-преобразованиями (см. табл. 1.2).

Иногда функцию F (р) можно разложить на простые дроби вида а/(р + а) и воспользоваться известными соответствиями, но в боль­шинстве практически важных случаев приходится искать другие прие­мы преобразования F (р) в F (г).

На практике применяют так называемое билинейное z-преобразование, при котором используют подстановку

Это преобразование было найдено формально математически при поисках способа преобразования комплексной плоскости р в плоскость z. Пояснить его можно так. Заметим, что частотные характеристики дискретных фильтров, как и спектры дискретных сигналов, периодич­ны. Проиллюстрируем это на примере простого нерекурсивного фильт­ра (рис. 14.7, а). Для него

Имея в виду, чтои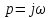, получим:

Выражение (14.14) содержит два слагаемых: вектор направленный вдоль вещественной оси, и вращающийся вектор .Модуль функцииF(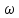) будет периодически изменяться от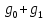до (рис 14.7,б).

Таким образом, задачу перехода от функции F (р) к функции F (г) можно сформулировать как задачу перехода от непериодической частотной характеристики к периодической. Характеристика должна повторяться далеко вне рабочего диапазона частот, ^то легко дости­гается выбором периода дискретизации соответственно малым (см. рис. 14.7, б). И поскольку повторение характеристики происходит вне рабочего диапазона, как она повторяется—безразлично.

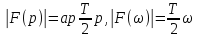Рассмотрим теперь функцииПусть рабочий диапазон кончается в точке.Введем теперь периодичность, заменивна(рис. 14.14). В рабочем диа­пазоне частот, т. е. при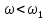

Равенству (14.15) соответствует соотношение

и, следовательно,

Из рис. 14.8 видно, что вблизи со_х происходит расхождение между x и tgx. Его можно уменьшить введением преобразования масштаба частот:

где 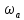— частота среза аналогового фильтра-прототипа;

—частота цифрового фильтра, на которой характеристики фильтров должны совпадать.

Как видно, при tgx = х выражение (14.17) дает =. В соот­ветствии с выражением (14.17) следует пересчитывать частоты среза и частоты, на которых должно гарантироваться определенное ослабление.С учетом сказанного, а также, имея в виду, что F (г) должны быть пред­ставлены в виде функции от, дробно-рациональное преобразование (14.15) для ФНЧ имеет вид:

Пусть, например, требуется рассчитать цифровой фильтр нижних частот с максимально плоской характеристикой в по­лосе пропускания и затуханием 3 дБ на частоте среза f_с = 1 кГц, ослаблением не менее 20 дБ на частоте f₂ = 2 кГц и частотой дискретизации f_д = 10 кГц. Сна­чала определим характерные ча­стоты фильтра-прототипа. Часто­те среза цифрового фильтра соответствует частота срезафильтра-прототипа:

где— интервал дискретизации.

Подставляя числовые данные, получим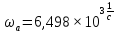. Аналогично частотецифрового фильтра соответствует частота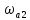фильтра-прототипа:

Таким образом, фильтр-прототип должен иметь затухание 3 дБ на ча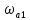стоте =затухание не менее 20 дБ на частоте

Определим теперь частотную характеристику фильтра-прототипа. Вспомним, что максимально плоскую характеристику имеют фильтры Баттерворта, описываемые выражением

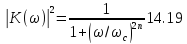
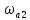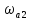Найдем порядок фильтра-прототипа, удовлетворяющего указан­ным требованиям. Отношение частот c/= 2,236. Задаваясь на частотеослаблением не менее 20 дБ (т. е. в 10 раз), из выражения (14.19) определим порядок фильтра: (1 + 2,236ⁿ) 100, откудаn2,85. Принимаем n = 3. Фильтр Баттерворта третьего порядка на частоте обеспечивает ослабление сигнала, равное 10lg [1 ++ (2,236)⁶] ≈21 дБ, что превышает заданные требования к фильтру. Найдем теперь передаточную функцию фильтра-прототипа — фильтра Баттерворта третьего порядка. Согласно табл. 6.3 можно написать:

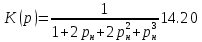
Откуда

Системная функция (14.21) может быть реализована в виде цепочеч­ного соединения двух фильтров первого и второго порядка, для чего эту функцию представим в виде произведения двух системных функций:

Схема цифрового фильтра, соответствующая системной функции (14.22), приведена на рис. 14.9.