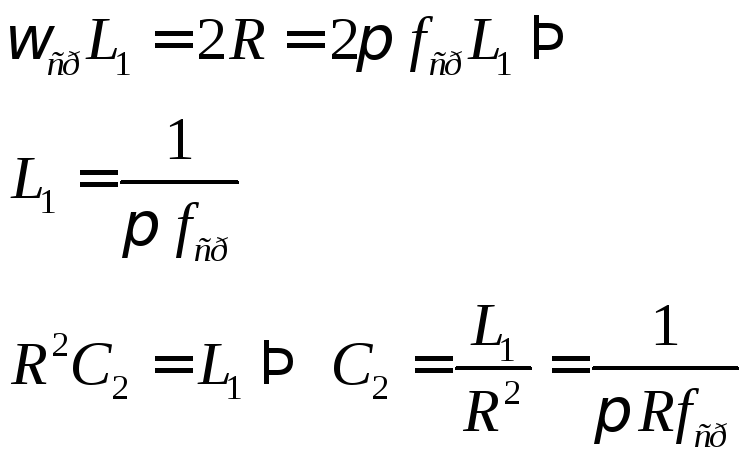6. Цепочные фильтры типа k.

Такие у которых в ветвях стоят обратные двухполюсники.

(*)z₁ ^. z₂ =R²=const

R-номинальное характеристическое сопротивление.

(6.1) - ФНЧ

м

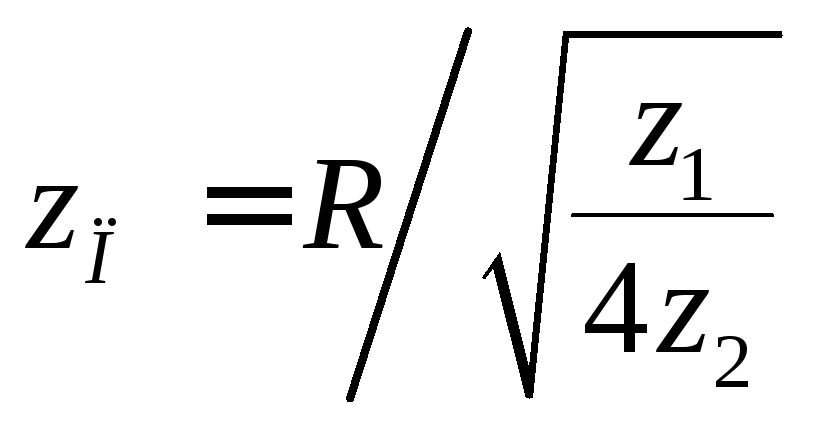
6.1 Фильтр нижних частот типа k.

6.1.1. схема фильтра:

Поскольку ФНЧ должны пропускать постоянный ток и срезать верхние частоты, то в продольной ветви целесообразно поставить индуктивность, а в продольной – емкость.

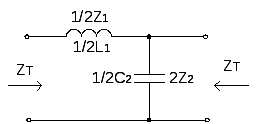
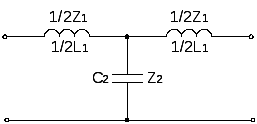
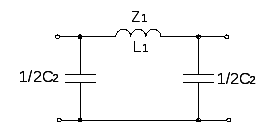
Г-обратное звено Звено «Т» Звено «П»

6.1.2. Графическое и аналитическое определение частоты среза.

Для определения частоты среза используем (5.11).

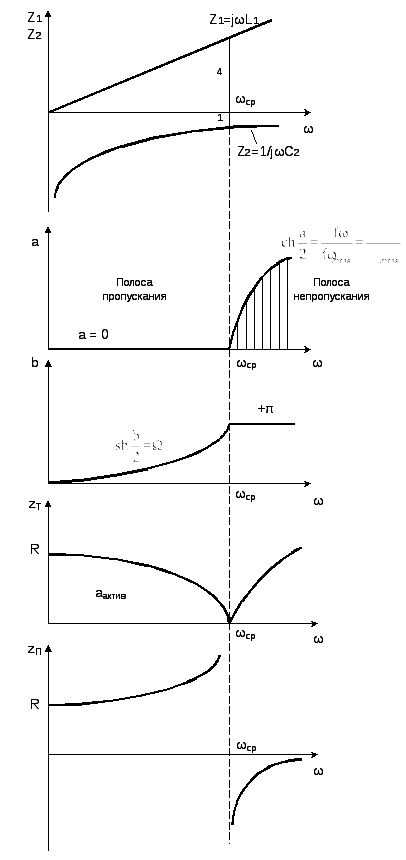
6.1.5. Расчет элементов фильтра нижних частот (ФНЧ)

Воспользуемся (5.8) приf=f_ср

Назовем R-номинальным характеристическим сопротивлением фильтра.

Условие (5.8) можно записать по-другому – умножим обе части на Z₁, тогда получим: , тогда получаем новое условие:

(6.3) X₁=-2R при f=f_ср

Умножим обе части (5.11) на Z₂, тогда получим:

(6.4) X₂=+R/2 при f=f_ср

Используя формулы (6.3) и (6.4) определим графически f_ср

Частоту среза определим графически из условия (5.11).

Но есть условия (6.3) и (6.4) по этим условиям для определения частоты среза достаточно иметь один график. Откладываем по (6.3) на оси Z₁Z₂ величину 2R, проводим прямую параллельную оси частот до пересечения с графиком Z₁ и из точки пересечения опускаем перпендикуляр, так нашли частоту среза, если задан график Z₁. Если задан график Z₂ то откладываем на оси сопротивления величину R/2. Дальнейшие рассуждения аналогичны.

Аналитически частоты среза:

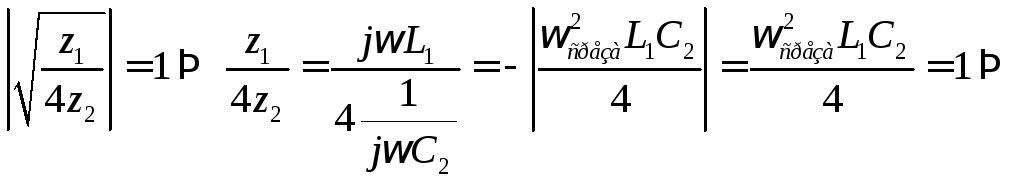
(6.5)

6.1.3. Расчет a и b, затухания фазовых коэффициентов по соотношениям (5.7) и (5.8).

(6.6)

- относительная или нормированная частота (нормирование выполнено по f_ср).

Для полосы пропускания будем иметь:

(6.7)

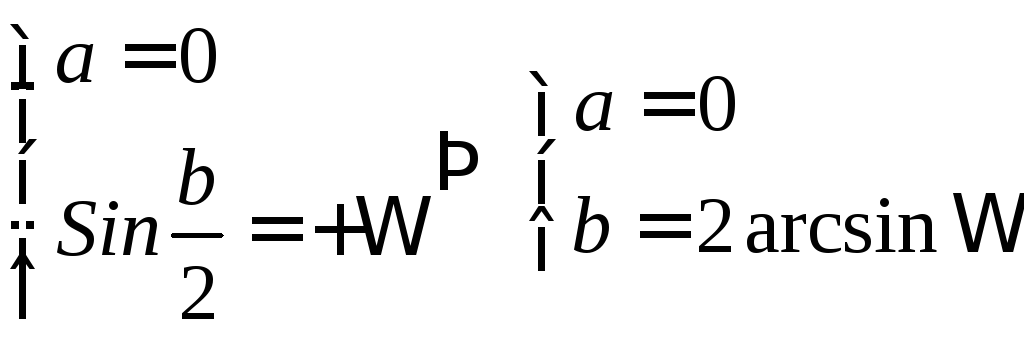
В фазовом коэффициенте выбираем знак плюс потому, что в продольной ветви индуктивность, ток нагрузки отстаем от входного напряжения.

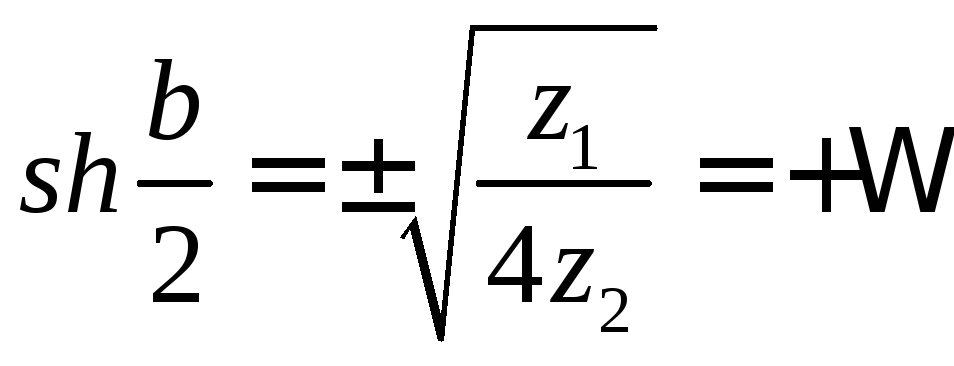
В продольной ветви индуктивности, поэтому ток в нагрузке отстает от напряжения на входе.

Для f>f_ср:

(6.8)

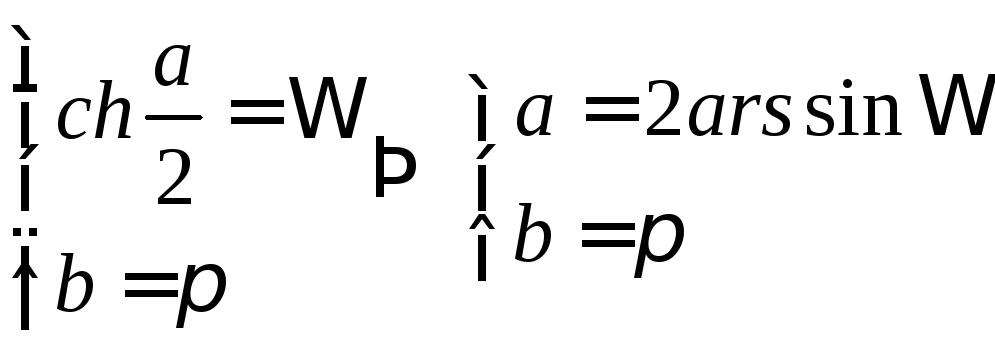
6.1.4. Расчет z_Т и z_П:

(6.9)

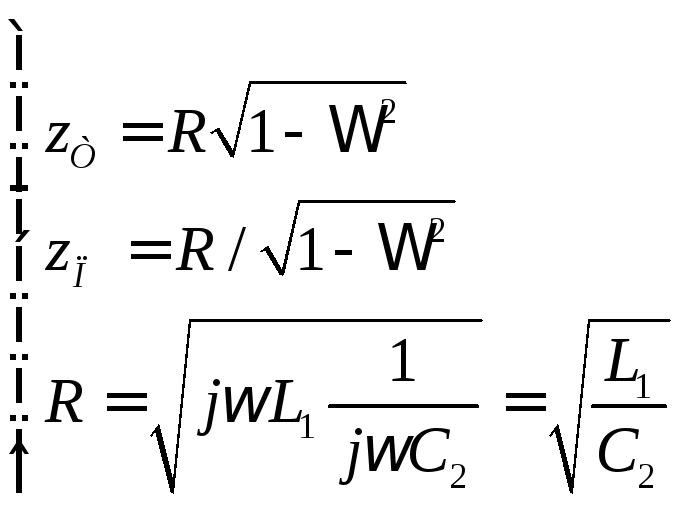
-параметрическая частота, нормировка произведена по частоте среза.

Из (6.9) до частоты среза в полосе пропускания сопротивления активного характера, т.к.. В полосе непропускания т.е. присопротивление реактивное, т.к. под корнем отрицательное число.

Т.к. при , азакоротиться, значит на входе индуктивность.

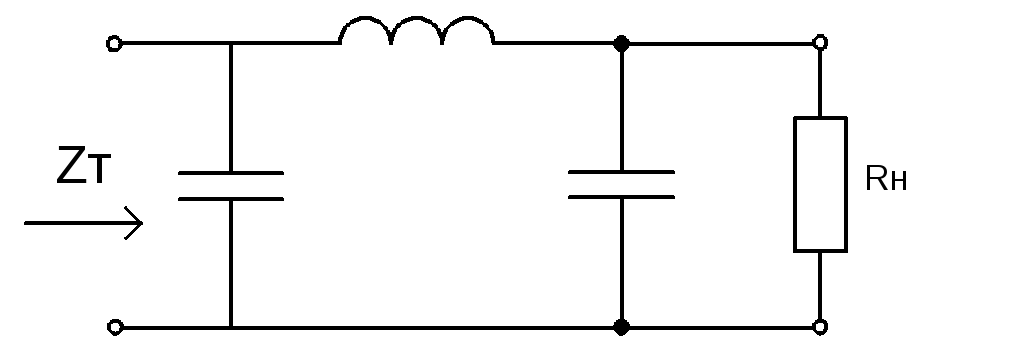
Возьмем данную схему и воспользовавшись ей построим Zп.

На постоянном токе продольная ветвь представляет из себя R=0, сопротивление емкости в поперечной ветви . Схема тяготеет к резонансу токов, а при резонансе токов, поэтому доf_ср график имеет такой вид.

При -емкостной характер.

В полосе пропускания Zт и Zп активно, это означает что фильтр способен отобрать энергию от источников (активное сопротивление мы всегда рассматриваем как потребитель энергии) но сам фильтр состоит из реактивных элементов, значит он не потребляет отобранную энергию, а передает в нагрузку.

В полосе непропускания Zп реактивно это значит, что фильтр не отбирает энергию от источника и не передает в нагрузку.

(6.10)

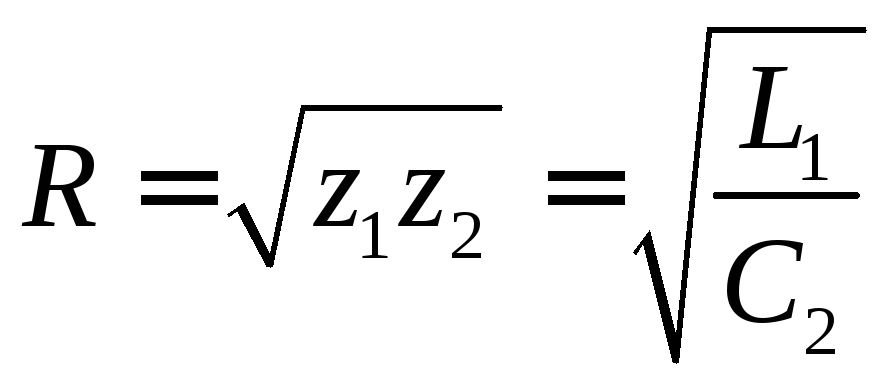
Замечание: мы говорим об идеальном фильтре, выполненном из идеальных элементах (без потерь).

Задача: Дано fср и Rн, требуется определить элементы фильтра L1 и C2.

Принимаем что R=Rн

(1) X₁=2R

(2)

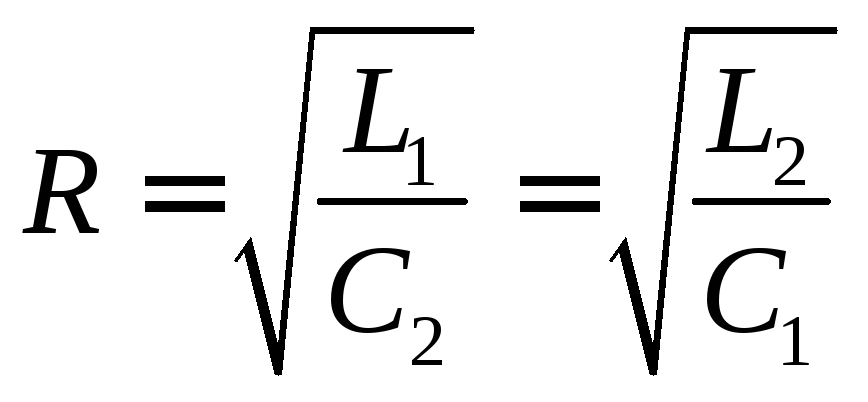
(3)

Имеем: