Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Башкирский Государственный Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Экзамен пр Матану.docx

Скачиваний:

436

Добавлен:

18.03.2016

Размер:

1.69 Mб

Скачать

☆

1 / 91 2 3 4 5 6 7 8 9 > Следующая >>>

№3:» Бесконечно малые функции и их свойства».

Определение: Функция называется бесконечно малой функцией (б.м.ф.) при х→а (или в точке х=а ), если

Пример: у=х является б.м ф, при х→0.

Основные свойства бесконечно малых функций

1° Сумма конечного числа б.м функций является функцией б.м.

2° Произведение б.м функции на ограниченную есть функция б.м.

3° Произведение двух б.м функций есть функция б.м.

4° Произведение б.м функции на константу является б.м функцией.

5° Частное от деления б.м функции на функцию, предел которой не равен нулю, есть функция б.м.

6° Функция 1/а(х) , обратная к б.м функции а(х) ≠0 , есть функция бесконечно большая. Верно и обратное.

№7:»Первый и Второй замечательный предел»

Замеча́тельные преде́лы — термин, использующийся в советских и российских учебниках по математическому анализу для обозначения некоторых широко известных математических тождеств со взятием предела. Особенно известны:

Первый замечательный предел:

Определение: Первым замечательным пределом называется предел отношения синуса бесконечно малой дуги к той же дуге, выраженной в радианной мере:

Приведённое выше равенство основано на эквивалентности бесконечно малых. Следовательно, верно равенство и следующего отношения:

Доказательство:

Рассмотрим односторонние пределы ии докажем, что они равны 1.

Пусть . Отложим этот угол на единичной окружности (R = 1).

Точка K — точка пересечения луча с окружностью, а точка L — с касательной к единичной окружности в точке(1;0). Точка H — проекция точки K на ось OX.

Очевидно, что:

(1)

(где S_sectOKA — площадь сектора OKA)

(из : |LA | = tgx)

Подставляя в (1), получим:

Так как при :

Умножаем на sinx:

Перейдём к пределу:

Найдём левый односторонний предел:

Правый и левый односторонний пределы существуют и равны 1, а значит и сам предел равен 1.

Следствия:

Вторым замечательным пределом называется равенство

, где

е-иррациональное число.

В случае второго замечательного предела имеем дело с неопределенностью вида единица в степени бесконечность .

Доказательство для натуральных значений .

Зная, что второй замечательный предел верен для натуральных значений x, докажем второй замечательный предел для вещественных x, то есть докажем, что . Рассмотрим два случая:

1. Пусть . Каждое значение x заключено между двумя положительными целыми числами:, где— это целая часть x.

Отсюда следует: , поэтому

Если , то. Поэтому, согласно пределу, имеем:

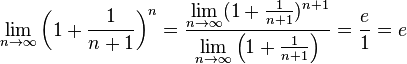
По признаку (о пределе промежуточной функции) существования пределов .

2. Пусть . Сделаем подстановку, тогда

Из двух этих случаев вытекает, что для вещественного x.

Следствия

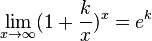
для ,

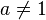
№5:»Непрерывность функции, точки разрыва, их классификация».

Непрерывная функция — функция без «скачков», то есть такая, у которой малые изменения аргументаприводят к малым изменениям значения функции.

Функция называетсянепрерывной в точке , если:

функция определена в точкеи ее окрестности;
существует конечный предел функциив точке;
это предел равен значению функции в точке , т.е.

Замечание:

При нахождении предела функции , которая является непрерывной, можно переходить к пределу под знаком функции, то есть

Пример

Задание. Вычислить предел

Решение.

Ответ.

Точки разрыва функции и их классификация:

Определение точки разрыва

Определение

Точка , в которой нарушено хотя бы одно из трех условийнепрерывности функции, а именно:

функция определена в точке и ее окрестности;
существует конечный предел функциив точке;
это предел равен значению функции в точке , т.е.

называется точкой разрыва функции.

Пример

Функция не определена в точке, а значит, эта точка является точкой разрыва указанной функции.

Точка разрыва первого рода

Определение

Если в точке существуют конечные пределыи, такие, что, то точканазываетсяточкой разрыва первого рода.

Пример

Функция в точкеимеет разрыв первого рода, так как

, а

Точка разрыва второго рода

Определение

Если хотя б один из пределов илине существует или равен бесконечности, то точканазываетсяточкой разрыва второго рода.

Пример

Для функции точка- точка разрыва второго рода, так как.

Точка устранимого разрыва

Определение

Если существуют левый и правый пределы функциив точке и они равны друг другу, но не совпадают со значением функциив точке:или функцияне определена в точке, то точканазываетсяточкой устранимого разрыва.

Пример

Рассмотрим функцию . Найдемодносторонние пределыи значение функции в точке:

Так как и не равны значению функции в точке, то точка- точка устранимого разрыва.

№6: «Предел последовательности».

Определение: число называется пределом последовательности, если для любой его окрестности (заранее выбранной) существует натуральный номер – ТАКОЙ, что ВСЕ члены последовательности с бОльшими номерам окажутся внутри окрестности.

Число называется пределом последовательности, если , , : . Предел последовательности обозначается. Куда именно стремится, можно не указывать, поскольку, оно может стремиться только к.

Свойства:

Если предел последовательности существует, то он единственный.
(если оба предела существуют)
(если оба предела существуют)
(если оба предела существуют и знаменатель правой части не ноль)
Если и, то(теорема «о зажатой последовательности», также известная, как «теорема о двух милиционерах»)

№1.

8) Некоторые важные пределы

Если угол а выражен в радианах, то

При нахождении многих пределов применяются следующие пределы:

(13.19)

(13.20)

(13.21)

Частными случаями формул (13.19) и (13.20) являются соответственно формулы:

(13.22)

(13.23)

При нахождении пределов видаНеобходимо иметь

В виду следующее:

1) если существуют конечные пределы

2) еслиИ, тоНаходится с помощью формул

3) еслиТо, положивГде

ПриПолучим

Пример 13.12. Найти

ПриВыражениеПолучаем неопределенность

ВидаЧтобы раскрыть ее, введем новую переменную по формулеОткудаКогдаПереходя к пределу

С использованием формул (13.13) и (13.18), находим

В частности, приПолучаем

Пример 13.13. Найти

Разделив числитель и знаменатель наИ воспользовавшись результатом примера 13.12, получим

Пример 13.14. НайтиПреобразуя эту дробь и применяя первую из формул (13.17), находим

Пример 13.15. Найти

Преобразуя данную функцию, вводя новую переменнуюИ применяя

Формулу (13.21), находим

9) Производная. Геометрический и физический смысл производной

Перейти к списку задач и тестов по теме "Производная. Геометрический и физический смысл производной"

Определение: Производной функции f(x) (f'(x₀)) в точке x₀ называется число, к которому стремится разностное отношение , стремящемся к нулю.

Производные элементарных функций.

Правила дифференцирования.

Если у функций f(x) и g(x) существуют производные, то

Производная сложной функции:

Геометрический смысл производной. Производная в точке x₀ равна угловому коэффициенту касательной к графику функции y=f(x) в этой точке

Уравнение касательной к графику функции y=f(x) в точке x₀ :

Физический смысл производной.

Если точка движется вдоль оси х и ее координата изменяется по закону x(t), то мгновенная скорость точки:

10) Производные некоторых основных элементарных функций

В этом пункте мы найдем производные следующих основных элементарных функций: постоянной (константы) степенной функции с натуральным показателем , показательной функции логарифмической функции и тригонометрических функций .

Производные остальных основных элементарных функций будут найдены в последующих пунктах. 1. Производная постоянной Так как функция сохраняет постоянное значение на всей числовой оси, то в произвольно выбранной точке любому приращению аргумента соответствует приращение функции , равное нулю. Поэтому

Итак,

2. Производная степенной функции с натуральным показателем . Пусть х — произвольно выбранная точка, -приращение аргумента в этой точке и — соответствующее приращение данной функции. Тогда по формуле бинома Ньютона

или

Следовательно,

Таким образом,

3. Производная показательной функции Давая приращение произвольно выбранному значению аргумента получим следующее приращение показательной функции:

Следовательно,

так как (см. гл. V, § 2, п. 2, пример 3).

Таким образом,

В частности, при получим

так как

4. Производная логарифмической функции Возьмем любое значение из области определениялогарифмической функции и дадим ему приращение Тогда приращение функции

Поэтому

Для того чтобы найти этот предел, сделаем следующее преобразование:

Принимая во внимание, что величина постоянна и что при также и по формуле (25) гл. V, § 2 получим

Итак,

(19)

или

так как

В частности, при получим

так как

5. Производные функций Пусть — приращение произвольно выбранного значения аргумента функции Тогда приращение этой функции

Следовательно,

так как по формуле (18) гл. V, § 1, п. 7

Таким образом,

Аналогично выводится формула для производной функции

11) Основные правила дифференцирования

Установим правила, по которым можно было бы находить производные суммы, произведения и частного функций, зная производные слагаемых, сомножителей, делимого и делителя.

Эти правила мы сформулируем в следующих теоремах.

Теорема I. Если функции дифференцируемы в данной точке , то в той же точке дифференцируема и их сумма, причем производная суммы равна сумме производных слагаемых:

Доказательство. Рассмотрим функцию . Приращению аргумента соответствуют приращения

функций и и и. Тогда функция у получит приращение

Следовательно,

Так как по предложению функции и и v дифференцируемы, то

и, следовательно, .

Итак,

Замечание. Формула (23) легко обобщается на случай любого конечного числа слагаемых:

Пример 1. Найти производную функции Решение. Применяя вначале формулу (24), а затем формулы (16), (21) и (20), получим

Теорема 2. Если функции и дифференцируемы в данной точке , то в той же точке дифференцируемо и их произведение. При этом производная произведения находится по следующей формуле: