Добавил:

TooL Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Тульский Государственный Университет

Предмет:

Физика

Файл:

Ю.Н. Колмаков, Ю.А. Пекар, Л.С. И.М. Лагун, Л.С. Лежнева. Механика и теория относительности. Лекции. / mech-lec-TulGU

.pdf

Скачиваний:

138

Добавлен:

22.01.2014

Размер:

3.9 Mб

Скачать

☆

<<< < Предыдущая 1 2 34 / 184 5 6 7 8 9 10 11 12 13 14 15 16 17 18 > Следующая >>>

6. Неинерциальные системы отсчета. Силы инерции

	ω2 R з			2			1		2
g = g0 1 −			cos		ϕ	= g0 1 −		cos		ϕ .	(2.14)
g = g0 1 −			cos		ϕ	= g0 1 −		cos		ϕ .	(2.14)
		g0					290
		g0					290
(Заметим, что из-за сплюснутости Земли коэффициент в формуле
(2.14) не 1/ 290 ,	а	1/190 .)
При движении по Земле со скоростью vG' = 5 км / час на пешехода с
массой m = 60 кг		действует очень малая кориолисова сила.									Ее макси-
мальная величина		F кор = 2mω2vG' ≈ 0, 012 Н.							Но в летящем со скоро-
стью v ' =1000 км/ час			самолете эта сила, толкающая человека вбок, мо-
						жет возрасти до ощутимой величи-
						ны 2, 4 Н.
							Во время первой мировой вой-
						ны в сражении британского и
						немецкого флотов у Фолклендских
						островов все точно пристрелянные
						пушки английских кораблей стали
						посылать			снаряды на		расстояние
						100 м от цели. Причина была в том,
						что военные моряки не учли про-
						стые законы физики. Прицелы бы-
Рис.2.14						ли выверены у берегов Англии, в
Рис.2.14						северном полушарии, а Фолкленды
						находятся в южном полушарии. Из

формулы (2.11) и рис.2.14 видно, что сила Кориолиса в разных полушариях отклоняет летящие снаряды в разные стороны.

		Из того же рисунка видно, что пассаты
		(ветры, дующие от тропиков к экватору) в
		обоих полушариях будут отклоняться к запа-
		ду, а текущие реки будут отклоняться в се-
		верном полушарии к правому берегу, а в юж-
		ном – к левому.
		Рассмотрим еще один пример – враще-
		ние жидкости в сосуде (рис. 2.15). Уравнение
		движения (2.8) можно записать для любой
		"частицы" жидкости – бесконечно малого
		кубика с поперечным сечением ∆S , который
	Рис.2.15	вместе с жидкостью вращается с угловой
	Рис.2.15	скоростью ω. Центростремительное ускоре-
		скоростью ω. Центростремительное ускоре-

32 Глава 2. Динамика. Законы Ньютона и их следствия

ние этого кубика создается, главным образом, силами гидростатического давления: ∆mω2r = p '∆S − p∆S =ρg (h'−h)∆S . Отсюда следует, что

h' > h , и поверхность вращающейся жидкости должна принимать форму воронки (рис.2.15). По той же причине поверхность реки в месте поворота будет наклонена в сторону поворота.

Учтем теперь силы вязкого трения. Из-за них жидкость практически не движется вблизи дна сосуда, т.е. с высотой скорость вращения увеличивается. Если перейти в неинерциальную систему отсчета, вращающую-

ся со средней скоростью жидкости ωG , то в этой системе верхние слои

жидкости будут двигаться со скоростью vG' , опережая вращение системы, а нижние слои будут отставать. Кориолисовы силы приведут к появлению поперечных циркулярных потоков (правая часть рис.2.15). Такие потоки собирают чаинки в аккуратную кучку в центре стакана. Эти же потоки будут размывать один из берегов реки в месте ее изгиба и наносить ил на другой, пологий берег.

1. Работа силы

Рис.3.1

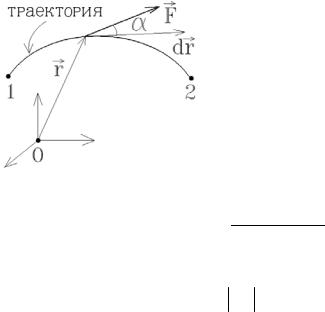
Глава 3.

Работа и энергия

Обычно приходится иметь дело с силой, переменной как по величине, так и по направ-

лению, и действующей на частицу, движущуюся по криволинейнойG траектории. На-

правление силы F составляет с траекторией угол α (вообще говоря, переменныйG ). За вре-

мя dt частица переместится на dr (рис.3.1), и

сила совершит над ней элементарную работу, которая по определению равна скалярному произведению вектора силы на вектор беско-

нечно малого перемещения:	G	G
			(3.1)
	dA = F dr.

Формулу (3.1) можно записать и по-другому:

dA = F drG cos α = F dl cos α = Fl dl,

где Fl - проекция силы на направление траектории, dl – элементарный

путь (рис.1.4). Выражение для работы при конечном перемещении из точки 1 в точку 2 будет выражаться интегралом:

2	G	G	(3.2)
A12= ∫F dr.			(3.2)
1

Если же на тело одновременно действуют несколько сил, то их суммарная работа равна алгебраической сумме работ каждой силы, или, ина-

че, равна работе результирующей силы			G	G
	G	G
	A рез = ∫Fрез dr		= ∫∑Fi	dr = ∑A i.
			i	i
Знак работы каждой силы в этой сумме зависит от направления век-
G	drGi . Сила совершает положительную работу, когда она на-
торов Fi и

правлена "по движению" (α< π2), и отрицательную – когда она направлена "против движения" ( α > π2 ).

34 Глава 3. Работа и энергия

Сила, перпендикулярная к траектории частицы, работы не совершает. Так, в частности, всегда равна нулю работа силы, действующей на

движущуюся заряженную частицуG со стороны магнитногоG поля:

Aмагн = ∫Fмагн drG = ∫q vG, B vGdt = 0.

Кроме того, надо учитывать, что drG – это перемещение точки при-

ложения силы. Например, при движении тела с закрепленным центром тяжести работа силы тяжести равна нулю! Помимо работы можно определить мощность силы, которая равна работе, совершенной за единицу времени:

	dA	G	G
P =		= F	v.	(3.3)
	dt

2. Кинетическая энергия частицы

Пусть на движущуюся частицу действует некоторая силаG FG . B результате движение частицы изменяется (меняется скорость v ). Найдем,

чему равна работа силы по изменению скорости частицы. Для этого запи-

шем второй закон Ньютона

dvG

= ∑FG

и умножим каждую его часть

скалярно на элементарное перемещение drG. В итоге получим:

dvG

G drG

G G

= mdv

= mvdv = ∑Fdr = d A.

G G

vx2

+v2y +vz2

Но vdv =v

= d

и поэтому

mv2

= dA .

Величину

K =

mv2

называют кинетической энергией частицы. Та-

ким образом, работа всех сил, действующих на частицу, идет на изменение ее кинетической энергии, т.е.

	mv2		mv2	2	G G
dK = dA или K2 − K1 =	2	−	1	= ∫	∑Fdr.	(3.4)
dK = dA или K2 − K1 =	2	−	2	= ∫	∑Fdr.	(3.4)
	2		2	1

3. Консервативные силы и потенциальная энергия			35
	3. Консервативные силы и потенциальная энергия
		Определение: сила, работа которой
		не зависит от формы и длины пути (от тра-
		ектории точки приложения силы), называ-
		ется консервативной силой (рис.3.2,а).
		Математически условие консерватив-
		ности силы выражается в виде:
		G G	(3.5)
		v∫Fdr = 0 .	(3.5)
		Действительно, как следует из рис.
	Рис.3.2	3.2,б и формулы (3.2), работа консерватив-
	Рис.3.2	ной силы на замкнутом пути в силу опре-
		ной силы на замкнутом пути в силу опре-
деления будет: Aзамкн = A12+ A 21 = A12 − A12 = 0 . Величина			G G
			v∫adr на-

зывается циркуляцией вектора aG . Поэтому условие (3.5) читается так :

циркуляция консервативной силы по любому замкнутому контуру равна нулю.

Из определения консервативной силы вытекает и еще одно важнейшее свойство: работу консервативной силы можноG представить, как изменение (убыль) некоторой скалярной функции U (r ) , зависящей только от

положения частицы (тела), которая называется потенциальной энергией: dA конс = FGконсdrG = −dU ,

или

2
U (rG1) −U (rG2 ) = −∆U = ∫FGконсdrG.	(3.6)
1

В том, что это действительно так, можно убедиться на примерах, рассмотренных в следующем параграфе.

Последняя из формул (3.6) являются определением потенциальной энергии. Из нее следует, что потенциальная энергия определена с точностью до произвольной постоянной. Так как определена только ее разность, то к выражению U можно добавить или вычесть

любую постоянную величину.

Например, потенциальную энергию тела (рис.3.3) можно вычислять относительно уровня любого этажа здания, относительно

Рис.3.3 уровня моря, относительно центра Земли и т.д.; величина ее при этом, конечно, будет

36		Глава 3. Работа и энергия

разной, но работа консервативной силы тяжести при перемещении тела m во всех случаях будет одной и той же!

Поэтому в каждом конкретном случае договариваются о начале отсчета потенциальной энергии (в какой именно точке следует считать

U= 0 из соображений удобства).

4.Потенциальная энергия центральных сил

						Определение: силы, действующие
					по прямой, соединяющей частицы, и за-
					висящие только от расстояния		r между
					ними, называются центральными. Об-
					щим для всех центральных сил будет
					следующий силовой закон:
		Рис.3.4				FGцентр(rG) = f (r) eGr ,	(3.7)
где eGr = rG r – единичный вектор, направленный от одной частицы к дру-
гой. Как видно из рис.3.4, при смещении одной из частиц на drG							получаем
eGr drG =	eGr		drG	cos α = dr ,	т.е. изменению расстояния между частицами.
eGr drG =	eGr		drG	cos α = dr ,	т.е. изменению расстояния между частицами.
Поэтому работа любой центральной силы будет:
					2	2
				A центр= ∫FGцентр drG = ∫ f (r) dr.
					1	1
Для любой функции					f (r)	результат интегрирования определяется
лишь начальным r1 и конечным						r2 положениями траектории, и может

быть записан в виде A центр=U (r1) −U (r2 ).

Поэтому любая центральная сила является консервативной, и частица в поле центральных сил обладает потенциальной энергией. Примерами центральных сил могут служить гравитационная, кулоновская и упругая силы.

Вычислим потенциальную энергию различных центральных сил. 1) Сила гравитационного притяжения:

FG	= −G	m1m2	eG	, поэтому	f (r) = −G	m1m2	. Выберем U = 0

грав		r2	r			r2

при r =∞ . ТогдаG работа перемещения частицы 2 (рис.3.5) из бесконечности в точку r будет:

5. Градиент потенциальной энергии		37

r		m m		m m
A = ∫	−G	1 2	dr =G	1 2	= 0 −U (r).
A = ∫	−G	r2	dr =G	r	= 0 −U (r).
∞		r2		r

					Следовательно, потенциальная энергия при-
					тяжения двух точечных масс
					Uграв(r) = −G			m1m2	.
					Uграв(r) = −G				.
	Рис.3.5							r
	Рис.3.5				2) Кулоновская сила:
FG					2) Кулоновская сила:
	(r) = k	q1q2	eG	, поэтому	f (r) = k	q1q2	. Если снова выбрать U = 0
	(r) = k		eG	, поэтому	f (r) = k		. Если снова выбрать U = 0
кул		r2	r			r2

при r =∞ , то для потенциальной энергии взаимодействия двух точечных зарядов получим выражение аналогичное предыдущему:

Uкул(r) = k q1q2

3) Сила упругости: FGупр = −k rG = −k r eGr ,rт.е. f (r) = −k r ( k – жесткость, r - удлинение деформируемого тела). Полагаем U = 0 при r = 0

	(рис.3.6), поэтому
	r	(−k r) dr = −		kr2			= −U (r).
	A = ∫	(−k r) dr = −			2		= −U (r).
	0				2
	0
	Итак, потенциальная энергия упругой
	силы (или упругой деформации)
Рис.3.6	Uупр(r) =		k r		2	.
			k r

		2

Отсюда, в частности, следует, что работа, которую надо совершить для удлинения пружины на r , равна k2r2 .

5. Градиент потенциальной энергии

Как следует		из определения	потенциальной			энергии	(3.6),
G	G	= −dU. . С учетом	G	G	G	G
dA конс = Fконс dr			dr	= idx + jdy + kdz получим:
−dU = Fxdx + Fydy + Fzdz . Отсюда, при перемещении вдоль оси							x , ко-

гда dy = dz = 0 , находим −dU = F dx , т.е. F		= −	dU		≡ −∂U .


x	x		dx	y,z=const	∂x

38		Глава 3. Работа и энергия

	Проекция консервативной силы на ось	x равна частной производ-

ной от потенциальной энергии по x - координате (частная производная берется по одной переменной в предположении, что все остальные пере-

менные не изменяются). Аналогично F = −

∂U

= −

∂U

∂y

∂z

Таким образом, консервативная сила выражается через потенциаль-

ную энергию следующим образом:

= −iG∂U − Gj ∂U

−kG∂U .

(3.8)

конс

∂x

∂y

∂z

Введем дифференциальный оператор “набла”:

∂

= i

+ k

(3.9)

∂x

∂y

∂z

Им можно подействовать

функцию f (x, y, z) .

на любую скалярную

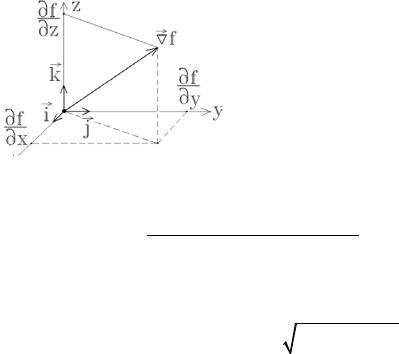
В результате получается вектор с про-

екциями

∂f

(рис.3.7), кото-

∂x

∂y

∂z

рый называется градиентом функции f :

(x, y, z) ≡ grad f (x, y, z)=

∂

(3.10)

Рис.3.7

+ j

+ k

f (x, y, z) .

∂x

∂y

∂z

Итак, зная потенциальную энергию частицы, можно простым диф-

ференцированием найти действующую на нее консервативную силу:

Наоборот, по

Fконс = − U

≡ −gradU.

(3.11)

выражению для силы можно интегрированием найти

потенциальную энергию частицы (формула (3.6)).

Пример: пусть U =

α , где r =

x2 + y2 + z2

и α = const . Тогда

G∂U

∂U

∂r

∂U

∂r

∂U ∂r

= − i

∂x

+ j

∂y

+ k

∂z

= −

∂r ∂x

+ j

∂r

∂y

+ k

∂r ∂z

∂U G

∂U rG

∂U

= −

+ j

+ k

= −

= −er

∂r

∂r r

∂r

5. Градиент потенциальной энергии		39

Таким образом, в случае действия центральных сил, зависящих только от r , при вычисленииG градиента можно использовать только радиаль-

ную часть оператора :

G	G ∂
r = −er			.
r = −er		∂r	.
		G	G	∂	α	G	α
Поэтому в рассмотренном примере F			= −er			= er		. При
Поэтому в рассмотренном примере F			= −er			= er	r2	. При
				∂r	r		r2

α = −G m1 m2 получается сила гравитации Ньютона, при α = k q1 q2 – сила Кулона.

Эквипотенциальные поверхности

Геометрическое место точек, в которых потенциальная энергия частицы (или потенциал) одинакова, называется эквипотенциальной поверх-

ностью. Уравнение такой поверхности имеет вид: U S = const .

При перемещении по этой поверхности dU = 0 , и из выражения FdrG G = Fl dl = −dU = 0 следует, что проекция силы Fl на эквипотенциальную поверхность всегда равна нулю. Поэтому

вектор консервативной силы всегда перпендикулярен эквипотенциальнойGповерхности.

Если n – единичный вектор нормали к эквипотенциальной поверх-

ности, то Fn = −∂∂Un , и при dU > 0 Fn < 0 , следовательно,

вектор консервативной силы направлен в сторону убывания (уменьшения) потенциальной энергии, и в этом же направлении под действием силы будут ускоряться все тела. Вектор grad U также на-

правлен по нормали к эквипотенциальной поверхности, но в сторону возрастания U , т.е. противоположно силе.

1) однородноеG поле тяжести: g = const

(рис.3.8); 2) гравитационное

поле точечной массы M :

FGграв = −G mrM2 eGr , изо-

Рис.3.8

Рис.3.9

браженное на рис.3.9. На

Рис.3.10

40		Глава 3. Работа и энергия

обоих рисунках штриховыми линиями изображены эквипотенциальные поверхности, а также показаны направления градиентов потенциальной энергии и сил тяготения.

6. Механическая энергия частицы и закон ее изменения

Сумма кинетической и потенциальной энергий частицы называется ее полной механической энергией: E = K +U .

Если на частицу действуют только консервативные силы, то с одной стороны, dA = −dU , а с другой стороны, как следствие второго зако-

на Ньютона, dA = dK . Поэтому −dU = dK или d (K +U )= dE = 0.

Иначе говоря, механическая энергия частицы, подверженной действию только консервативных сил, сохраняется. Отсюда, кстати, и на-

звание этих сил: “conservare” (лат.) – сохранять.

Неконсервативные силы

Неконсервативными называются силы, работа которых зависит от длины и формы пути. Отсюда следует, что на замкнутом пути работа неконсервативных сил не равна нулю, и с ними не связана потенциальная энергия.

Примерами неконсервативных сил являются: сила трения скольжения и силы вязкого трения. Так, из рис.3.10 видно, что работа силы трения скольжения зависит не от переме-

щения тела, а от длины пути: Aтр = −µN l , и не равна нулю при возвращении тела в исходную точку.

Пусть на частицу действуют как консервативные, так и неконсервативныеG силы. Тогда уравнение движения будет

m ddtv = ∑FGконс +∑FGнеконс . Умножая его скалярно на drG, получим:

m dvG drG = ∑FGконс drG +∑FGнеконс drG dK = −dU + dA неконс или dt


dE = d (K +U )= dAнеконс .	(3.12)

Изменение полной механической энергии частицы равно работе всех действующих на нее неконсервативных сил:

2 G G

∆E = A неконс = ∫F неконс dr.

<<< < Предыдущая 1 2 34 / 184 5 6 7 8 9 10 11 12 13 14 15 16 17 18 > Следующая >>>

Соседние файлы в папке Ю.Н. Колмаков, Ю.А. Пекар, Л.С. И.М. Лагун, Л.С. Лежнева. Механика и теория относительности. Лекции.

#
22.01.20143.9 Mб138mech-lec-TulGU.pdf
#
22.01.20143.32 Mб747mech-zad-TulGU.pdf