Добавил:

TooL Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Тульский Государственный Университет

Предмет:

Физика

Файл:

Ю.Н. Колмаков, Ю.А. Пекар, Л.С. И.М. Лагун, Л.С. Лежнева. Механика и теория относительности. Лекции. / mech-zad-TulGU

.pdf

Скачиваний:

744

Добавлен:

22.01.2014

Размер:

3.32 Mб

Скачать

☆

1 / 191 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 > Следующая >>>

Министерство образования Российской Федерации

Тульский государственный университет

Ю.Н.КОЛМАКОВ, Ю.А.ПЕКАР, В.А.СЕМИН

Механика

теория относительности

Задачи и методы их решения

Тула 2002

УДК 537(07)

Механика и теория относительности. Задачи и методы их решения: Учеб. пособие /Ю.Н.Колмаков, Ю.А.Пекар, В.А.Семин; Тул.гос.ун-т. Тула, 2002. 189 с.

ISBN 5 – 7679 – 0206 – 2

Подробно рассмотрены методы решения задач по различным темам раздела “Механика и основы специальной теории относительности” курса общей физики. Кроме того, приведены тексты свыше 450 задач различной степени сложности по этим темам.

Предназначено для проведения семинарских и практических занятий со студентами всех специальностей инженерно-физического и инженер- но-технического профилей. Пособие может быть использовано студентами в процессе самостоятельной подготовки к этим занятиям и при индивидуальной работе.

Ил.: 244. Библиогр.: 13.

Печатается по решению библиотечно-издательского совета Тульского государственного университета.

Рецензент: канд. физ.-мат. наук, проф. Ю.Ф.Головнев, Тул. гос. пед. ун-т им. Л.Н. Толстого.

	Оглавление
Предисловие ..................................................................................................		4
Глава 1. Кинематика....................................................................................		5
Глава 2. Динамика .....................................................................................		22
Глава 3.	Законы сохранения.....................................................................	51
Глава 4.	Гармонические колебания........................................................	71
Глава 5.	Специальная теория относительности (СТО).......................	90
Глава 6.	Задачи для индивидуальной работы.......................................	99
1. Кинематика.....................................................................................		99
	Тематика задач....................................................................	114
2. Динамика.......................................................................................		116
	Тематика задач....................................................................	137
3 Законы сохранения........................................................................		139
	Тематика задач....................................................................	160
4 Колебания ......................................................................................		162
	Тематика задач....................................................................	177
5 Релятивистская механика.............................................................		179
	Тематика задач....................................................................	186
Библиографический список......................................................................		187

ПРЕДИСЛОВИЕ

В соответствии с современными требованиями, предъявляемыми к высшей школе, возрастает роль практических и семинарских занятий, основная цель которых – научить студента не только решать стандартные задачи, но и самостоятельно оценивать возможности применения различных методов для решения специальных задач.

Целью данного пособия является подробное изложение и обсуждение приемов и способов решения задач по всем темам части курса общей физики “Механика”, включая задачи по кинематике, динамике, законам сохранения в механике, колебаниям механических систем и механике специальной теории относительности.

Пособие разбито на две части. Первая часть (главы 1 – 5) содержат объяснение способов решения основных типов задач. В них рассмотрены различные методы и специальные приемы использования законов физики

впроцессе решения. Знание этих методов позволяет решить любую из задач, предлагаемых для самостоятельной работы во второй части пособия (глава 6). Необходимый для работы теоретический материал можно найти

вразличных учебниках, например, [1] – [4].

При подборе текстов задач для самостоятельного решения были использованы различные пособия, например, [5] – [13] и другие, причем главными критериями выбора было соответствие содержания задачи иллюстрируемому ею физическому закону и связь условий задачи с возможным практическим применением изучаемых закономерностей. Для удобства использования все тексты задач сгруппированы по различным темам курса; к ним прилагается список тематического содержания, в котором указаны основные законы, используемые при решении задачи, а также обозначена степень ее трудности, отражающая, в первую очередь, объем и уровень сложности применяемого при решении математического аппарата, а также нестандартность подхода при использовании исходных физических законов.

Как правило, решение всех предлагаемых задач предусматривает применение методов высшей математики в объеме стандартного вузовского курса.

Глава 1

Кинематика

Кинематика прямолинейного движения

	Задача 1.1
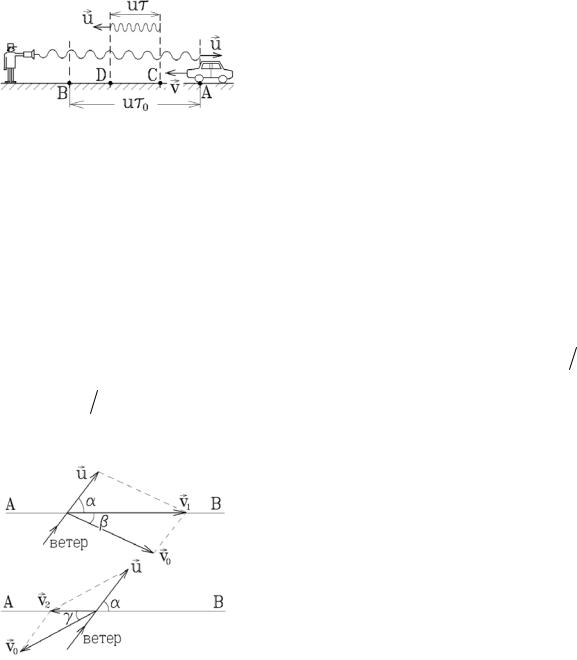
	Ультразвуковой радар (сонар) испускает
	импульсы с длительностью τ0 = 6 мкс. Чему
	равна скорость v движущегося навстречу ав-
	томобиля (рис.1.1), если отраженные от него
	импульсы имеют длительность	τ = 5 мкс ?
рис. 1.1	Скорость звука в воздухе u = 330	м/с .
	Решение

Пусть автомобиль встречает передний фронт звукового импульса в точке A . В это время задний фронт приближающегося со скоростью u им-

пульса находится в точке B на расстоянии BA = uτ0 (рис.1.1)

Задний фронт импульса автомобиль встретит спустя время t1 в точке

C , где BC = u t1 , CA = vt1 , то есть (u +v)t1 = uτ0 и t1 = uτ0 (u +v). К

этому моменту передний фронт отраженного импульса успел пролететь

расстояние	DA = u t1 . Поэтому длина отраженного импульса
DC = DA −CA = u t1 −vt1 = u τ , а его длительность			τ = (u −v)t1 u =
= (u −v)τ0	(u +v).Отсюда скорость автомобиля v =	τ0	−τ	u =108 км/ч .
		τ0
			+τ

Задача 1.2

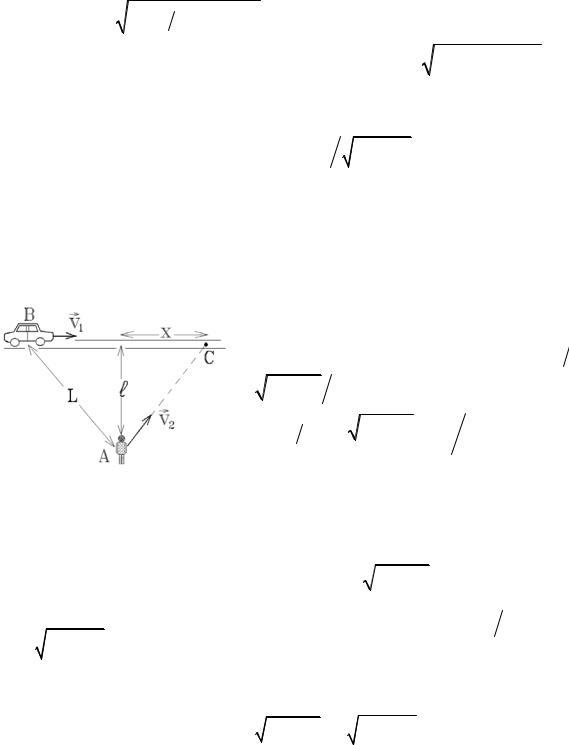
Какой будет продолжительность перелета из А в В и обратно, если в течение всего полета под углом α к трассе дует ветер со скоростью u ? Скорость аппарата относительно воздуха равна v0 , а длина трассы между А и

В равна l . При каком направлении ветра продолжительность полета максимальна?

Решение

На основании теоремы сложения скоростей рис.1.2 имеем: vG1,2 = vG+uG , где vG1,2 - скорости аппарата относительно земли при движении из А в В и обратно, направленные

вдоль линии, соединяющей А и В (рис.1.2). Теорема синусов дает

Глава 1. Кинематика

u sin α = v0 sin β

и u sin α = v0 sin γ , откуда

следует,

что β = γ . Поэтому

cosβ = cos γ =

−(u v )2 sin2

α . Продолжительность полета

t =

vo2 −u2 sin2 α

(1.1)

v0 cosβ+u cos α

v0 cos γ −u cos α

v2 −u2

Как следует из формулы (1.1), максимальное время полета получится при

sin α = 0 , т.е. при α = 0 :	t	max	= 2lv	v2	−u2 .
		max	0	0

Задача 1.3

Машина движется по прямому участку шоссе с постоянной скоростью v1 = 60 км/час. Пешеход, находившийся первоначально на расстоянии

l = 90 м от шоссе, бежит со скоростью v2 =18 км/час. При каком наименьшем начальном расстоянии L до машины пешеход успеет встретиться с ней?

				Решение
	Точка встречи C показана на рис.1.3. Пе-
шеход добежит до нее за время t2 = AC v2 =
=	l2 + x2	v2 ,	а	машина			доедет за	время
t	= BC v		2	−l	2		v . Если	t ≥ t		,
t	= BC v	=	L	−l		+ x	v . Если	t ≥ t	2	,
1	1						1	1	2

рис. 1.3

то пешеход успеет встретиться с машиной.

Он должен бежать к такой точке C шоссе,

чтобы максимально опередить машину, т.е. t1 −t2 = max .

Из условия экстремума

d (t1 −t2 )

−

= 0 получаем

l2 + x2

x =

v2l

(можно проверить, что в этой точке d 2 (t −t

) dx2 < 0 , т.е.

2 −v

выполнено условие максимума). Подставляя найденное оптимальное расстояние x , находим:

(t −t	2	)	max	=	L2 −l2	−	l	v12 −v22	.	(1.2)

1					v1			v1v2

Чем меньше начальное расстояние L до машины, тем меньше время опережения. При (t1 −t2 )max = 0 и машина, и пешеход достигнут точки

встречи одновременно. Из уравнения (1.2) при этом условии получим

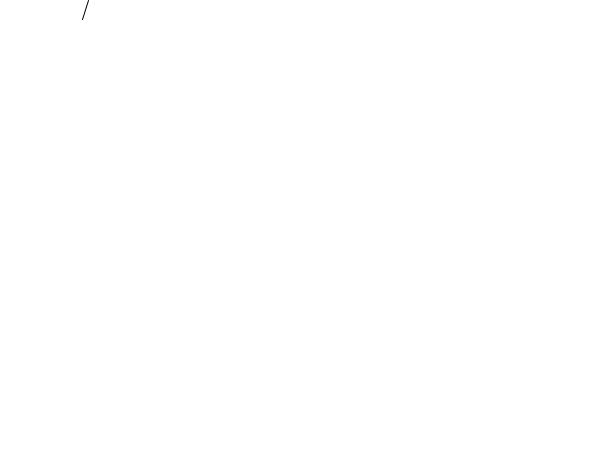
Кинематика прямолинейного движения			7
Lmin = lv1 v2 = 300 м .
	Задача 1.4
Волк преследует зайца, который удирает
от него к норе с постоянной скоростью uG.
Скорость волка vG	постоянна по величине
и направлена все время на зайца, причем
v > u . В начальный момент vG		uG , рас-
стояние между волком и зайцем равно L ,
а расстояние от зайца до норы равно b
(рис.1.4). Найти время погони		τ и наи-
большее начальное расстояние		Lmax , при
котором волк догонит зайца.		рис. 1.4
		Решение

	Обозначим расстояние между участниками погони
	в произвольный момент времени через l		(рис.1.4). За
	последующий бесконечно малый интервал времени
	dt волк сместится на расстояние vdt , заяц – на рас-
	стояние udt , а расстояние между ними станет равным
	l + dl (рис.1.5). Стороны треугольника, изображенно-
	го на рис.1.5, связаны теоремой косинусов:
рис. 1.5	(l −vdt )2 = (l + dl )2 +(udt )2 −2(l + dl )(udt )cos α .

Раскрывая скобки и пренебрегая слагаемыми второго порядка малости,

находим:	−dl = vdt −u cos αdt .
Интегрируя это уравнение с учетом начальных условий, получим
	0	τ
	−∫dl = L = vτ−u∫cos αdt ,		(1.3)
	L	0

где в момент времени t = τ происходит встреча и l = 0 . С другой стороны, в момент встречи x – координаты участников должны быть одинаковы, т.е.

	τ					τ
xвст = ∫vxdt = uτ				или		v∫cos αdt = uτ .			(1.4)
τ	0					0
Исключая ∫cos αdt	из уравнений (1.3) и (1.4), находим время погони τ
0
и координату точки встречи xвст :
τ =		vL	;	x	= uτ =		vuL	.
τ =			;	x	= uτ =			.
		v2 −u2		вст			v2 −u2
		v2 −u2					v2 −u2

8 Глава 1. Кинематика

Так как встреча состоится только, если xвст ≤ b , то максимальное началь-

ное расстояние между волком и зайцем, при котором охота будет успешной, равно

Lmax = b v2 −uu2 .

Прямолинейное ускоренное движение.

Задача 1.5

Космический аппарат при посадке выпускает тормозной парашют, благодаря которому ускорение торможения оказывается пропорциональным квадрату скорости с коэффициентом пропорциональности β=0,02 м–1. При уменьшении начальной посадочной скорости v0 =240 м/с в 100 раз вклю-

чаются тормозные колодки, и аппарат останавливается. Найти время и путь торможения, а также среднюю скорость движения при посадке.

Решение

Согласно условию задачи,	dv	= −βv2 .

	dt

Разделяя переменные и интегрируя это уравнение с учетом начальных условий (v=vo при t=0), получаем:

∫

= −β∫dt,

откуда

−

= βt .

Скорость аппарата меняется со временем по закону v =

. Под-

1+βv t

ставив сюда конечную скорость v = 0, 01 v0

находим время торможения:

t = 99 (βv0 )= 20, 6 c . Теперь вычислим тормозной путь:

v dt

ln (1+βv0t )=

l = ∫vdt = ∫

ln100 = 230 м .

1+βv t

Средняя скорость при торможении, по определению, имеет величину

= l t = (v0 ln100)/ 99 =11, 2

м/с.

Криволинейное ускоренное движение.

Задача 1.6

S = 20 см2 , находящегося на

Из наконечника брандспойта с сечением

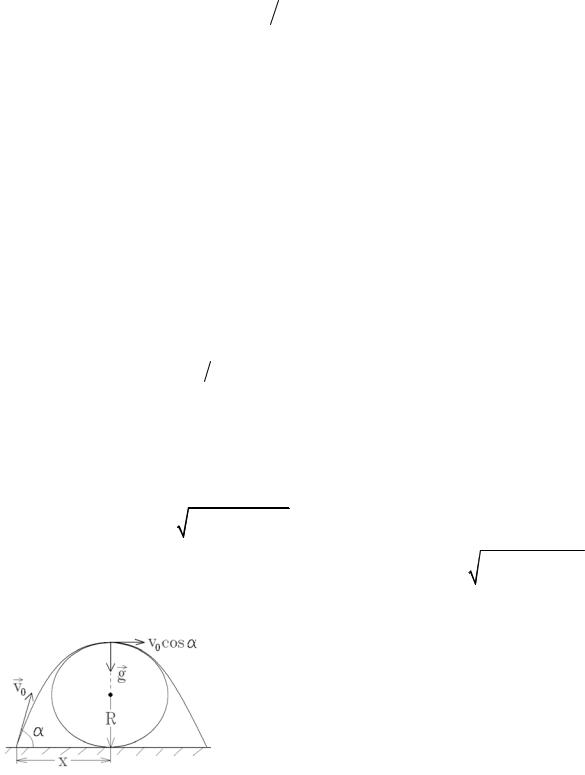
высоте h =1,5 м над землей, со скоростью v0 =15 м/с вырывается струя

воды (рис.1.6). Найти массу воды, висящей в воздухе, если наименьший радиус кривизны струи равен h . Сопротивлением воздуха пренебречь.

Криволинейное ускоренное движение.

Решение.

R = v2

Радиус

кривизны

будет

наименьшим в верхней точке траекто-

рии,

где

скорость струи

v = v0 cos α

минимальна ( α – угол наклона бранд-

спойта к горизонту), а нормальное ус-

рис. 1.6

корение an = g – максимально (рис.1.6).

Отсюда

= h = (v

cos α)2

cosα= gh

v2 .

(1.5)

min

Из кинематического соотношения

y = h +v

sin αt − gt2

2 = 0

можно определить время полета струи до падения на землю:

t =

sin α+

sin

α+2gh g .

Подставляя сюда начальный угол α из формулы (1.5), найдем:

	v	2	− gh +	v	2		g .
t =						+ gh
	0			0

За это время из брандспойта вылетает вода объемом v0 St . Поэтому масса воды, находящейся в воздухе,

ρводыSv0

m = ρ

воды

St =

− gh +

+ gh

= 91,7 кг .

Задача 1.7

На горизонтальной поверхности стоят два забора с высотой h1 и h2. С какой минимальной скоростью v0 следует бросить тело с уровня поверх-

ности, чтобы оно перелетело через оба забора? Расстояние между верхними точками заборов равно l.

рис. 1.7

ность их высот

Решение

Так как v02 = v12 +2gh1 ( v1 – скорость тела у

вершины первого забора (рис.1.7)), то можно искать не минимум v0 , а минимум v1 , что гораздо

проще. Приведенная формула легко выводится как из кинематических соображений, так и из закона сохранения энергии.

Пусть расстояние между заборами равно x , раз- h2 −h1 = y , а в момент пролета над первым забором ско-

10	Глава 1. Кинематика
рость vG	тела составляет угол α с горизонтом (рис.1.7). Элементарные
1

формулы кинематики равноускоренного движения приводят к связям:

x = v	cos α t и y = v sin α t − gt2	2 , где g – ускорение свободного паде-
1	1
ния, t	– время полета между вершинами заборов. Исключая отсюда t ,
приходим к уравнению:				g x2
	y = x tgα−					.
	y = x tgα−		2v	2 cos2		.
			2v	2 cos2	α
		1

Приняв во внимание, что 1/ cos2 α =1+ tg2α и вводя обозначение tgα = ξ ,

находим соотношение между v1				и ξ в неявном виде:
		y = xξ−				gx2	(1+ξ2 ).			(1.6)
		y = xξ−				2v2	(1+ξ2 ).			(1.6)
						1
Дифференцируя формулу (1.6) поξ и учитывая, что x и y										– постоян-
ные величины, получаем:
	gx2 dv				(1+ξ2 )−			gx2
x +			1						ξ = 0 .	(1.7)
x +		v13	dξ					v12	ξ = 0 .	(1.7)
В случае экстремума dv1		dξ = 0 , и поэтому из уравнения (1.7) следует:

ξm = v1m2 gx . Подстановка этого значения ξm в формулу (1.6) дает биквадратное уравнение для определения v1m :

v1m4 −2g y v1m2 − g2 x2 = 0 ,

решение которого позволяет получить искомую величину: v1m2 = g y + g2 y2 + g2 x2 = (y +l )g = (h2 −h1 +l )g .

Следовательно, v0m2

рис. 1.8

= v1m2 +2gh1 или, окончательно, v0m = (h1 +h2 +l )g .

Задача 1.8

Сферический резервуар радиуса R находится на земле. С какой наименьшей скоростью и под каким углом к горизонту следует бросить камень, чтобы он перелетел резервуар?

Решение

Очевидно, что траектория камня должна быть симметричной, а радиус кривизны этой траектории во всех точках должен превышать радиус сферы (рис.1.8). Радиус кривизны

1 / 191 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 > Следующая >>>

Соседние файлы в папке Ю.Н. Колмаков, Ю.А. Пекар, Л.С. И.М. Лагун, Л.С. Лежнева. Механика и теория относительности. Лекции.

#
22.01.20143.9 Mб136mech-lec-TulGU.pdf
#
22.01.20143.32 Mб744mech-zad-TulGU.pdf