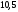- •Министерство образования, науки и молодежной политики Забайкальского края
- •Введение
- •Практическая работа № 1
- •Практическая работа № 2
- •Приближенные вычисления с помощью правил подсчета цифр
- •Приближенные вычисления по способу границ
- •Практическая работа № 3
- •1. Понятие мнимой единицы
- •2. Степени мнимой единицы
- •3. Определение комплексного числа
- •4. Действия над комплексными числами в алгебраической форме
- •Практическая работа № 4
- •Степени и корни
- •Решение иррациональных уравнений
- •1. Выполните действия:
- •2. Решить уравнения:
- •3. Выполните действия:
- •Практическая работа № 5
- •Свойства показательной функции
- •Практическая работа № 6
- •Показательные уравнения
- •Примеры решения показательных уравнений и неравенств
- •Практическая работа № 7
- •2. Определите множество значений функции:
- •Практическая работа № 8
- •Логарифмическое уравнение
- •Логарифмическое неравенство
- •Практическая работа № 9
- •Практическая работа № 10
- •Основные формулы тригонометрии: Синус и косинус сложения аргументов
- •Формулы двойного аргумента (двойного угла)
- •Тангенс сложения аргументов
- •Формулы приведения для тригонометрических функций
- •Практическая работа № 11
- •Практическая работа № 12
- •Решение простейших тригонометрических уравнений
- •Практическая работа № 13
- •1. Уравнения, сводящиеся к квадратам
- •3. Уравнения, решаемые разложением левой части на множители
- •Решение тригонометрических неравенств
- •Практическая работа № 14
- •Практическая работа № 15
- •1. Формулы дифференцирования
- •2. Основные правила дифференцирования
- •Практическая работа № 16
- •Практическая работа № 17
- •Первообразная. Неопределенный интеграл:
- •Практическая работа № 18
- •Вариант 1
- •Вариант 2
- •Практическая работа № 19
- •Вариант 1
- •Вариант 2
- •Практическая работа № 20
- •Практическая работа № 21
- •Практическая работа № 22
- •Практическая работа № 23
- •Практическая работа № 24
- •Практическая работа № 25
- •Практическая работа № 26
- •Практическая работа № 27
- •Практическая работа № 28
- •Элементы комбинаторики
- •Практическая работа № 29
- •Классическое определение вероятности
- •Практическая работа № 30
- •Вариационный ряд и его характеристики
- •Литература
- •Содержание
- •Бронников Анатолий Павлович математика
Практическая работа № 7
Тема: Логарифм числа. Логарифмическая функция и её свойства
Цель работы: закрепить знания и умения студентов по освоению логарифмов и свойств логарифмической функции.
Теоритическое обоснование:
Основные свойства логарифмов
Сложение и вычитание логарифмов
loga x + loga y = loga (x · y);
loga x − loga y = loga (x : y).
Вынесение показателя степени из логарифма
logaxn=n· logax;
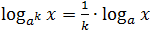
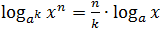
Переход
к новому
основанию
![]()
В частности,
если положить c = x,
получим:
![]()
Основное логарифмическое тождество
Часто в процессе решения требуется представить число как логарифм по заданному основанию. В этом случае нам помогут формулы:
n = loga an
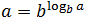
Логарифмическая единица и логарифмический ноль
loga a = 1 — это логарифмическая единица. Запомните раз и навсегда: логарифм по любому основанию a от самого этого основания равен единице.
loga 1 = 0 — это логарифмический ноль. Основание a может быть каким угодно, но если в аргументе стоит единица — логарифм равен нулю! Потому что a0 = 1 — это прямое следствие из определения.
2. Логарифмическая функция.
Определение. Функцию, заданную формулой y =logax, называют логарифмической функцией с основанием а.
1. Область определения логарифмической функции — множество всех положительных чисел R+, т. е. D(loga)=R+. 2. Область значений логарифмической функции — множество всех действительных чисел.
3. Логарифмическая функция на всей области определения возрастает (при а>1) или убывает (при 0<а<1).
Для построения графика заметим, что значение 0 логарифмическая функция принимает в точке 1; loga 1 =0 при любом а>0, так как а0 = 1.
Вследствие возрастания функции при а>1 получаем, что при х>1 логарифмическая функция принимает положительные значения, а при 0<a<1—отрицательные. Если 0<а<1, то y=logax убывает на R+, поэтому loga x>0 при 0<x<1 и logax<0 при х>1.
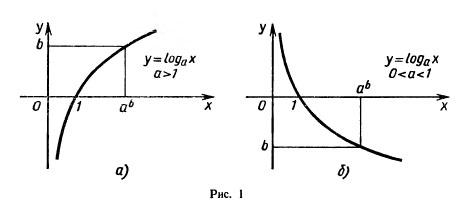 Опираясь
на доказанные свойства, нетрудно
построить график функции y
= loga х
при а>1 (рис. 1, а) и0<а<1 (рис. 1,б).
Опираясь
на доказанные свойства, нетрудно
построить график функции y
= loga х
при а>1 (рис. 1, а) и0<а<1 (рис. 1,б).
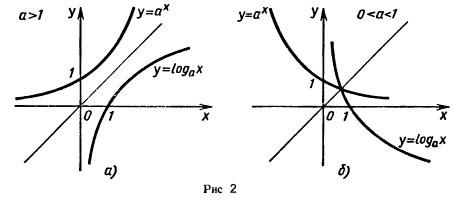
Справедливо следующее утверждение: Графики показательной и логарифмической функций, имеющих одинаковое основание, симметричны относительно прямой у = х
Текст задания
Выполните действия:
|
Свойства логарифмов Вариант 1 | ||
|
А) Выберите номер правильного ответа | ||
|
А1 |
Вычислите:
|
1)
|
|
А2 |
Упростите:
|
1)
|
|
А3 |
Вычислите:
|
1)
|
|
А4 |
Найдите
значение выражения:
|
1)
|
|
А5 |
Найдите
значение выражения:
|
1)
|
|
А6 |
Вычислите:
|
1)
|
|
А7 |
Найдите
значение выражения:
|
1)
|
|
А8 |
Вычислите
|
1)
|
|
Свойства логарифмов Вариант 2 | ||
|
А) Выберите номер правильного ответа | ||
|
А1 |
Вычислите:
|
1)
|
|
А2 |
Упростите:
|
1)
|
|
А3 |
Вычислите:
|
1)
|
|
А4 |
Найдите
значение выражения:
|
1)
|
|
А5 |
Найдите
значение выражения:
|
1)
|
|
А6 |
Вычислите:
|
1)
|
|
А7 |
Найдите
значение выражения:
|
1)
|
|
А8 |
Вычислите
|
1)
|
|
Свойства логарифмов Вариант 3 | ||
|
А) Выберите номер правильного ответа | ||
|
А1 |
Вычислите:
|
1)
|
|
А2 |
Упростите:
|
1)
|
|
А3 |
Вычислите:
|
1)
|
|
А4 |
Найдите
значение выражения:
|
1)
|
|
А5 |
Найдите
значение выражения:
|
1)
|
|
А6 |
Вычислите:
|
1)
|
|
А7 |
Найдите
значение выражения:
|
1)
|
|
А8 |
Вычислите
|
1)
|
|
Свойства логарифмов Вариант 4 | ||
|
А) Выберите номер правильного ответа | ||
|
А1 |
Вычислите:
|
1)
|
|
А2 |
Упростите:
|
1)
|
|
А3 |
Вычислите:
|
1)
|
|
А4 |
Найдите
значение выражения:
|
1)
|
|
А5 |
Найдите
значение выражения:
|
1)
|
|
А6 |
Вычислите:
|
1)
|
|
А7 |
Найдите
значение выражения:
|
1)
|
|
А8 |
Вычислите
|
1)
|

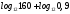
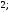 2)
2)
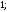 3)
3)
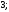 4)
4)
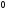
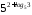
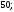 2)
2)
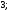 3)
3)
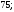 4)
4)
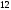
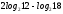
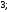 2)
2)
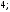 3)
3)
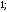 4)
4)
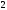
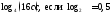
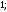 2)
2)
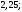 3)
3)
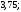 4)
4)
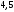
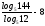
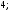 2)
2)
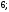 3)
3)
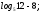 4)
4)
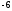
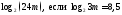
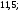 2)
2)
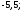 3)
3)
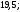 4)
4)
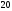
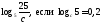
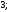 2)
2)
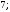 3)
3)
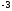 4)
4)
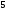
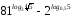
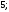 2)
2)
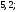 3)
3)
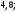 4)
4)
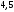
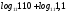
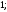 2)
2)
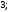 3)
3)
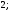 4)
4)
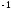
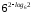
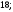 2)
2)
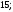 3)
3)
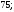 4)
4)
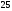
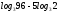
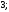 2)
2)
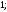 3)
3)
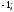 4)
4)
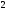
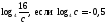
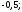 2)
2)
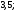 3)
3)
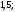 4)
4)
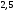
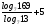
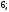 2)
2)
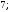 3)
3)
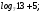 4)
4)
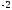
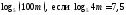
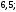 2)
2)
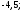 3)
3)
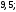 4)
4)
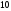
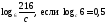
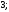 2)
2)
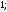 3)
3)
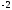 4)
4)
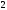
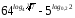
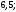 2)
2)
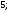 3)
3)
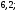 4)
4)
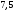
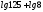
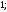 2)
2)
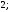 3)
3)
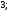 4)
4)
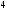
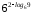
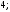 2)
2)
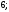 3)
3)
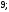 4)
4)
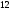
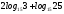
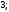 2)
2)
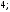 3)
3)
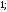 4)
4)
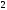
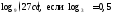
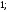 2)
2)
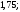 3)
3)
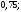 4)
4)
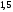
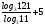
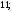 2)
2)
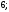 3)
3)
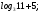 4)
4)
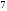
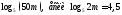
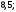 2)
2)
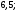 3)
3)
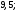 4)
4)
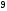
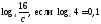
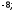 2)
2)
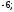 3)
3)
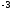 4)
4)
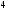
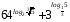
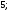 2)
2)
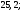 3)
3)
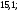 4)
4)
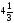
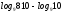
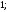 2)
2)
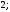 3)
3)
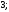 4)
4)
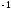
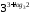
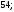 2)
2)
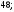 3)
3)
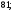 4)
4)
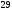
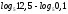
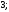 2)
2)
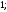 3)
3)
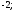 4)
4)
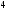
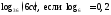
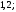 2)
2)
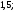 3)
3)
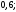 4)
4)
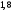
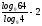
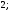 2)
2)
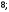 3)
3)
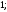 4)
4)
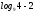
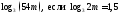
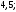 2)
2)
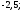 3)
3)
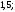 4)
4)
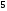
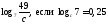
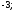 2)
2)
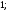 3)
3)
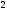 4)
4)
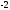
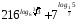
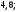 2)
2)
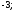 3)
3)
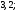 4)
4)