
- •Оглавление
- •ОБЩИЕ СВЕДЕНИЯ
- •1. СТРУКТУРА САМОСТОЯТЕЛЬНОЙ РАБОТЫ
- •2. ИЗУЧЕНИЕ ТЕОРЕТИЧЕСКОГО МАТЕРИАЛА
- •3. РЕШЕНИЕ ЗАДАЧ
- •4. ПОДГОТОВКА К ВЫПОЛНЕНИЮ ЛАБОРАТОРНЫХ РАБОТ
- •6. МЕТОДИКА ПРИМЕНЕНИЯ КРЕДИТНО-РЕЙТИНГОВОЙ СИСТЕМЫ
- •7. МЕТОДИКА ПРОВЕДЕНИЯ ПРОМЕЖУТОЧНОЙ АТТЕСТАЦИИ
- •БИБЛИОГРАФИЧЕСКИЙ СПИСОК
- •Основной
- •Дополнительный
- •ПРИЛОЖЕНИЯ

3. РЕШЕНИЕ ЗАДАЧ
Методические указания. Решение любой задачи начинают с записи в общем виде необходимых уравнений гидромеханики или газовой динамики, в каждом конкретном случае размерность берут ту, которая наиболее удобна.
Исходные уравнения желательно привести к наиболее простому виду. Так, в соответствии с условиями задачи следует взаимно уничтожить одинаковые члены в правой и левой части соответствующего исходного уравнения, а также определять численные значения отдельных величин, непосредственно входящих в это уравнение. Например, в правой части уравнения Бернулли абсолютное давление P2 , равно атмосферному Pа , а в левой части этого
уравнения абсолютное давление P1 больше атмосферного и по условию задачи известно избыточное давление, соответствующее абсолютному P1 . В этом
случае целесообразно абсолютное давление P записать так: |
P |
= P + P |
, а P |
1 |
1а |
изб |
а |
в правой и левой части уравнения Бернулли сократить. Другой пример: членом того же уравнения Бернулли является динамическое давление ρV 2 / 2 , а по условию задачи известен расход и площадь сечения (Q и F ). Здесь можно в исходное уравнение ввести численное значение скорости, предварительно определив eгo по формуле V =Q / F . Если вместо ρV 2 / 2 ввести выраже-
ние ρQ2 / 2F 2 , расчеты значительно усложнятся.
Решение задачи должно быть доведено до цифрового ответа в соответствующей размерности. Решение записывают в алгебраической форме, вместо букв проставляют соответствующие цифры и приводят окончательный цифровой ответ без каких-либо промежуточных вычислительных операций. Лишь в отдельных случаях, определяемых условиями задачи, решение ее может быть выполнено в общем виде.
Все контрольные задачи следует решать в системе СИ.
В производственных и лабораторных условиях давление может измеряться в различных единицах (кг/см2; кг/м2; м вод. ст.; мм вод. ст.; мм вод. ст.; мм рт. ст. и др.) , поэтому необходимо знать соотношения между различными единицами измерения давления и уметь переводить одни единицы в другие.
Решению большинства задач помогает чертеж-схема с плоскостью сравнения, плоскостью ровного давления, нивелирными высотами, определяющими положение характерных точек. Кроме того, на чертеже должны быть показаны сечения, к которым при решении задачи применены те или другие уравнения.
Эти сечения обозначают соответствующими цифрами (1, 2 и т. д.). Давление, скорость, плотность, температуру и др. параметры каждого такого сечения обозначают буквами и индексами по нумерации сечения.
Гидрогазодинамика. Метод. указания к самостоятельной работе |
12 |

3. РЕШЕНИЕ ЗАДАЧ
При решении большинства задач по гидромеханике необходимо строить напорные и пьезометрические линии, по которым можно проследить, как изменяются полное давление или полный напор и статическое давление или гидростатический напор в том или ином сечении потока, перемещающегося по трубопроводу или газопроводу. Эти линии строят на чертеже-схеме.
Физические свойства жидкости. Основными физическими свойства-
ми жидкостей являются плотность, сжимаемость, вязкость и поверхностное натяжение.
Плотностью ρ , кг/м3, называется масса однородной жидкости, содержащейся в единице объема:
ρ = Vm ,
где m – масса жидкости, кг; V – объем жидкости, м3.
Плотность газов можно определять по уравнению состояния:
ρ = p R T ,
R T ,
где p – давление, Па; R – удельная газовая постоянная, Дж/(кг·K); T – термодинамическая температура, K.
Объемным (удельным) весом жидкости, γ , Н/м3, называется вес еди-
ницы объема этой жидкости:
γ = VG ,
где G – вес жидкости, Н; V – объем жидкости, м3. Плотность и удельный вес связаны соотношением
γ = ρ g,
где g – ускорение свободного падения, м/с2.
Сжимаемость – свойство жидкости (газа) изменять свой объем под воздействием внешних сил. Сжимаемость оценивается коэффициентом сжимаемости βp, Па-1:
βp = V∆∆Vp ,
где V – начальный объем, м3; ∆V – изменение объема, м3; ∆p – изменение
давления, Па.
Тепловое расширение – свойство жидкости изменять объем при нагревании, характеризуется коэффициентом теплового расширения βt , ºС-1:
Гидрогазодинамика. Метод. указания к самостоятельной работе |
13 |

3. РЕШЕНИЕ ЗАДАЧ
βt = V∆∆VT ,
где ∆T – изменение температуры, ºС.
Вязкость жидкости – способность жидкости сопротивляться относительному скольжению ее слоев. Вязкость характеризуется коэффициентом кинематической ν , м2/с, и динамической вязкости µ, Па·с, которые связаны
соотношением
ν=µρ.
Поверхностным натяжением называется свойство жидкости образовывать поверхностный слой взаимно притягивающихся молекул. Характеризуется коэффициентом поверхностного натяжения σ, Н/м, равным силе F на единице длины контура свободной поверхности L:
σ= FL .
Распространенные системы измерения единиц физических величин – СИ и МКГСС. Соотношения между наиболее употребительными единицами измерения приведены в прил. 1.
Пример решения задач
Теплоснабжение района осуществляется по двухтрубному теплопроводу (рис. 3.1) с внутренним диаметром труб dв = 400 мм и длиной l = 1000 м.
Расход сетевой воды Qс = 500 м3/ч. Расход подпиточной воды при температуре воды в сети 95 °С, Qпв = 5 м3/ч, температурный коэффициент объемного расширения воды βt = 0,0006 °С-1. Определить расход подпи-
точной воды, если в течение 1 ч производится равномерное повышение температуры воды Т в теплообменнике от 70 до 95 °С при неизменном давлении в сети.
Рис. 3.1
Гидрогазодинамика. Метод. указания к самостоятельной работе |
14 |

3. РЕШЕНИЕ ЗАДАЧ
Решение
Определим объем воды в подающем трубопроводе:
Vтр = Fl = πd4 2 l ,
Vтр = 3,1440,42 4000 = 502 м2.
Так как часовой расход воды меньше объема подающего трубопровода, то вода с температурой 95°С в течение 1 ч не успеет поступить к потребителям и охладиться.При среднем повышении температуры воды в подающем трубопроводе на
∆t = 95 −2 70 =12,5 °С
произойдет увеличение объема воды на величину
∆V =βt ∆TVтр ,
∆V = 6 10−4 12,5 502 =3,76 м3.
Таким образом, расход подпиточной воды в течение времени повышения температуры будет равен
Qпвt = Qпв − ∆tV ,
Qпвt = 5 − 3,176 =1,24 м3/ч.
Задания
1.1. Плотность морской воды ρ = 104,8 кгс·с2/м4. Определить ее удельный вес γ.
Ответ: γ= 1028,1 кгс/м3 = 10085,7 Н/м3.
1.2. Определить удельный вес смеси жидкостей γсм, имеющей сле-
дующий состав: керосина 40 %, мазута 60 % (проценты весовые), если удельный вес керосина γ1= 790 кгс/м3, мазута γ2 = 890 кгс/м3.
Ответ: γсм = 845 кгс/м3 = 8289 н/м3.
1.3. При нормальных условиях, т.е. при t = 0 °С и давленииhσ = 760 ммрт. ст., плотность кислорода ρ = 0,1457 кгс·с2/м4.
Определить его плотность при температуреt = – 60 °С и том же давлении. Ответ: ρ = 0,187 кгс·с2/м4 = 1,84 кг/м3.
1.4. Нефть, имеющая удельный вес γ= 9·103 Н/м3, обладает при температуре t = 50 °С вязкостью µ= 6,0·10–4 кгс·с/м2 = 5,884·10–4 Н∙с/м.
Определить ее кинематическую вязкость ν .
Гидрогазодинамика. Метод. указания к самостоятельной работе |
15 |

3. РЕШЕНИЕ ЗАДАЧ
Ответ: ν = 6,4·10–2 см2/с = 6,0·10–6 м2/с.
1.5. Кинематическая вязкость нефти при температуре t = 10 °С составляет 12·10–6 м2/с. Определить динамическую вязкость µ, если при темпера-
туре t = 20 °С плотность нефтиρ = 890 кг/м3.
Ответ: µ= 0,001089 кгс·с/м2 = 0,01068 Н∙с/м2.
1.6. При экспериментальном определении вязкости нефти вискозимет-
ром Энглера найдено: время истечения 200 см3 воды τ1= 51,2 с, время истечения 200 см3 нефти τ2 = 163,4 с. Определить кинематическую вязкость нефти.
Ответ: ν = 0,213 см2/с.
1.7. В автоклав объемом V = 50 л под некоторым давлением закачано 50,5 л эфира. Определить, пренебрегая деформацией стенок автоклава, по-
вышение давления в нем ∆P , если коэффициент объемного сжатия эфира при t = 20 °С β= 1,91·10–4 cм2/кгс = 1,95·10–9 м2/Н.
Ответ: ∆P = 52,4 кгс/см2 = 51,4·105 Н/м2.
1.8. На какую величину переместится шток гидроцилиндра диаметром D с запертым в нем при атмосферном давлении объемом минерального масла
V0 = 18 л, если |
на шток приложить усилие Т. Значения D и Т указаны |
||||||||||
в табл. 3.1. Коэффициент сжимаемости масла βP = 6,6·10–10 м2/Н. Деформацией |
|||||||||||
стенок гидроцилиндра пренебречь. |
|
|
|
|
Таблица 3.1 |
||||||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||
Параметр |
|
|
|
|
Вариант |
|
|
|
|
||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
||
|
|||||||||||
D, мм |
50 |
56 |
63 |
70 |
80 |
90 |
100 |
110 |
125 |
140 |
|
Т, 104 Н |
3,5 |
4,5 |
5,0 |
6,0 |
8,0 |
10,0 |
12,0 |
15,0 |
19,0 |
24,0 |
|
1.9. При температуре 20 °С масло М-10-В2 занимает объём V0, указанный в табл. 1.2. Определить объём, который оно будет занимать при температуре минус 40 °С и 80 °С, если температурный коэффициент объёмного расширения масла βt = 8,75·10–4 °С-1.
Таблица 3.2
Объем масла |
|
|
|
|
Вариант |
|
|
|
|
||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
||
|
|||||||||||
V, л |
25 |
50 |
75 |
100 |
125 |
150 |
175 |
200 |
225 |
250 |
|
1.10. Определить плотность рабочих жидкостей при различных температурах. Температурный коэффициент объёмного расширения всех масел βt =
8,75·10–4 °С-1. Значения ρ20 при температуре 20 °С этих масел даны в прил. 2.
1.11. Уровень мазута в вертикальном цилиндрическом баке диаметром 2 м за некоторое время понизился на 0,5 м. Определить количество израсходованного мазута, если плотность его при температуре окружающей среды 20 °С равна ρ= 990 кг/м3.
1.12. Стальной барабан подвергается гидравлическому испытанию под избыточным давлением 2 Мпа. Определить, какое количество воды дополни-
Гидрогазодинамика. Метод. указания к самостоятельной работе |
16 |

3. РЕШЕНИЕ ЗАДАЧ
тельно к первоначальному объёму при атмосферном давлении необходимо подать насосом в барабан, если его геометрическая ёмкость равна 10 м3. Деформацией барабана пренебречь, коэффициент объёмного изотермического сжатия воды β = 1/2·10–9 Па.
1.13. Определить объём расширительного сосуда Vpc, который необходимо установить в системе водяного отопления с объёмом воды V0, если известно, что максимальная разность температур воды в подающем и обратном трубопроводах 25 °С. Запас по объёму расширительного сосуда принять трёхкратным. Температурный коэффициент объёмного расширителя воды
βt = 0,0006 °С-1.
1.14.По условиям гидравлического испытания водопровода диаметром
d = 200 мм и длиной l = 1000 м давление должно быть поднято от атмосферного до 2 Мпа. Определить объем воды, который потребуется дополнительно
подать в водопровод. Деформацией труб пренебречь.
Ответ: ∆V = 31,4·10–3 м3.
1.15. Определить изменение объёма 27 т нефтепродукта в хранилище при колебании температуры от 20 до 50 °С, если при t = 20 °С плотность нефтепродукта равна ρ20 = 900 кг/м3, а температурный коэффициент объёмно-
го расширения βt = 0,001 °С-1.
1.16. Предельная высота уровня мазута в вертикальной цилиндрической цистерне равна h0 = 10 м при температуре 0°С. Определить, до какого уровня можно налить мазут, если температура окружающей среды повысится до 35 °С. Расширением цистерны пренебречь, температурный коэффициент объёмного расширения для мазута принять равным βt = 0,001 °С-1.
1.17. Определить массовую теплоёмкость ср генераторного газа при температуре 0°С, если его объёмный состав: хH2 = 18 %; хco = 24 %; хco2 = 6 %; хN 2 = 52 %. Зависимость теплоёмкости от температуры не учитывать.
Гидростатика. Гидростатическим давлением р, Н/м2, называется си-
ла, действующая на единицу площадки по нормали к поверхности. Гидростатическое давление жидкости складывается из давления на ее
свободную поверхность p0 и давления столба жидкости, высота которого h, м, равна расстоянию от этой точки до свободной поверхности:
p = p0 + ρgh ,
где ρ – плотность жидкости, кг/м3; g – ускорение свободного падения, м/с2.
Гидростатическое давление называется абсолютным (pабс), а величина ρgh – избыточным давлением (если на свободную поверхность жидкости действует атмосферное давление), т. е.
pабс = pизб + pатм ,
Гидрогазодинамика. Метод. указания к самостоятельной работе |
17 |

3. РЕШЕНИЕ ЗАДАЧ
Абсолютное давление меньше атмосферного называют вакуумным:
pатм − pабс = −pизб = pвак ,
Полная сила, действующая на плоскую стенку h, равна произведению смоченной площади стенки F, м2, на гидростатическое давление в ее центре тяжести:
P = (p0 +ρghцт )F ,
где hцт – глубина погружения центра тяжести, м.
Полная сила, действующая на цилиндрическую поверхность:
P = 
 Px2 + Py2 ,
Px2 + Py2 ,
где PX – горизонтальная составляющая, равная силе давления жидкости на вертикальную проекцию цилиндрической поверхности, Fвepm:
Px = ρghцтFверт ,
PY – вертикальная составляющая силы давления Р, равная силе тяжести, действующей в объеме тела V:
Py = ρgV .
Направление полной силы давления Р определяется:
tg α = Py .
Px
На любое тело, погруженное в жидкость, действует выталкивающая сила, равная весу жидкости, вытесненной телом (закон Архимеда):
P = ρgV ,
где Р – выталкивающая (архимедова) сила, Н; ρ – плотность жидкости, кг/м3; g
– ускорение свободного падения, м/с2; V – объем погруженной части тела, м3. Произведение ρgV называют водоизмещением.
Пример решения задач
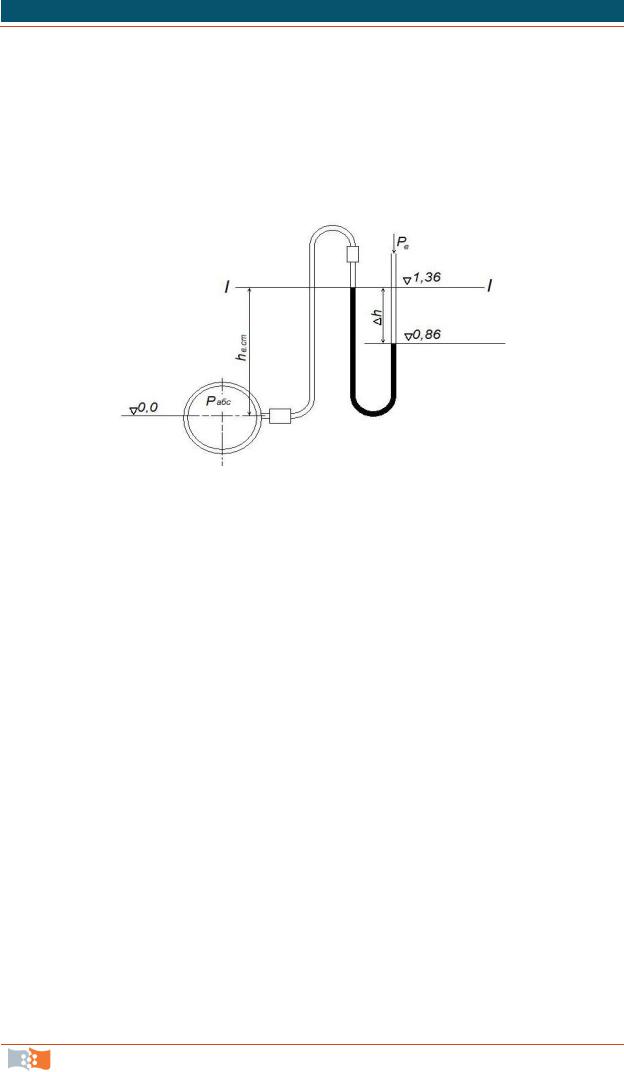
Для измерения давления газа в баллоне применен двухжидкостный чашечный манометр, диаметры чашечек которого одинаковы и равны D, а диа-
Гидрогазодинамика. Метод. указания к самостоятельной работе |
18 |

3. РЕШЕНИЕ ЗАДАЧ
метр трубок – d. Манометр заполнен ртутью (плотность ρрт = 13600 кг/м3) и водой, объем которой одинаков в правой и левой частях манометра (рис. 3.2). Определить абсолютное давление газа в баллоне и вакуум, если разность уровней ртути h = 20 см, отношение d/D = 0,l, плотность воды ρ = 1000 кг/м3,
атмосферное давление pа = 750 мм рт. ст.
Решение
Вода и ртуть в манометре находятся в равновесии под действием давлений pа и p на поверхности воды в чашечках манометра. Пренебрегая изменением давления в столбе газа (ввиду малости его плотности), считаем давление p равным давлению газа в баллоне. Применим уравнение гидростатики, запишем его в виде
р = p0 + ρgh .
Прежде всего определим плоскость, в которой в правой и левой трубках манометра давления будут одинаковыми. Такой горизонтальной плоскостью является плоскость I–I, давление которой обозначим через p1. Это давление справа (согласно основному закону гидростатики) определяется атмосферным давлением pа на поверхности воды в правой чашечке манометра и давлением, которое создает столб воды высотой h1 + h, т. е.
р1 = pа + ρg(h1 + h).
Давление p1 слева уравновешивается давлением p на поверхности воды в левой чашечке манометра, давлением, создаваемым столбом воды высотой ∆h + h1, и давлением, которое создает столб ртути высотой h. Таким образом,
P1 = pа + ρg(∆h + h1 )+ ρрт gh .
Из этих уравнений получим
pа + ρg∆h + ρgh1 + ρрт gh = pа + ρgh1 + ρgh .
Рис. 3.2
Гидрогазодинамика. Метод. указания к самостоятельной работе |
19 |

3. РЕШЕНИЕ ЗАДАЧ
Сократив на pgh1 правую и левую части уравнения, определим давление p газа в баллоне:
p = pа + (p − pрт )gh −ρg∆h .
Превышение уровня воды в левой чашечке манометра ∆h над уровнем в правой определим из условия равенства объемов воды в правой и левой частях манометра:
πD2∆h = πd 2h
откуда
∆h=h(d/D)2
Δh=0,2(1/10)2=0,002 м.
Атмосферное давление pа, выраженное по условию задачи в мм рт. ст., переведем в Н/м2 :
pа = g 10150 Н/м2.
Определим численное значение давления газа в баллоне:
p = g [10150 +0,2(1000 −13600)−1000 0,002]= 76,5 кПа.
Разрежение в баллоне (вакуум):
pвак = pа − p = gh(ρрт −ρ)+ρg∆h
pвак = [0,2(13600 −1000)+1000 0,002]g = g2520 Н/м2 = 25 кПа.
Ответ: р = 76,5 кПа; pвак = 25 кПа.
Задания
2.1. Определить давление воды на корпус подводной лодки при погружении на глубину 50 м.
Ответ: ризб = 0,49 МПа.
2.2. Определить величину избыточного гидроста-
тического давления ра в точке А под поршнем и рв |
в |
точке В воды на глубине z = 2 м от поршня, если на |
|
поршень диаметром d = 200 мм производится давление |
|
силой p = 314 кгс (рис. 3.3). |
|
Ответ: ра = 1 кгс/см2; рв = 1,2 кгс/см2. |
Рис. 3.3 |
2.3. Определить давление р в котле с водой и пье-
зометрическую высоту z1, если высота поднятия ртути в трубке манометра z
Гидрогазодинамика. Метод. указания к самостоятельной работе |
20 |

3. РЕШЕНИЕ ЗАДАЧ
= 50 мм (рис. 3.4).
Ответ: z1 = 0,68 м; р = 0,068 атм.
2.4. В ртутном вакуумметре, подключенном к камере конденсатора паровой машины, столб ртути в ближайшем к нему колене выше, чем в другом, на 600 мм. Барометрическая высота hб = 755 мм рт. ст. (рис. 3.6). Определить разрежение и абсолютное давление в конденсаторе.
Ответ: Разрежение рр = 0,816 кгс/см2; абсолютное давление
ра= 0,210кгс/см2.
2.5. В печи А дымовые газы имеют в среднем температуру t2 = 300 °С и удельный вес γ2 = (1,25 – 0,0027t2) кгс/м3. Температура наружного воздуха tВ
= = 14 °С, давление hб = 760 мм рт. ст. (рис. 3.7). Определить при высоте дымовой трубы Н = 5 м разность напоров ∆Н по обе стороны печной дверки В, если ее закрыть.
Ответ: ∆Н = 3,95 мм вод. ст.
Рис. 3.4 |
Рис. 3.5 |
2.6. Для измерения высоты полета на аэростате применяется точный барометр. Перед вылетом баро-
метр показывал давление h1 = 745 мм рт. ст., а в наи-
высшей точке подъема – давление h2 = 500 мм рт. ст.
Считая температуру воздуха по всей высоте постоянной и равной t = 10 °С, определить высоту подъема аэростата Н.
Ответ: Н = 3300 м.
2.7. Подпорная прямоугольная вертикальная стенка шириной b = 200 м сдерживает напор воды высотой Н = 10 м (рис. 3.7). Определить силу полного давления Р на стенку и опрокидывающий момент
Рис. 3.6 М. Построить эпюру давлений.
Ответ: Р = 10000·103 кгс; М = 33333·103 кгс·м.
Гидрогазодинамика. Метод. указания к самостоятельной работе |
21 |

3. РЕШЕНИЕ ЗАДАЧ
Рис. 3.7
2.8. Определить силу Р полного давления воды на плоскую трапецеидальную стенку, имеющую размеры h = l,8 м,b = 26 м,В= 32 м, α= 45o (рис. 3.8), если удельный вес жидкости γ= 1000 кг/м3.
Ответ: Р = 45,4·103 кгс; zцд = 1,18 м.
2.9. Манометр, установленный на водопроводе, показывает давление 2 кгс/см2. Определить, чему равно абсолютное давление, измеренное в Па, м вод. ст. и мм рт. ст. Атмосферное давление принять равным рат = 1 кгс/см2.
Рис. 3.8 |
|
2.10. Определить разрежение, создаваемое |
|
дымовой трубой, если известно, что высота трубы |
|
50 м, средняя температура уходящих газов 227 °С, |
|
температура окружающего воздуха 27 °С. Плотности |
|
газов и воздуха при 0 °С и 760 мм рт. ст. соответст- |
|
венно равныρг = 1,27 кг/м3; ρв = 1,29 кг/м3. |
|
2.11. Вначале в U-образную трубку налили |
|
ртуть, а затем в одно колено трубки воду, а в другое |
|
бензин (рис. 3.9). При совпадении верхних уровней |
|
бензина и воды высота столба воды равна 43 см. |
|
Определить разность уровней ртути. Плотность |
|
ртути ρрт= 13,6·103кг/м3, плотность бензина |
Рис. 3.9 |
б= 0,7·103кг/м3.
2.12.Определить абсолютное давление воды в трубопроводе, если U-образный ртутный манометр, подключенный по схеме (рис. 3.10), показал перепад ∆h = 500 мм рт. ст. Барометрическое давление 760 мм рт. ст.
2.13.Определить разность давлений в подающей и обратной трубах
Гидрогазодинамика. Метод. указания к самостоятельной работе |
22 |
3. РЕШЕНИЕ ЗАДАЧ
системы водяного отопления, если разность уровней ртути в U-образном манометре ∆h = 500 мм. Трубы расположены в одной горизонтальной плоскости. Ответ дать в Па, мм рт. ст. и в м вод. ст.
2.14.Определить уровень мазута в баке, если при замере S-образной трубкой разность уровней ртути ∆h = 250 мм. Плотность мазута ρм=860кг/м3.
2.15.Прямоугольный открытый резервуар предназначен для хранения 30 м3. Определить силы давления на стенки и дно резервуара, если ширина дна 3 м, а длина 5 м.
Рис. 3.10
2.16.Определить силу давления воды на дно сосуда, если площадь дна его 0,25 м2, а уровень воды расположен на высоте 2 м от дна.
2.17.Дизельное топливо хранится в цилиндрической ёмкости высотой 8 м и д иаметром 5 м. Определить силу, действующую на боковую стенку
хранилища. Плотность дизельного топлива ρ= 860 кг/м3.
2.18.Определить абсолютное давление, если показание вакуумметра равно 50 кПа при барометрическом давлении 100 кПа.
2.19.Определить давление, которое испытывает стенка сосуда, заполненного водой, на глубине h = l м от поверхности.
2.20.Определить горизонтальную силу, действующую на плотину
(рис.3.11) длиной L = 1000 м при высоте воды перед плотиной Н1 = 100 м, а за плотиной Н2 = 10 м.
2.21.Два цилиндра соединены трубкой по схеме, изображенной на рис.
3.12. Известно, что диаметр первого цилиндра D1 = 50 см, а второго – D2 = 20 см. Цилиндр меньшего диаметра расположен выше цилиндра большего диа-
метра на h = 0,5 м. Определить, какое усилие Р1 необходимо приложить к большому поршню, чтобы система пришла в равновесие, если на поршень малого цилиндра действует сила Р2 = 500 Н.
Гидрогазодинамика. Метод. указания к самостоятельной работе |
23 |

3. РЕШЕНИЕ ЗАДАЧ
Рис. 3.11
Рис. 3.12
2.22.Определить абсолютное давление воздуха р0 на поверхности воды
врезервуаре А и высоту поднятия воды в закрытом пьезометре h, присоеди-
ненном к этому резервуару, если показания ртутного вакуумметра hрт, а а т- мосферное давление ра (табл. 3.3)
Таблица 3.3
Величина |
|
|
|
|
Вариант |
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
hрт, мм |
300 |
310 |
320 |
330 |
340 |
350 |
360 |
370 |
380 |
400 |
p0, мм рт. |
733 |
735 |
738 |
740 |
745 |
748 |
750 |
755 |
758 |
760 |
|
|
|
|
|
|
|
|
|
|
|
2.23. Для передачи наверх и контроля уровня топлива в открытом подъемном резервуаре использован U-образный пьезометр, заполненный ртутью, плотность которой ρрт = 13,6 т/м3. Определить высоту столба ртути h2, если разность уровней топлива в указателе и резервуаре h. Как изменится уровень в указателе при понижении уровня топлива в резервуаре на ∆h (табл. 3.4).
Таблица 3.4
Величи- |
|
|
|
|
Вариант |
|
|
|
|
|
|
на |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
9 |
10 |
ρрт, т/м3 |
0,72 |
0,75 |
0,79 |
0,85 |
0,89 |
0,85 |
0,79 |
0,75 |
|
0,73 |
0,72 |
h, м |
8 |
7 |
6 |
5 |
4 |
4 |
5 |
5 |
|
6 |
6 |
∆h, м |
2,0 |
2,0 |
1,5 |
1,5 |
1,0 |
1,0 |
1,5 |
1,5 |
|
2,0 |
2,0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Гидрогазодинамика. Метод. указания к самостоятельной работе |
|
24 |
||||||||

3. РЕШЕНИЕ ЗАДАЧ
Примечание. Высота столба топлива в правом колене пьезометра считается неизменной при любом положении топлива в резервуаре (рис. 3.13).
2.24. Определить необходимую высоту дымовой трубы для печей термического цеха, если труба должна создавать разрежение h мм вод. ст. при средней температуре дымовых газов tг °C и температуре окружающего воздуха tв °С (табл. 3.5). Плотности дымовых газов и воздуха при нормальных ус-
ловиях (to = 0°С и ро = 760 мм рт. ст.) принять соответственно равными ρг, кг/м3 и ρв = 1,293 кг/м3.
|
pa |
pa |
h |
h |
Топливо |
|
h1 |
|
h2 |
Рис. 3.13
Таблица 3.5
Величина |
|
|
|
|
Вариант |
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
рг, кг/м3 |
1,25 |
1,26 |
1,27 |
1,28 |
1,29 |
1,28 |
1,27 |
1,26 |
1,25 |
1,24 |
h, мм вод ст. |
22 |
24 |
26 |
28 |
30 |
32 |
34 |
36 |
38 |
40 |
tг, °C |
320 |
340 |
360 |
380 |
400 |
420 |
440 |
460 |
480 |
500 |
tв, °C |
20 |
22 |
24 |
26 |
28 |
30 |
28 |
26 |
24 |
22 |
Рис. 3.14
Рис. 3.15
Примечание. Разрежение у основания трубы создается за счет разности давления столба атмосферного воздуха и давления столба дымовых газов, равных высоте дымовой трубы Н.
2.25. Определить силу Р полного давления на торцевую плоскую стенку горизонтальной цилиндрической цистерны диаметром D = 2,2 м, если уровень бензина удельного веса γ= 720 кгс/м3 в цис-
терне находится на расстоянии Н = 2,4 м от дна (рис. 3.15). Цистерна герметически закрыта, и избыточное давление паров бензина на свободную поверхность составляет hб = 367 мм рт. ст.
Ответ: Р = 22,5·103 кгс; zцд = 1,337 м.
2.26. Определить силы, растягивающие горизонтальную цистерну, заполненную жидкостью удельным весом γ= 950 кгс/м3, по сечениям АА и
ВВ; диаметр цистерны D = 5 м, длина L = 10 м (рис.
3.14).
Гидрогазодинамика. Метод. указания к самостоятельной работе |
25 |

3. РЕШЕНИЕ ЗАДАЧ
Ответ: РAА = 119·103 кгс; РВВ = 25,5·103 кгс.
2.27. Цилиндрический затвор имеет диаметр D и длину L. Определить величину и направление силы R полного гидростатического давления воды. Уровни воды показаны на рис. 3.16.
Ответ: R = |
3 |
γLD2 |
1+ |
π2 |
; α = arctg |
π . |
|
8 |
|
|
4 |
|
2 |
Рис. 3.16
2.28. Вертикальный цилиндрический резервуар ёмкостью 314 м3 и высотой 4 м заполнен водой. Определить силы давления воды на боковую стенку и дно резервуара.
2.29. В воде плавает бревно объемом V0. Определить погруженную часть его объема V1, если удельный вес дерева γд = 0,8 Т/м3.
Ответ: V1 / V0 = 0,8.
2.30. Найти объем воды Vв, вытесняемый баржей емкостью Vб =10000м3, груженной нефтью удельным весом γ= 0,900 Т/м3.
в= 9000 м3.
2.31.Человек поднимает в обыкновенных условиях железный шар ве-
сом G0 = 30 кг. Какого веса железный шар может быть им поднят под водой? Ответ: G = 34,4 кг.
2.32.Ареометр, изготовленный из полой стеклянной трубки, снабжен
внизу шариком с дробью. Внешний диаметр трубки d = 30 мм; объем шарика V = 15 см3; вес ареометра G = 35,3 г. Определить глубину h, на которую по-
грузится ареометр в спирт удельным весом γ= 700 кгс/м3.
Ответ: h = 5 см.
2.33. Определить, содержится ли примесь породы в самородке золота, если установлено, что вес самородка в воздухе Go = 9,65H, а в воде Gв = 9,15 H. Плотность чистого золота
з= 19,3·103 кг/м3.
2.34.Определить силу, действующую на дере-
вянный брусок длиной L = = 50 см и поперечным сечением S = 200 см2, полностью погруженный в воду. Плотность древесины принять равной ρд = 600 кг/м3.
2.35.Определить давление жидкости в грузовом
гидроаккумуляторе (рис. 3.17), если масса груза равна m1, масса плунжера m2, а его диаметр d. Значения m1,ρ
Рис. 3.17
Гидрогазодинамика. Метод. указания к самостоятельной работе |
26 |

3. РЕШЕНИЕ ЗАДАЧ
m2 и d приведены в табл. 3.6. Трением плунжера в опоре пренебречь.
2.36. Понтон длиной L и массой mn имеет трапецеидальное поперечное сечение, размеры которого указаны на рис. 3.18. Определить максимальную грузоподъёмность mгр понтона, если расстояние ватерлинии от палубы равно b (табл. 3.7). Плотность воды ρ= 1000 кг/м3.
Таблица 3.6
Пара- |
|
|
|
|
Вариант |
|
|
|
|
|
метр |
|
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
m1, кг |
2000 |
2100 |
2200 |
2300 |
2400 |
2500 |
2600 |
2700 |
2800 |
2900 |
m2, кг |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
D, мм |
55 |
60 |
65 |
70 |
75 |
80 |
85 |
90 |
95 |
100 |
Рис. 3.18
Таблица 3.7
Пара- |
|
|
|
|
Вариант |
|
|
|
|
|
метр |
|
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
L, м |
10,0 |
10,5 |
11,0 |
11,5 |
12,0 |
12,5 |
13,0 |
13,5 |
14,0 |
14,5 |
mn, т |
5,0 |
5,4 |
5,8 |
6,2 |
6,6 |
7,0 |
7,4 |
7,8 |
8,2 |
8,8 |
b, м |
0,20 |
0,21 |
0,22 |
0,23 |
0,24 |
0,25 |
0,26 |
0,27 |
0,28 |
0,29 |
Н, м |
4,1 |
4,2 |
4,3 |
4,4 |
4,5 |
4,6 |
4,7 |
4,8 |
4,9 |
5,0 |
h, м |
3,1 |
3,2 |
3,3 |
3,4 |
3,5 |
3,6 |
3,7 |
3,8 |
3,9 |
4,0 |
а, м |
9,0 |
9,2 |
9,4 |
9,6 |
9,8 |
10,0 |
10,2 |
10,4 |
10,6 |
10,8 |
Кинематика несжимаемой жидкости. По теореме Коши-Гельмгольца движение частицы жидкости слагается из поступательного движения центра тяжести частицы со скоростью u0i , из деформационного движения, обуслов-
ленного изменением формы самой частицы со скоростями деформации uiд и из вращательного движения с угловыми скоростями ωi . В общем случае компоненты скорости могут быть представлены в таком виде:
ux = u0x +uxд +(ωy z −ωz y),uy = u0 y +uyд +(ωz x −ωx z),uz = u0z +uzд +(ωx z −ωy x).
При этом
Гидрогазодинамика. Метод. указания к самостоятельной работе |
27 |

3. РЕШЕНИЕ ЗАДАЧ
|
1 |
|
∂u |
|
∂uy |
1 |
∂u |
|
∂u |
|
1 |
∂uy |
|
∂u |
|
|
, |
||
ωx = |
|
|
|
z − |
|
,ωy = |
|
|
x − |
|
z ,ωz = |
|
|
|
− |
|
x |
||
|
|
|
|
|
|
|
|
||||||||||||
|
2 |
|
∂y |
∂z |
|
2 ∂z |
∂x |
2 |
|
∂x |
|
∂y |
|
|
|||||
|
|
|
|
|
|
|
|||||||||||||
или
ω = 0,5rotu .
Характеристиками деформационного движения являются относительные скорости линейной деформации
εx = ∂ux  ∂x,εy = ∂uy
∂x,εy = ∂uy  ∂y,εz = ∂uz
∂y,εz = ∂uz  ∂z
∂z
иотносительные скорости деформации сдвига (угловой деформации)
|
1 |
|
∂u |
|
∂uy |
1 |
∂u |
|
∂u |
|
1 |
∂uy |
|
∂u |
|
|
||
θx = |
|
|
|
z + |
|
,θy = |
|
|
x + |
|
z ,θz = |
|
|
|
+ |
|
x . |
|
|
|
|
|
|
|
|
|
|||||||||||
|
2 |
|
∂y |
∂z |
|
2 ∂z |
∂x |
2 |
|
∂x |
|
∂y |
|
|||||
|
|
|
|
|
|
|||||||||||||
Ускорение жидкой частицы и его проекции на оси декартовых координат в эйлеровых переменных:
ax = ∂∂utx +ux ay = ∂∂uty +ux az = ∂∂utz +ux
∂∂uxx +uy ∂∂uxy +uy ∂∂uxz +uy
∂∂uyx +uz ∂∂uyy +uz ∂∂uyz +uz
∂∂uzx , ∂∂uzy , ∂∂uzz .
Первое слагаемое представляет собой локальное, или местное, ускорение, вызываемое нестационарностью поля скорости, а остальные слагаемые – конвективное ускорение, обусловленное неоднородностью поля скорости.
При движении частиц жидкости различают линию тока, элементарную струйку, вихревую линию и вихревую трубку.
Линией тока называется линия, касательная к каждой точке которой в данный момент времени совпадает с направлением вектора скорости. Линия тока отражает мгновенную картину движения в различных точках. Дифференциальное уравнение семейства линий тока в декартовых координатах:
dx ux =dy
ux =dy uy =dz
uy =dz uz .
uz .
Поверхность, образованная линиями тока, проведенными через все точки бесконечно малого замкнутого контура, называется трубкой тока. Масса жидкости, протекающей внутри трубки тока, называется элементар-
ной струйкой.
Вихревая линия – это линия, касательная во всех точках к векторам уг-
Гидрогазодинамика. Метод. указания к самостоятельной работе |
28 |

3. РЕШЕНИЕ ЗАДАЧ
ловой скорости частиц. Вихревая линия аналогична линии тока. Поверхность, ограниченная вихревыми линиями, проведенными через все точки ка- кого-нибудь бесконечно малого простого замкнутого контура, находящегося в области движущейся жидкости, называется вихревой трубкой. Вихревая трубка аналогична трубке тока. Массу движущейся жидкости внутри вихревой трубки называют вихревым шнуром. Дифференциальное уравнение семейства вихревых линий в декартовых координатах:
dx ωx =dy
ωx =dy ωy =dz
ωy =dz ωz
ωz
Траекторией частицы называется след ее движения в пространстве. Уравнение семейства траекторий получается исключением времени из системы дифференциальных уравнений:
dx dt = ux ,dy
dt = ux ,dy dt = uy ,dz
dt = uy ,dz dt = uz .
dt = uz .
Течение жидкости может существовать лишь в том случае, если оно удовлетворяет уравнению неразрывности, выражающему закон сохранения массы. Уравнение неразрывности для несжимаемой жидкости в декартовых координатах имеет вид
∂ux + ∂uy + ∂uz =0,
∂x ∂y ∂z
или
divu = 0 .
Кинематический анализ потока жидкости с заданным полем скорости включает:
а) проверку удовлетворения уравнению неразрывности; б) определение характеристик движения жидкой частицы (поступа-
тельное, вращательное, деформационное движение); в) нахождение характерных линий течения (линии тока, вихревые ли-
нии, траектории частиц) и их построение.
Кинематический анализ упрощается в частных случаях движения. Плоское течение – течение, одинаковое во всех плоскостях, перпенди-
кулярных некоторой оси (поперечное обтекание цилиндрических тел и т. п.). В случае плоского течения существует функция тока ψ , связанная с проек-
циями скорости зависимостями
ux = ddyψ,uy = − ddxψ .
Гидрогазодинамика. Метод. указания к самостоятельной работе |
29 |

3. РЕШЕНИЕ ЗАДАЧ
Разность значений функции тока в двух точках (А и В) равна расходу жидкости сквозь цилиндрическую поверхность единичной высоты, проходящей через кривую, соединяющую эти точки:
QAB = ψB −ψA .
Знание функции тока упрощает и нахождение линий тока, так как уравнение их семейства принимает вид
ψ = C .
Функция тока по проекциям скорости может быть определена по формуле
yx
ψ= ∫ux (x, y)dy −∫uy (x, y0 )dx ,
y0 |
x0 |
или
yx
ψ= ∫ux (x0 , y)dy −∫uy (x, y)dx .
y0 |
x0 |
Потенциальное движение – вид перемещения, при котором отсутствует вращение частиц и во всех точках которого ω = 0. При этом существует потенциал скорости φ:
x |
y |
z |
ϕ = ∫ux (x, y, z)dx + ∫uy (x, y, z)dy +∫uz (x, y, z)dz , |
||
x0 |
y0 |
z0 |
или
u= gradϕ.
Ввихревых течениях, кроме поступательного движения, происходит вращение частиц жидкости вокруг осей, через них проходящих. Во многих
реальных вихревых течениях ω =/ 0 лишь в небольших областях, имеющих вид вихревых шнуров. Вне этих областей поток можно считать потенциальным. Вихревой шнур малых поперечных размеров по сравнению с потоком можно заменить бесконечно тонкой вихревой нитью с интенсивностью I шнура:
I = ∫rot udS ,
S
Гидрогазодинамика. Метод. указания к самостоятельной работе |
30 |

3. РЕШЕНИЕ ЗАДАЧ
где S – сечение вихревого шнура, нормальное вихревым линиям. По теореме Стокса интенсивность вихря равна циркуляции скорости Г по контуру, охватывающему вихрь. Циркуляция скорости по замкнутому контуру:
Г =  ∫udl =
∫udl = ∫ul dl =
∫ul dl = ∫(uxdx +uydy +uzdz),
∫(uxdx +uydy +uzdz),
l |
l |
l |
где dl (dx, dy, dz) – элемент контура; ul – проекция скорости на касательную
к контуру.
Скорость, вызываемую вихревой нитью в любой точке потока, можно найти по формуле Био-Савара
Г [r dL ], u = 4π ∫L r3
где dL(dx, dy, dz) – элемент нити; r – расстояние от элемента нити до данной
точки потока.
Проекции скорости, индуцированной в точке элементом вихревой нити, равны
dux = 4πГr3 (rzdy − rydz),duy = 4πГr3 (rxdz − rzdx),duz = 4πГr3 (rydx − rxdy).
Если жидкая частица участвует в нескольких движениях, ее скорость равна векторной сумме скоростей составляющих движений:
u∑ =u1 + u2 +....
Пример решения задач
Распределение скорости по сечению плоского канала шириной В при ламинарном установившемся течении вязкой жидкости подчиняется параболическому закону (рис. 3.19):
ux = umax (1− 4y2  В2 ), uy = uz = 0 .
В2 ), uy = uz = 0 .
Рис. 3.19
Гидрогазодинамика. Метод. указания к самостоятельной работе |
31 |

3. РЕШЕНИЕ ЗАДАЧ
Найти характеристики движения жидкой частицы, функцию тока ψ, уравнение семейства линий тока и секундный расход жидкости в канале.
Решение
По характеристикам вращательного и деформационного движения находим:
εx = εy = ax = ay = 0 ,ωz = −0,5∂ux  ∂uy = 4yumax
∂uy = 4yumax  B2 ,
B2 ,
θz = 0,5∂ux  ∂uy = −4yumax
∂uy = −4yumax  B2 .
B2 .
Движение вихревое, сопровождающееся деформацией сдвига, без ускорения. Из уравнения функции тока находим:
ψ = ∫y umax (1− 4y2  B2 )dy = umax (y − 4y3
B2 )dy = umax (y − 4y3  3B2 )+C .
3B2 )+C .
y0
Уравнение семейства линий тока после решения зависимости относительно у превратится в уравнение прямых, параллельных оси х, у = С. Расход в канале:
Q = ψ y=B 2 −ψ y=−B
2 −ψ y=−B 2 = 2(ψ y=B
2 = 2(ψ y=B 2 −ψ y=0 )= 2umax B
2 −ψ y=0 )= 2umax B 3 .
3 .
Задания
3.1. Определить, каким – потенциальным или вихревым – будет движение жидкости, заданное проекциями скоростей u, v, w (табл. 3.8).
Найти функцию потенциала скорости ϕ и составить уравнение линии
тока, если движение потенциальное. Найти составляющие угловой скорости вращения ωx ,ωy ,ωz , если движение вихревое. Примечание: а, в, с – постоян-
ные величины; R = 
 x2 + y2 + z2 .
x2 + y2 + z2 .
|
|
|
|
|
|
|
|
|
Таблица 3.8 |
||
|
|
|
|
|
|
|
|
|
|
|
|
Величина |
|
|
|
|
Вариант |
|
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
u |
-ay |
-2ay |
ву |
2ву |
x+t |
ax/R3 |
bx/R3 |
axy |
bxy |
cxy |
|
v |
ax |
2ax |
-by |
-2bx |
-y+t |
ay/R3 |
by/R3 |
ayz |
byz |
cyz |
|
w |
0 |
0 |
0 |
0 |
0 |
az/R3 |
bz/R3 |
axz |
bxz |
cxz |
|
3.2. Потенциал скорости плоского течения идеальной несжимаемой жидкости задан функцией ϕ=х/(х2+у2).
Найти функцию тока ψ (х, у) для этого течения.
3.3. Комплексный потенциал потока вокруг вихря, расположенного в начале координат:
F(z)= ϕ+iψ = 2Гπi ln z.
Построить линии тока и эквипотенциали. Получить формулу распределения скоростей.
Гидрогазодинамика. Метод. указания к самостоятельной работе |
32 |

3.РЕШЕНИЕ ЗАДАЧ
3.4.Комплексный потенциал диполя (М – момент диполя):
F(z)= ϕ+iψ = M / z.
Построить линии тока и эквипотенциали. Получить формулу распределения скоростей.
3.5. Комплексный потенциал плоского потока идеальной несжимаемой жидкости:
F(z)= ϕ+iψ =1/ z2.
Построить линии тока ψ = const и линии равного потенциала ϕ= const.
3.6. Найти обтекание эллипса (сечение бесконечно длинного эллиптического цилиндра плоскостью) плоскопараллельным потоком идеальной несжимаемой жидкости. Скорость в бесконечности u∞ направлена параллельно
большой оси эллипса. Отношение полуосей эллипса 3:1. Найти максимальную скорость umax . Задачу решить методом комфорного преобразования,
применив к внешней окружности единичного радиуса r0 = 1 преобразование Жуковского:
ζ = z +a2 / z; z = x +iy,
где а – действительная постоянная.
Подсчитать наибольшее pmax и наименьшее pmin давление на поверхности эллиптического цилиндра при u∞ = 60 м/с, давлении в бесконечности p∞ =1·105Па,·плотности жидкости ρ= 1,2 кг/м3.
Динамика невязкой несжимаемой жидкости. Основным объектом изучения гидродинамики является поток жидкости. Различают объемный расход Q, м3/с, и массовый расход G, кг/с, жидкости, которые связаны соотношением
G =ρQ ,
где ρ– плотность жидкости, кг/м3.
Скорость потока определяется как объемный расход вещества через единицу площади сечения потока, F, м2:
u = QF .
При установившемся движении через любое поперечное сечение потока в единицу времени проходит одно и то же количество жидкости (уравне-
ние неразрывности потока):
Q =const
Гидрогазодинамика. Метод. указания к самостоятельной работе |
33 |
3. РЕШЕНИЕ ЗАДАЧ
или
u1 F1 = u2 F2 = K = u F =const .
Основным уравнением гидравлики, определяющим связь между давлением и скоростью в движущемся потоке жидкости, является уравнение Бернулли, все члены которого имеют размерность длины и измеряются высотой столба жидкости:
z1 + |
p |
+ |
u2 |
= z2 + |
p |
+ |
u2 |
, |
|
1 |
1 |
2 |
2 |
||||||
ρ g |
2g |
ρ g |
2g |
||||||
|
|
|
|
|
где z – геометрический напор, высота положения частицы над плоскостью отсчета, м; ρpg – пьезометрический напор, м; z + ρpg – статический напор,
представляющий собой полный запас потенциальной энергии 1 кг жидкости, м;
u2 |
– скоростной напор, представляющий собой удельную кинетическую |
|
2g |
||
|
энергию 1 кг жидкости, м.
Таким образом, при установившемся движении идеальной жидкости для любого сечения справедливо соотношение
z + |
p |
+ |
u2 |
= const . |
|
|
ρ g |
|
2g |
|
|
Физически уравнение Бернулли есть математиче- |
|
||||
ская запись закона сохранения и превращения энергии |
|
||||
применительно к движущейся жидкости. Из уравнения |
|
||||
следует, что если на участке потока уменьшается ско- |
|
||||
рость (кинетическая энергия), то на этом участке долж- |
|
||||
но возрастать давление (потенциальная энергия). |
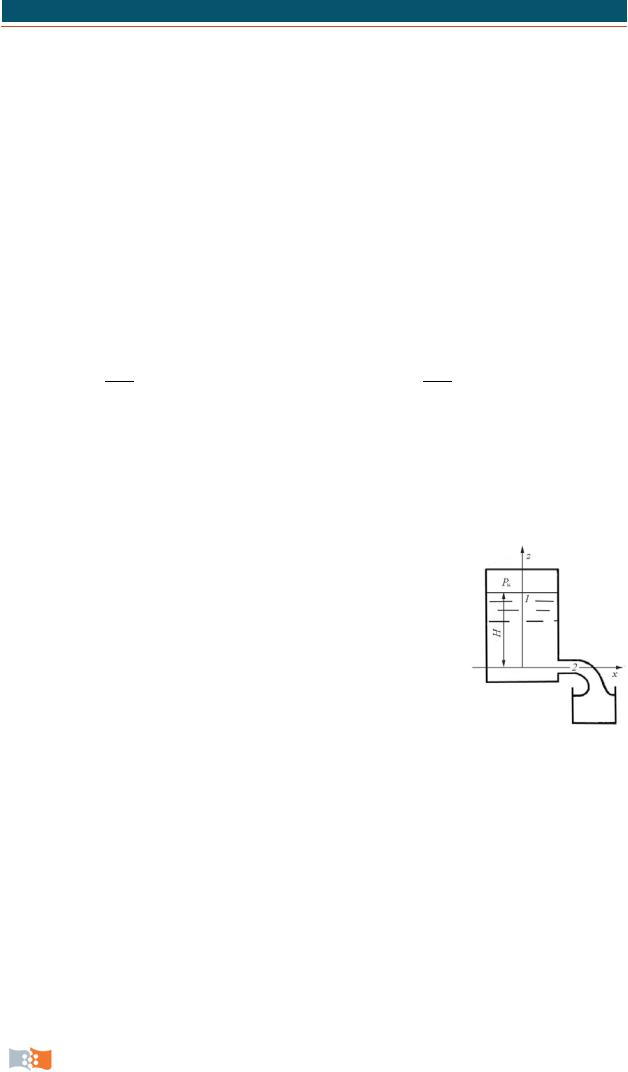
Рис. 3.20 |
||||
|
|
|
|
|
|
Пример решения задач
Считая жидкость невязкой, определить скорость истечения воды из резервуара в атмосферу (рис. 3.20). Уровень воды в баке Н = 5 м и избыточное манометрическое давление ри = 490 гПа постоянны.
Решение
Выберем плоскость сравнения (ось х) по оси выходного сечения и применим интеграл Бернулли к двум точкам одной линии тока: 1 – на поверхности воды и 2 –на выходе струи:
|
p |
|
u2 |
|
p |
|
u2 |
|
|
z1 + |
1 |
+ |
1 |
= z2 + |
2 |
+ |
2 |
. |
|
|
|
||||||||
|
|
||||||||
|
|
||||||||
|
ρ g |
|
2g |
|
ρ g |
|
2g |
|
|
|
|
|
|||||||
Гидрогазодинамика. Метод. указания к самостоятельной работе |
34 |
||||||||

3.РЕШЕНИЕ ЗАДАЧ
Вточке 1 p1 = pa + pи , z1 = H , u1 = 0, так как опускание уровня жидко-
сти в баке, согласно условию задачи, отсутствует. В точке 2 давление р2 равно давлению окружающей среды р2 = ра, а скорость u2 равна искомой скорости истечения u. Подставив найденные значения в уравнение Бернулли, получим
pи |
|
u2 |
|
|
pи |
|
|
|
+ Н = |
, u = 2g |
+ Н . |
||||||
|
||||||||
ρg |
|
2g |
|
|
ρ g |
|
||
|
|
|
|
|||||
Ответ: u = 14 м/с.
Задания
4.1. В шлюзовой камере, имеющей ширину b = 40 м и длину l = 300 м, уровень воды за время τ = 0,5 ч понижается на ∆h = 8 м. Определить сред-
ний расход Q в водоспускных трубах. Ответ: Q = 53,3 м3/с.
4.2. По трубопроводу диаметром d = 156 мм перекачивают мазут удельным весом γ= 0,9 т/м3. Определить объемный расход Q и среднюю ско-
рость u, если весовой расход G = 50 т/ч.
Ответ: Q = 0,0154 м3/с; u = 0,808 м/с.
4.3. Теплообменник изготовлен из стальных труб диаметром 76×3 мм. По трубам проходит газ под атмосферным давлением. Требуется найти необ-
ходимый диаметр при работе с тем же газом, но под давлениемризб= 5 кгс/см2, если требуется скорость газа сохранить прежней при том же массовом расхо-
де газа и том же числе труб.
4.4. Определить (пренебрегая потерями) теоретическое разрежение, которое может быть создано рабочей струей воды в камере А водоструйного насоса (рис. 3.21). Давление на выходе из диффузора атмосферное (1,013·105 Па, или 760 мм рт. ст.), скорость струи в этом месте 2,7 м/с. Диаметр струи в сечении I – 23 мм, в сечении II – 50 мм.
4.5. По горизонтальной трубе переменного сечения протекает идеальная жидкость удельного веса γ =0,95 т/м3 в количестве Q = 10 л/с. Опреде-
лить пьезометрические высоты в сечениях 1, 2, 3, если d1 = d3 = 100 мм, d2 = 25 мм, p1 = 3 атм (рис. 3.22).
Ответ: Pγ1 = Pγ3 = 31,6 м; Pγ2 = 10,48 м.
Гидрогазодинамика. Метод. указания к самостоятельной работе |
35 |

3. РЕШЕНИЕ ЗАДАЧ
Рис. 3.21
Рис. 3.22
4.6. Пожарный, стоя на лестнице, тушит огонь из брандспойта, диаметр которого у устья d = 2 см, а у корня (точка A) D = 8 см. Скорость струи на выходе из брандспойта v = 15 м/с (рис. 3.23). Пренебрегая сопротивлением в стволе, найти силу R, с которой пожарному приходится удерживать брандспойт у точки А.
Ответ: R = 6,75 кгс.
А
Рис. 3.23
4.7. Определить абсолютное давление в диффузоре горизонтальной трубы (рис. 3.24), размеры и расход которых приведены в табл. 3.9. Показания открытого пьезометра h, а плотность жидкости ρ . Потерями напора по
длине трубы пренебречь.
Гидрогазодинамика. Метод. указания к самостоятельной работе |
36 |

3. РЕШЕНИЕ ЗАДАЧ
Рис. 3.24
Таблица 3.9
Параметр |
|
|
|
|
Вариант |
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
d1, мм |
200 |
190 |
180 |
170 |
160 |
150 |
140 |
130 |
120 |
110 |
d2, мм |
0,80 |
0,76 |
0,72 |
0,68 |
0,64 |
0,60 |
0,56 |
0,52 |
0,48 |
0,44 |
Q, м3/c |
36 |
33 |
30 |
27 |
24 |
21 |
18 |
15 |
12 |
9 |
h1, мм |
1,80 |
1,75 |
1,70 |
1,65 |
1,60 |
1,55 |
1,50 |
1,45 |
1,40 |
1,35 |
ρ , кг/м3 |
1000 |
990 |
980 |
970 |
960 |
950 |
940 |
930 |
920 |
910 |
4.8. Вода вытекает из открытого бака большого объема в атмосферу через короткое сопло. Уровень воды в баке над соплом Н = 3 м поддерживается постоянным. Найти массовый расход G воды через сопло, если выходная площадь сопла F = 10 см2.
4.9. Вода вытекает из большого закрытого бака в атмосферу (давление ра = 1·105 Па) через сопло с выходной площадью F = 10 см2. Высота воды в баке над соплом h = 12 м. Над уровнем воды находится воздух давлением p1 = 5·105 Па. Определить скорость истечения воды из сопла.
4.10. Определить массовый расход горячей воды в трубопроводе с внутренним диаметром dвн = 412 мм, если известно, что средняя скорость воды u = 3 м/с, а плотность ρ = 917 кг/м3.
4.11.На прямом участке реки одновременно сделаны замеры попереч-
ного сечения и определены живые сечения в плоскостях А, В, С (рис. 3.25). При этом FА = 50 м2; FВ = 60 м2; FС = 65,5 м2. Расход воды в моме нт определения живых сечений составлял Q = 60 м3/с. Определить средние скорости течения в плоскостях А, В, С.
4.12.По трубопроводу подаётся 0,314 м3/с воды. Определить диаметр трубопровода, если скорость воды равна 2 м/с.
Рис. 3.25
4.13. Пар от двух котлов одинаковой производительности поступает в общий сборный коллектор и далее в турбину (рис. 3.26). Определить диаметр
Гидрогазодинамика. Метод. указания к самостоятельной работе |
37 |

3. РЕШЕНИЕ ЗАДАЧ
паропровода от коллектора к турбине dt, если диаметры паропроводов от коллектора равны d1 = d2 = 150 мм, а скорость пара на всех участках одинаковая.
4.14. По условиям гидравлического испытания водопровода диаметром d = 200 мм и длиной l = 1000 м давление должно быть поднято от атмосферного до 2 МПа. Определить объём воды, который потребуется дополнительно подать в водопровод. Деформацией труб пренебречь.
Динамика вязкой жидкости [1, 5, 13, 14]. Реальные жидкости характеризуются эффектами вязкости (внутреннего трения), что приводит к различию в скоростях по сечению потока: на стенках трубы u = 0 (эффект прилипания), на оси трубы u = umax . Это обстоятельство учитывается введе-
нием поправочного коэффициента α в уравнение Бернулли
(1,0 <α < 2).
Вследствие вязкостных свойств жидкости удельная энергия не может сохраняться неизменной вдоль потока, поэтому в уравнение Бернулли вводят потери энергии на
Рис. 3.26 |
гидравлическое сопротивление hw, м. |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
Тогда для потока реальной жидкости уравнение Бернулли приобретает |
||||||||||
вид |
|
|
|
|
|
|
|
|
|
|
|
|
p |
α u2 |
p |
α |
u2 |
||||
|
z1 + |
1 |
+ |
1 1 |
= z2 + |
2 |
+ |
2 |
2 |
+ hw . |
|
|
|
|
|
|
|||||
|
|
ρ g |
2g |
ρ g |
2g |
|||||
Различают два режима движения жидкости: ламинарный, при котором частицы жидкости движутся, не перемешиваясь, и турбулентный, при котором частицы жидкости движутся неупорядоченно, хаотически. Критерием, определяющим режим движения жидкости, является число Рейнольдса:
Re = udv ,
где u – скорость потока, м/с; d – диаметр трубы, м; v – кинематическая вязкость жидкости, м2/с.
В круглых гладких трубах при Re < 2300 режим движения ламинарный,
при Re > 2300 –турбулентный.
Гидравлические потери hw складываются из потерь энергии на тр ение hλ и потерь на местные сопротивления hм:
hW = hλ + hM .
Линейные потери определяются по формуле Дарси
Гидрогазодинамика. Метод. указания к самостоятельной работе |
38 |

3. РЕШЕНИЕ ЗАДАЧ
hλ = λ l υ2 , d 2g
где l – длина трубы, м; λ – коэффициент сопротивления трения по длине. Для ламинарного движения жидкости коэффициент сопротивления λ
определяется по формуле Пуазейля
λ = Re64 .
При турбулентном движении в трубах с гладкими стенками λ рассчитывается по формуле Блазиуса, если Re = 104–105:
λ = 04,316Re .
При Re > 105 λ определяют по формуле Никурадзе:
λ = 0,0032 + Re0.2210,237 .
Для шероховатых труб, когда 2300 < Re < Renpeд:
k |
э |
|
68 |
0.25 |
||
λ = 0,11 |
|
+ |
Re |
|
, |
|
|
|
|||||
|
d |
|
|
|||
Reпред = 568 d |
, |
|||||
|
|
|
|
k |
|
|
где k – абсолютная шероховатость труб, м.
Для шероховатых труб в квадратичной зоне применяется формула Шифринсона
λ= 0,11 k 0.25 .
d
Коэффициенты сопротивления могут быть найдены по номограммам при из-
вестных значениях Re и относительных шероховатостях труб dk (прил. 3).
Местные сопротивления обусловлены наличием по длине трубопроводов задвижек, вентилей, сужений или расширений труб, поворотов и т. д.
Потери напора hм в местных сопротивлениях определяются по формуле
Гидрогазодинамика. Метод. указания к самостоятельной работе |
39 |

3. РЕШЕНИЕ ЗАДАЧ
hM = ζ υ2 , 2g
где ζ – коэффициент местного сопротивления (приложение 4).
Мощность N, кВт, потребляемая двигателем насоса (вентилятора), рассчитывается по формуле
N =1000Q∆pη ,
где Q – объемный расход жидкости, м3/с; ∆р – повышение давления, сообщаемое насосом перекачиваемому потоку и равное гидравлическому сопротивлению, Па; η – КПД насоса.
∆p = ∆pск + ∆pL + ∆pМ + ∆pпод + ∆pдоп,
где ∆pск – затраты давления на создание скорости потока; ∆pL – потеря давления на трение в трубах; ∆pM – потеря давления на преодоление местных сопротивлений; ∆pпод – затраты давления на подъем жидкости; ∆pдоп – разность давлений в пространстве всасывания (р1)и нагнетания (р2):
∆pск = υ22 ρ,
∆pL = L λ υ2 ρ, d 2
∆pM = ∑ζ υ22 ρ,
где ∑ζ– сумма коэффициентов местных сопротивлений.
∆pпод = ρgh ∆pдоп = p2 − p1 .
Пример решения задач
Определить удельное линейное падение давления в трубопроводе тепловой сети. Внутренний диаметр трубопровода d = 100 мм, температура воды t = 150 °C, скорость u = 2 м/с, абсолютная шероховатость труб k = 0,5 мм.
Решение
Удельное линейное падение давления определяется по формуле
Гидрогазодинамика. Метод. указания к самостоятельной работе |
40 |

3. РЕШЕНИЕ ЗАДАЧ
h = λ 2ud2 ρ.
Для того чтобы выбрать расчетную формулу λ, необходимо определить режим течения воды по критерию Рейнольдса:
Re = udν .
Кинематическая вязкость для воды при t =150 °С ν = 0,202·10-6 м2/с (прил. 5).
Re = |
2 0,1 |
|
=990000 |
, |
|
0,202 10 |
−6 |
||||
|
|
|
Reпред = 568 dk ,
Reпред = 568 5 010,1−4 =113600 .
Так как Re > Renpед, то коэффициент сопротивления трения определяется по формуле Шифринсона
λ= 0,11 k 0,25 = 0,0292 .
d
Плотность воды при t = 150 °С ρв = 917 кг/м3. Удельное линейное падение давления:
h = 0,0292 22 917 =535,5 Па/м. 2 0,1
5.1.Определить режим течения жидкости в межтрубном пространстве теплообменника типа «труба в трубе» при следующих условиях: внутренняя
труба теплообменника имеет диаметр 25 × 2 мм, наружная 51 × 2,5 мм; массовый расход жидкости 3730 кг/ч; плотность жидкости 1150 кг/м3; динамический коэффициент вязкости 1,2·10-3 Па·с.
5.2.В резервуар подаётся постоянный поток жидкости объемом Q. Определить путевые потери давления на трение жидкости вязкостью νæ , трубо-
провода диаметром d и длиной l (табл. 3.10). В качестве жидкости выбрать масло марки М-10-В2 (прил. 4).
Гидрогазодинамика. Метод. указания к самостоятельной работе |
41 |

3. РЕШЕНИЕ ЗАДАЧ
Таблица 3.10
Параметр |
|
|
|
|
Вариант |
|
|
|
|
||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
||
|
|||||||||||
Q, л/мин |
10 |
12 |
14 |
16 |
18 |
20 |
22 |
24 |
26 |
28 |
|
d, мм |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
|
l, м |
4,0 |
4,2 |
4,4 |
4,6 |
4,8 |
5,0 |
5,2 |
5,4 |
5,6 |
5,8 |
|
νæ ·10–6, м2/с |
300 |
330 |
360 |
390 |
420 |
450 |
480 |
510 |
540 |
570 |
|
5.3.Определить характер движения нефти по нефтепроводу диаметром d = 305 мм, если ее расход Q = 60 л/с, а вязкость 0,082 см2/с.
Ответ: Re = 2290 (переходная зона).
5.4.Нефть удельным весом γ = 8,5·103 Н/м3 и вязкостью µ =0,03
кгс·с/м2 перекачивается по трубопроводу диаметром d = 203 мм. Определить весовой расход G, при котором движение переходит из ламинарного в турбулентное.
Ответ: G = 107 кг/с.
5.5.Определить наибольшую величину диаметра трубы d, при котором на достаточном удалении от входа будет иметь место ламинарное течение,
если через поперечное сечение трубы протекает Q = 2 л/с керосина кинематической вязкостью νкр = 0,05 см2/с. Найти также, какова будет при этом средняя скорость течения керосина u.
Ответ: d = 219,5 мм; u = 5,28 м/с.
5.6.По трубопроводу диаметром d = 203 мм перекачивается Q = 100 л/с мазута, кинематическая вязкость которого ν постепенно увеличивается
вследствие остывания. Определить, при каком значении вязкости νкр в трубе будет иметь место критический режим движения.
Ответ: νкр = 2,7 см2/с.
5.7. Определить режим движения воды при состоянии насыщения по трубопроводу, имеющему внутренний диаметр 125 мм, при объёмном расходе Q = 88,2 м3/ч. Температура воды 150 ºС. Физические характеристики воды
даны в прил. 5. |
|
5.8. Определить удельное линейное па- |
|
дение давления в трубопроводе тепловой се- |
|
ти. Внутренний диаметр трубопровода d = |
|
100 мм, температура воды t = 150 °C, скорость |
|
u = 0,2 м/с, абсолютная шероховатость труб |
|
k = 0,5 мм. Физические характеристики воды |
|
даны в прил. 5. |
|
5.9. Определить предельное значение |
|
скорости воды в трубопроводах тепловой се- |
|
ти, выше которой линейное падение давле- |
|
ния (потери напора) прямо пропорционально |
|
квадрату скорости. Температура воды t = |
Рис. 3.27 |
150°C, абсолютная шероховатость труб k = 0,5 мм. Физические характери-
Гидрогазодинамика. Метод. указания к самостоятельной работе |
42 |

3. РЕШЕНИЕ ЗАДАЧ
стики воды даны в прил. 5.
5.10. Жидкость, имеющая плотность 1200 кг/м3 и динамический коэффициент вязкости 2 мПа·с, из бака 1 с постоянным уровнем самотёком поступает в реактор 2. Определить, какое максимальное количество жидкости (при полностью открытом кране) может поступать из бака в реактор. Уровень жидкости в баке находится на 6 м выше ввода жидкости в реактор. Трубопровод выполнен из алюминиевых труб с внутренним диаметром 50 мм. Общая длина трубопровода, включая местные сопротивления, 16,4 м. На трубопроводе имеются три колена и кран (рис. 3.27). В баке и реакторе давление
атмосферное.
Ответ: 20,5 м3/ч.
5.11. Трубопровод диаметром d = 100 мм имеет местное сужение, в котором его диаметр d1 = 25 мм. Определить весовой расход G, среднюю скорость в трубопроводе u и скорость в узкой е го части u1, если перекачивается
мазут удельным весом γ = 900 кгс/м3 в количестве Q = 10 л/с.
Ответ: G = 9,5 кг/с; u = 1,27 м/с; u1 = 20,4 м/с.
5.12. Определить гидравлический уклон i в трубопроводе постоянного диаметра длиною l = 10 км при перекачке воды, если в начале трубы давление p1 больше, чем давление в конце р2, на величину ∆р = 30 атм, и конец трубы расположен выше начала на ∆z = 20 м.
Ответ: i = 0,028 м.
5.13. По нефтепроводу перекачивается нефть удельным весом γ = 900
кгс/см3 в количестве Q = 40 л/с. В одном сечении внутренний диаметр трубы d1 = 305 мм и давление р1 = 10 атм, в другом сечении, расположенном выше первого на ∆z = 10 м, внутренний диаметр трубы d2 = 254 мм и давление р2 = 8 атм. Определить высоту потерянного напора hr между этими сечениями.
Ответ: hr = 12,48 м.
5.14. Пожарный рукав диаметром d = 75 мм имеет на своем конце коническую насадку (брандспойт). Потеря напора при прохождении воды через нее равна h = 0,5 м; расход воды Q = 7 л/с. Найти, какое давление должна иметь вода перед входом в брандспойт, для того чтобы струя из него била на высоту Н = 15 м.
|
|
|
5.15. На заданном профиле местности про- |
|
|
|
|
||
b |
||||
ложен трубопровод и установлена насосная стан- |
||||
|
|
|
||
|
|
С |
ция (пункт а). Напор, развиваемый насосами, изо- |
|
|
|
бражается отрезком ab, а падение напора при пе- |
||
a |
рекачке – наклонной прямой bс (рис. 3.28). Опре- |
|||
|
|
|
делить, в каком месте трубопровода будет наи- |
|
|
|
|
высшее давление и как его найти. Удельный вес |
|
|
|
|
||
|
Рис. 3.28 |
жидкости считается известным. |
||
5.16. Поток воды у входа в турбину (рис 3.29) в сечении I–I имеет среднюю скорость u1 = 1,8 м/с и давление p1 = 2 атм, а на выходе из турбины (сечение
Гидрогазодинамика. Метод. указания к самостоятельной работе |
43 |

3. РЕШЕНИЕ ЗАДАЧ
II–II) u2 = 1,2 м/с и р2 = 0,3 атм. Расстояние между сечениями I-I и II-II, изме-
ренное по высоте, ∆z = 3 м. Расход воды, проходящей через турбину, Q = 72000 м3/ч.
|
v1 |
I |
I |
II |
II |
|
v2 |
|
Рис. 3.29 |
Определить мощность N на валу турбины, если ее КПД η = 0,6. Ответ: N = 4310 л.с.
5.17.По прямой трубе длиною l = l км, диаметром d = 100 мм протекает
со средней скоростью u = 0,4 м/с жидкость, имеющая кинематическую вязкость ν = 0,4 см2/с. Определить потерю напора на трение h.
Ответ: h = 5,2 м.
5.18.Определить суточную пропускную способность самотечного нефтепровода диаметром d = 203 мм при движении по нему нефти удельным ве-
сом γ = 900 кгс/м3, вязкостью ν = l,46 см2/с. Длина трубопровода l = 10 км, и
начальная точка лежит выше конечной на ∆z = 50 м. Ответ: G = 1090 т/с.
5.19. Электростанция потребляет в сутки G = 2200 т мазута. Мазут имеет вязкость 0,313 см2/с и удельный вес γ= 925 кгс/м3 и перекачивается с неф-
тесклада по горизонтальному трубопроводу диаметром d = 203 мм, длиной l = l км. Определить абсолютное давление р, развиваемое насосами, если давление в конце трубопровода должно быть равно р2 = 1,5 атм.
Ответ: р1 = 11,5 атм.
5.20. Определить потерю напора h в трубопроводе диаметром
d = 257мм, длиной l = 1000 м при kэкв = 0,15 мм, если весовой расход нефти, перекачиваемой по этому трубопроводу, G = 200 т/ч, удельный вес нефти
γ = 880 кгс/м3 и вязкость ν = 0,276 см2/с. Обосновать также выбор расчетной
формулы.
Ответ: h = 9 м.
5.21.По горизонтальному трубопроводу длиной l = 40 км и диаметром
d = 203 мм (kэкв = 0,15 мм) перекачивается вода при температуре t = 20 °С в количестве Q = 90 м3/ч. Обосновать выбор расчетной формулы и определить перепад давления ∆р.
Ответ: ∆р = 12,1 атм.
5.22.Определить потерю напора h во всасывающей трубе центробеж-
Гидрогазодинамика. Метод. указания к самостоятельной работе |
44 |

3. РЕШЕНИЕ ЗАДАЧ
ного насоса длиною l = 20 м, диаметром d = 200 мм при расходе Q = 60 л/с. На трубе имеется три закругления (ζзак = 0,2) и один всасывающий клапан
(ζкл = = 5); коэффициент гидравлического сопротивления λ = 0,022.
Ответ: h = 1,45м.
5.23. Труба имеет внезапное расширение от диаметра d1 = 100 мм до диаметра d2 = 300 мм. Определить потерю напора hм и коэффициент местного сопротивления ζ2 , отнесенный к скорости в широком сечении, если объем-
ный расход Q = 35,3 л/с.
Ответ: ζ2 = 64; hм = 0,816 м.
5.24. В сосуд, имеющий отверстие в дне (µ и ν считаются заданными),
вначале пустой, непрерывно подается некоторое количество жидкости Q. Определить, возможно ли при каких-либо условиях полное опорожнение сосуда и какова должна быть высота сосуда Н для того, чтобы он не переполнялся.
Ответ: Нет,H = |
Q2 |
. |
|
µ2υ2 2g |
|||
|
|
5.25. Имеется затопленный прямоугольный водослив с острым ребром (или с тонкой стенкой). Ширина порога водослива b = 15 м, высота водослива р = 1,2 м, напор над гребнем водослива Н = 2 м, глубина подтопа hn = l,2 м. Определить расход воды Q (рис. 3.30).
H |
Z |
|
hn |
||
|
||
P |
|
Рис. 3.30
Ответ: Q=86,2 м3/с.
5.26. Через незатопленный водослив в тонкой стенке с порогом прямоугольного профиля необходимо пропустить воду в количестве Q = 20 м3/с. Ширина водослива b = 2 м. Определить, на какую высоту поднимается вода перед водосливом против его кромки, если ширина потока перед водосливом В = 8 м, высота порога над дном верхнего бьефа рв = 0,8 м, скорость подхода воды к гребню водослива u0 = 2 м/с (рис.3.31).
Ответ: Н = 2,985 м.
Гидрогазодинамика. Метод. указания к самостоятельной работе |
45 |
3. РЕШЕНИЕ ЗАДАЧ
b
B
В 



h
Рис. 3.31
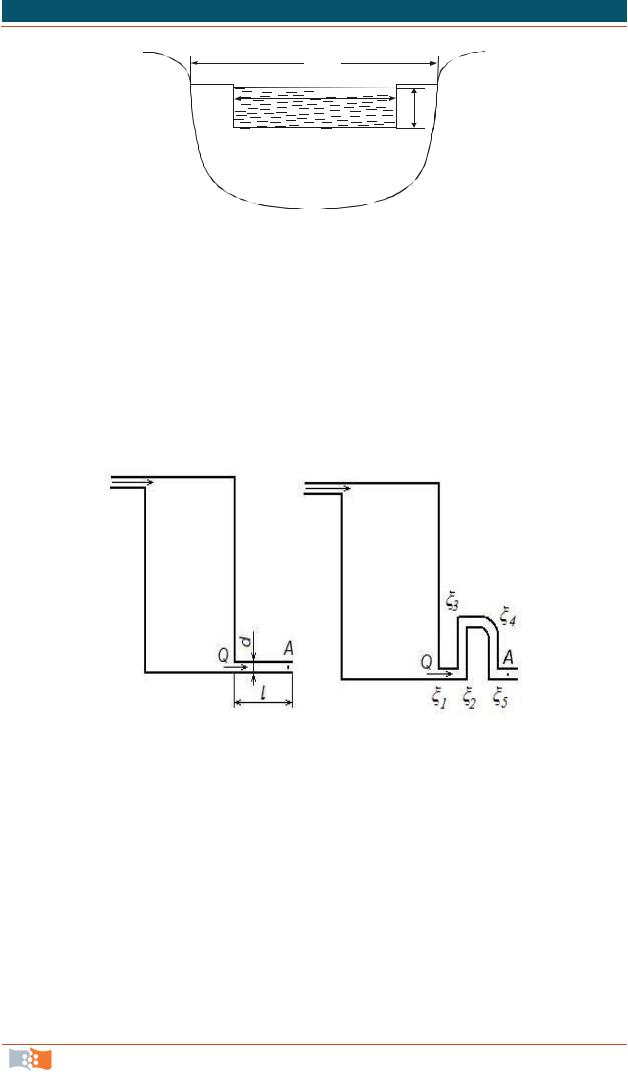
5.27. В резервуар подается постоянный поток жидкости Q (рис. 3.32). Определить путевые потери на трение жидкости вязкостью νж в точке А тру-
бопровода диаметром d и длиной l. Значения параметров указаны в табл.
3.11. Марка жидкости М-10-В2.
5.28. В резервуар подаётся постоянный поток жидкости Q (рис. 3.33). Определить местные потери давления жидкости вязкостью νж в коротком
трубопроводе. Суммарный коэффициент местных сопротивлений ζ =ζ1 +ζ2 +ζ3 +ζ4 +ζ5 приведён в табл. 3.12. Свойства жидкости МГ-15-В(с) в прил. 2.
|
|
Рис. 3.32 |
|
|
Рис. 3.33 |
|
|
|
||
|
|
|
|
|
|
|
|
|
Таблица 3.11 |
|
|
|
|
|
|
|
|
|
|
|
|
Параметр |
|
|
|
|
Вариант |
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
Q, л/мин |
10 |
12 |
14 |
16 |
18 |
20 |
22 |
24 |
26 |
28 |
d, мм |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
l, м |
4,0 |
4,2 |
4,4 |
4,6 |
4,8 |
5,0 |
5,2 |
5,4 |
5,6 |
5,8 |
νж ·10-6, м2/с |
300 |
330 |
360 |
390 |
420 |
450 |
480 |
510 |
540 |
570 |
Гидрогазодинамика. Метод. указания к самостоятельной работе |
46 |

3. РЕШЕНИЕ ЗАДАЧ
Таблица 3.12
Параметр |
|
|
|
|
Вариант |
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
Q, л/мин |
30 |
28 |
26 |
24 |
22 |
20 |
18 |
16 |
14 |
12 |
d, мм |
15 |
14 |
13 |
12 |
11 |
10 |
9 |
8 |
7 |
6 |
ζ |
4 |
5 |
7 |
6 |
4 |
5 |
7 |
6 |
4 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
νж ·10-6, м2/с |
510 |
480 |
450 |
420 |
390 |
360 |
330 |
300 |
270 |
240 |
5.29. Определить скорость истечения и расход воды из бака через круглое отверстие d = 10 см, если превышение уровня воды над центром отверстий Н = 5 м. Коэффициент расхода µ= 0,62.
5.30. Определить теоретический расход воды, если разность напоров в большом и малых сечениях водомера Вентури ∆h = 500 мм рт. ст. Диаметр трубопровода D = 300 мм, диаметр цилиндрического участка водомера d = 100 мм.
5.31. Определить расход воды, вытекающей из бассейна: а) через отверстие в стенке; б) через внутренний цилиндрический насадок;
в) через внешний цилиндрический насадок; г) через коноидальный насадок.
Внутренний диаметр выходных отверстий d = 100 мм. Высота уровня воды над центром отверстия 5 м.
5.32. Для целей горячего водоснабжения к потребителям подаётся вода в количестве Q = 200 м3/ч при температуре t = 70 °C. Длина трубопровода l = 1000 м, внутренний диаметр dв = 259 мм, давление воды в начале линии p1 = 5 кгс/см2. Отметка оси трубопровода в конечной точке на 2 м выше начальной. Определить полный напор и давление в начале и конце трубопровода, если шероховатость труб k = 5·10-4 м, а потеря напора в местных сопротивлениях равна 10 % линейных потерь.
5.33. Определить скорость газов в газоходе парового котла, если динамический напор, измеренный с помощью спиртового манометра, равен
hcп = 4 мм, средняя температура газов в газоходе tг = 367 °C. Плотность газов при нормальных физических условиях ρг = 1,29 кг/м3; плотность спирта
ρс = 0,8·103 кг/м3; ϕ = 0,98.
5.34. Определить потерю напора в прямом трубопроводе длиной l=1000м,по которому прокачивается нефтепродуктплотностью ρ= 900 кг/м3 в
количестве Q = 31,4 л/с. Внутренний диаметр трубопровода d = 200 мм, коэффициент гидравлического сопротивления λ= 0,04.
5.35. Определить возможный расход из водопровода в здании, расположенном на расстоянии 1 км от водонапорной башни, если известно, что уровень воды в башне поддерживается постоянным на высоте 20 м. Вода в здание должна быть подана на высоту 10 м. Водопровод имеет внутренний диаметр d = 175 мм и проложен по прямой между водонапорной башней и
Гидрогазодинамика. Метод. указания к самостоятельной работе |
47 |

3. РЕШЕНИЕ ЗАДАЧ
зданием.
5.36.Определить необходимую высоту уровня воды в напорном баке,
предназначенном для подачи воды потребителям по трубопроводу диаметром d = 125 мм и длиной l = 1200 м, если расход Q = 60 м3/ч.
5.37.Определить диаметр трубы, через которую необходимо подать 180 м3/чводынарасстояние300 м,если уровеньводы внапорномбакена15 м выше места водозабора.
5.38.Турбинное масло течет по длинной круглой гладкой горизонтальной трубе диаметром d = 25 мм. Массовый расход Q = 0,35 кг/с. Определить
падение давления, отнесенное к единице длины трубы, ∆p /l . Физические свойства турбинного масла приведены в прил. 2. Температура масла
Т= 239 К.
5.39.Вода течет по длинной круглой гладкой горизонтальной трубе диаметром d = 200 мм. Определить падение давления, отнесенное к единице
длины трубы, ∆p /l при массовом расходе Q = 150 кг/с и температуре воды
Т= 313 К. Какой будет величина ∆p /l при уменьшении расхода в 2 раза.
5.40.30 т/ч нитробензола при 20 °С перекачиваются насосом из бака с
атмосферным давлением в реактор, где поддерживается избыточное давление 0,1 кгс/см2, т.е. ~ 0,01 Мпа. Трубопровод выполнен из стальных труб диаметром 89×4 мм с незначительной коррозией. Длина всего трубопровода, включая местные сопротивления, 45 м. На трубопроводе установлены: диафрагма
(do = 51.3 мм), две задвижки и четыре отвода под углом 90 º с радиусом изгиба 160 мм. Высота подъёма жидкости 15 м. Найти мощность, потребляемую насосом, приняв общий КПД его равным 0,65.
5.41.Минеральное масло в количестве 40 м3/ч перекачивается по трубопроводу диаметром 108×4 мм в бак, помещённый на высоте 20 м. Длина горизонтального участка трубопровода 430 м. Вычислить необходимую мощность насоса, если перекачка осуществляется: а) при 15 °С и б) при 50 °С. При этих температурах плотность масла составляет 960 и 890, динамический коэффициент вязкости 3,43 и 0,187 Па·с, соответственно. Экономично ли подогревать до 50 °С масло перед перекачкой, если 1 кВт·ч электроэнер-
гии стоит 4 коп., а 1 т греющего (отбросного) пара (рабс = 1 кгс/см2, т. е.
~0,1 Мпа) 2 руб. и если общий КПД насосной установки равен 0,5.
5.42.При тепловом расчете теплообменника для нагрева некоторого раствора был выбран по каталогу четырёхходовой кожухотрубчатый теплообменник, в котором раствор проходит по трубному пространству со скоростью 0,3 м/с. Определить гидравлическое сопротивление трубного пространства. Характеристика теплообменника: общее число труб 90, трубы стальные диаметром 38×2 мм с незначительной коррозией, высота трубного пространства 2 м, штуцеры для раствора имеют диаметр 159×4,5 мм. Средняя темпе-
ратура раствора 47,5 °С, динамический коэффициент вязкости 0,83 мПа·с, плотность 1100 кг/м3.
5.43. Определить суммарные потери давления в трубопроводе (рис. 3.34) диаметром 20 мм на участке между точками А и В, если скорость
Гидрогазодинамика. Метод. указания к самостоятельной работе |
48 |

3. РЕШЕНИЕ ЗАДАЧ
потока жидкости u, суммарный коэффициент местных сопротивлений ζ = ζ1 + ζ2 + ζ3 + ζ4 , а общая протяжённость прямолинейных участков трубо-
провода l=l1+l2+l3+l4 (табл. 3.13). Плотность жидкости M-8-B2 дана в прил. 2.
Рис. 3.34
Таблица 3.13
Параметр |
|
|
|
|
Вариант |
|
|
|
|
||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
||
|
|||||||||||
u, м/с |
4,0 |
' 4,3 |
4,6 |
4,9s |
5,2 |
5,5 |
5,8 |
5,1 |
5,4 |
5,7 |
|
ζ |
2,5 |
2,8 |
зд |
3,4 |
3,7 |
4,0 |
4,3 |
4,6 |
4,9 |
5,2 |
|
l,м |
10,0 |
9,5 |
9,0 |
8,5 |
8,0 |
7,5 |
7,0 |
6,5 |
6,0 |
5,5 |
|
νж ·10-6, м2/с |
600 |
570 |
540 |
510 |
480 |
450 |
420 |
390 |
360 |
330 |
|
5.44. Вода (Q = 35·103 кг/ч) течет по трубе диаметром d1 = 50 мм, соединенной без перехода с трубой диаметром d2 = 80 мм. Определить потери давления р2 – р2 вследствие внезапного изменения диаметра трубы. Рассчитать коэффициент потерь ζ , т. е. отношение потерь давления к кинетической
энергии потока.
Газовая динамика [1, 5, 13, 14]. Вопросы движения в потоке газа с большими скоростями рассматриваются в рамках газовой динамики.
Скорость, с которой в массе газа распространяются возмущения давления, зависит от термодинамического состояния газа и играет важную роль для выяснения особенностей движения газа.
Параметры торможения – это значение энтальпии, температуры, давления и плотности в той точке, где скорость потока равна нулю, т. е. поток полностью заторможен. В результате полного торможения вся кинетическая энергия направленного движения переходит во внутреннюю энергию. При полном торможении потока совершенного газа температура торможения То, как и энтальпия, может иметь только одно определённое значение, в то время как давление торможения р0 и плотность ρ0 могут принимать любые значе-
ния, но такие, при которых отношение р0
ρ0
остаётся постоянным. Следует
уяснить, что при определении параметров торможения не имеется в виду реальное торможение потока. Параметры торможения формально вычисляются в данном сечении потока по соответствующим уравнениям и имеют большое значение при рассмотрении как теоретических, так и экспериментальных за-
Гидрогазодинамика. Метод. указания к самостоятельной работе |
49 |

3. РЕШЕНИЕ ЗАДАЧ
дач газовой динамики. Параметры изоэнтропийного торможения определяются из уравнения энергии при постоянной теплоёмкости:
СpT +1 2u2 =СpT0 ,
2u2 =СpT0 ,
где Сp – теплоёмкость газа при постоянном давлении; Т – температура газа в произвольном сечении сопла, К; u – скорость газа в произвольном сечении сопла, м/с; Т0 – температура торможения газа, К.
Тогда температура торможения:
T0 =T + 0,5u2 /Cp .
Давление и плотность заторможенного газа находятся из уравнения изоэнтропы:
p p0 = (ρ/ ρ0 )k ,
p0 = (ρ/ ρ0 )k ,
где р и ρ – давление, Па, и плотность газа, кг/м3, в произвольном сечении сопла, соответственно; k – показатель изоэнтропы:
k = Cp  Cv ,
Cv ,
ρ ρ0 = (T /T0 )1/(k −1) ,
ρ0 = (T /T0 )1/(k −1) ,
ρ = p RT ,
RT ,
где R – газовая постоянная, для воздуха R = 287Дж/(кг·К):
R =Cp −Cv ,
p p0 = (T /T0 )k /(k−1) .
p0 = (T /T0 )k /(k−1) .
Температуру, давление и плотность заторможенного газа можно определить по таблицам газодинамических функций − безразмерных параметров, позволяющих упрощать анализ уравнений газовой динамики, а также расчётприл( . 6, 7).
Температуру, давление и плотность удобно измерять в долях от их значений в заторможенном потоке:
τ =T T0 ; ε = p
T0 ; ε = p p0 ; δ =ρ
p0 ; δ =ρ ρ0 .
ρ0 .
Сначала определяют число Маха – отношение скорости потока к местной скорости звука:
Гидрогазодинамика. Метод. указания к самостоятельной работе |
50 |

3. РЕШЕНИЕ ЗАДАЧ
M =u a .
a .
Для идеального газа скорость распространения звука зависит только от его температуры:
a = 
 k R T ,
k R T ,
тогда
M= u

 k R T .
k R T .
Спомощью линейной интерполяции находят τ, ε, δ , соответствующие полученному значению М, а затем определяют Т0, p0, ρ0 .
Пример решения задач
Воздух течет по трубе, площадь поперечного сечения которой меняется по длине. В некотором сечении площадью F1 число M1 = 0,6, в другом сечении площадью F2 M2 = 0,85. Определить отношение площадей F2 / F1 при условии, что течение можно рассматривать как одномерное изоэнтропийное.
Какое отношение скоростейu2 / u1 и температурT2 /T1 потока в этих сечениях?
Решение
С помощью функции
q = F  F
F
для двух различных сечений в трубе получим соотношение ( F = const в изоэнтропийном потоке)
F2  F1 = q1
F1 = q1  q2 ,
q2 ,
где q1, и q2 найдены по таблицам газодинамических функций (прил. 6) при
M1 = 0,6 и M2 = 0,85:
F2  F1 = 0,8415
F1 = 0,8415 0,9797 = 0,8589 .
0,9797 = 0,8589 .
По таблицам газодинамических функций (прил. 6) получены значения
λ1 = 0,4030; λ2 = 0,7686: τ1, = = 0,9328; τ2, = 0,8737.
Отношение скоростей
u2  u1 =(u2
u1 =(u2  a )
a ) (u1
(u1  a )= λ2
a )= λ2  λ1 ,
λ1 ,
где a – const.
u2  u1 =0,7686
u1 =0,7686 0,4030 =1,907 .
0,4030 =1,907 .
Гидрогазодинамика. Метод. указания к самостоятельной работе |
51 |

3. РЕШЕНИЕ ЗАДАЧ
Отношение температур:
T2  T1 = (T2
T1 = (T2  T0 )
T0 ) (T1
(T1  T0 )=τ2
T0 )=τ2  τ1 .
τ1 .
T2  T1 =0,8737
T1 =0,8737 0,9328 = 0,9366 .
0,9328 = 0,9366 .
Задания
6.1. Определить число М, скорость звука и параметры торможения (p0, R0, ρ0) газового потока, перемещающегося в условиях энергетической изоляции (изоэнтропических условиях) со скоростью u при давлении p, если известен показатель адиабаты k, газовая постоянная R и максимальная скорость
uмах (табл. 3.14). Построить графики зависимостей u(M) и a(М) при условии
изменения скорости от u = 0 до uмах.
6.2. Невозмущённый газовый поток, движущийся со скоростью u1, находился под давлением р1 , температура t1 (табл. 3.15).Определить скорость ,
статическое и полное давление за прямым скачком уплотнения, если извест-
но, что R = 420 Дж/кг·К, k = 1,4 и сp = 1470 Дж/кг·К.
6.3. Тело движется в стратосфере на высоте 20 км со скоростью u = 1000 км/ч. Определить значение критерия Маха и коэффициент скорости λ, если давление воздуха р = 54,4 миллибара, а удельный вес γ = 0,09 кгс/м3.
Ответ. М = 0,965; λ = 1,065.
Таблица 3.14
Величина |
|
|
|
|
Вариант |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
k |
1,4 |
1,4 |
1,4 |
1,4 |
1,33 |
1,33 |
1,33 |
1,33 |
1,4 |
1,4 |
R, Дж/кг·К |
31 |
31 |
300 |
300 |
286 |
286 |
273 |
273 |
309 |
309 |
u, м/с |
350 |
400 |
522 |
500 |
305 |
550 |
305 |
600 |
720 |
650 |
p, кПа |
120 |
130 |
8607 |
110 |
96 |
100 |
110 |
80 |
50 |
60 |
umах , м/c |
715 |
841 |
830 |
916 |
1115 |
1052 |
985 |
1162 |
1080 |
1114 |
|
|
|
|
|
|
|
|
|
|
|
Таблица 3.15
Величина |
|
|
|
|
Вариант |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
||
|
|||||||||||
u1, м/с |
500 |
550 |
600 |
650 |
700 |
750 |
800 |
750 |
700 |
650 |
|
p1, бар |
2,2 |
2,0 |
1,8 |
1,6 |
1,4 |
1,2 |
1,0 |
1,1 |
1,2 |
1,3 |
|
t1, °С |
20 |
23 |
25 |
27 |
30 |
33 |
35 |
40 |
35 |
30 |
|
6.4. Газ метан при давлениир= 10 атм имеет удельный вес γ = 6,29 кгс/м3.
Скорость течения газа u = 80 м/с. Определить температуру, которую покажет термометр, поставленный в потоке газа. Теплоёмкость метана принять ср = 0,53 ккал/кг°С .
Гидрогазодинамика. Метод. указания к самостоятельной работе |
52 |

3. РЕШЕНИЕ ЗАДАЧ
Ответ. Т = 301,45 К.
6.5. Поток воздуха при давлении р = 10 атм и температуре t = −8 °С течёт со скоростью u = 100 м/с. Определить температуру Т0, давление р0 и плотность ρ0 этого потока при адиабатическом торможении до состояния по-
коя, а также найти скорость звука а в потоке.
Ответ. Т0 = 270 °К; р0 = 10,68 атм; ρ0 = 1,37 кгс·с2/м4; а = 330 м/с.
6.6. Газ с параметрами торможения р0 = 10·155Па и Т0 = 1500 К вытекает из камеры через сопло Лаваля с площадью минимального сечения Fmin = 100 см2 и выходного сечения F1 = 400 см2. Давление в пространстве за соплом равно расчетному. Найти реактивную силу L. Газовая постоянная R = 280 Дж/(кгК), показатель изоэнтропы k = 1,35, трением пренебречь.
6.7.Расширяющееся сопло Лаваля предназначено для разгона потока до сверхзвуковой скорости. Какая скорость воздуха в выходном сечении сопла будет получена в расчетном режиме работы, если отношение площади
минимального сечения к выходному F1/Fmin = 2. Чему равна температура воздуха Т в струе, выходящей из сопла. Температура торможения Т0 = 700 К, k = 1,4, течение изоэнтропийное.
6.8.Изоэнтропийный одномерный поток воздуха течет по трубе пере-
менного сечения. В двух сравниваемых сечениях известны числа М1 = 0,7 и М2 = 1,4. Найти отношения скоростей u2 /u1 и температур Т2 / Т1 воздуха в этих
сечениях. Задачу решить как по формулам, так и с помощью таблиц газодинамических функций (прил. 6, 7).
6.9. Изменение площади поперечного сечения трубы F задано уравне-
нием F/Fmin = 2 –e−x2 . Течение воздуха в трубе рассматриваем как одномерное изоэнтропийное. Можно ли в каком-либо сечении трубы произвольно задать число Маха М. Если нет, то определить границы возможных чисел М, н а- пример, для сечения х = –1.
6.10. Изменение площади поперечного сечения трубы задано уравнени-
ем F/Fmin = 2 –e−x2 . Течение одномерное изоэнтропийное. Построить графики распределения вдоль трубы чисел М = u/а, безразмерного давления ε = р/р0, безразмерной температуры τ = Т/Т0 (индексом 0 отмечены параметры торможения). Расчеты провести для двух случаев: 1) при х = –1 известно число Маха М1 = 0,25; 2) известно, что в трубе дозвуковое течение переходит к сверхзвуковому. Расчеты провести по пяти точкам в пределах –1≤ х ≤1.
6.11.Воздух движется по трубе переменного сечения. Течение одномерное изоэнтропийное. Отношение минимальных площадей поперечных сечений
трубы F1 / F2 = 2. Какие минимальные и максимальные отношения скоростей u2 / u1 потока в этих сечениях, если скорость в сеченииF1 дозвуковая.
6.12.Воздух выходит через суживающееся сопло с площадью выходного сечения F = 20·10-3 м2 и Т0 = 500 К, давление за соплом p1 = 6·105 Па. Определить расход воздуха. Задачу решить по формуле и с помощью таблиц газодинамических функций. Течение одномерное изоэнтропийное.
6.13.Воздух движется со скоростью u = 200 м/с, статическое давление
ρ= 0,5·105 Па, статическая температура Т = 300 К. Найти параметры изоэн-
Гидрогазодинамика. Метод. указания к самостоятельной работе |
53 |

3. РЕШЕНИЕ ЗАДАЧ
тропийного торможения (давление р0, температуру Т0, плотность ρ0). 3адачу решить по формулам и с помощью таблиц газодинамических функций.
6.14.Поток перегретого водяного пара движется со скоростьюu=250м/с, статическое давление р1 = 1,5·105 Па, статическая температура Т1 = = 573 К. Определить параметры изоэнтропийного торможения (энтальпию h0, давление р0 и температуру t0). Задачу решить по формулам, считая, что пар при этих параметрах подчиняется законам совершенного газа с показателем изоэнтропы k = 1,3 и R = 461,5 Дж/(кг·К).
6.15.Самолёт летит со скоростью u = 2500 км/ч. Температура окружающего воздуха Т = 233 К, давление р = 36·103 Па. Какую максимальную
температуру Тmax могла иметь наружная поверхность обшивки самолёта при отсутствии теплопередачи. Какое давление p0 может быть получено насадком полного давления, установленного на самолёте.
6.16.Скорость воздуха u = 600 м/с, а температура Т = 450 К. Найти
число Маха М = u / а и безразмерную скорость λ = u / а* (а – скорость звука, а* – критическая скорость). Задачу решить по формулам и с помощью таблиц газодинамических функций.
6.17.Скорость воздуха u = 250 м/с, а температура торможения Т0=400К. Найти число М и безразмерную скорость λ. Задачу решить по формулам и с помощью таблиц газодинамических функций.
6.18.Найти критическую скорость а* и критическую температуру Т* для потока воздуха, если температура торможения Т0 = 600 К.
6.19.Поток воздуха имеет скорость u = 200 м/с и температуру
Т = 400 К. Найти критические скорости а* и температуру Т*. Задачу решить по формулам и с помощью таблиц газодинамических функций.
6.20.Поток воздуха имеет при статическом давлении р = 1·105 Па и температуре Т = 500 К скорость u = 150 м/с. Найти критические параметры (давление р, температуру Т и скорость u). Задачу решить по формулам и пр и помощи таблиц газодинамических функций.
6.21.Температура воздуха в баке большого объёма Т0 = 500 К. Температура воздуха в струе, вытекающей из бака, Т1 = 400 К. Какая скорость v потока в струе. Является ли она дозвуковой или сверхзвуковой.
Гидрогазодинамика. Метод. указания к самостоятельной работе |
54 |
