11) Вычисление площади плоской фигуры и объёма тела с помощью двойного интеграла

Если  - ограниченная область плоскости , то ее площадь  вычисляется по формуле т.е. если в области  подинтегральная функция , то значение интеграла (1) численно равно площади области .

Пусть  -неотрицательная, непрерывная функция в замкнутой области . Если  - тело, ограниченное сверху поверхностью , снизу - областью , а сбоку - соответствующей цилиндрической поверхностью с образующей параллельной оси OZ и направляющей, совпадающей с границей области , то объем этого тела равен.

Пусть  - тело, ограниченное сверху поверхностью , снизу - поверхностью , причем проекцией обеих поверхностей на плоскость  служит область , в которой функции  и  непрерывны (и ), то объем этого тела равен.

12) Вычисление площади поверхности с помощью двойного интеграла

Площадь поверхности Ω , заданной уравнением z = f ( x , y )  вычисляется по формуле: где D − ортогональная проекция области Ω на плоскость OXY.

13) Криволинейный интеграл 1-го рода.

Криволинейным интегралом первого типа от функции f(х, у, z) по кривой L называется предел интегральной суммы 2 при  и max  :

  2

14) Вычисление криволинейного интеграла 1-го рода с помощью определённого.

Предположим, что кривая L определяется параметрическими уравнениями x=фи(t), y=Ψ(t), (аьфа<=t<=бета). Кривая L называется гладкой , если функции φ(t) и Ψ(t) обладают непрерывными производными φ’(t) и Ψ’(t) на отрезке [a,b]. Кривую L будем называть кусочно-гладкой, если она непрерывна и распадается на конечное число не имеющих общих внутренних точек кусков, каждый из которых представляет собой гладкую кривую. Если кривая L является кусочно-гладкой кривой, а функция f(x,y) непрерывна на кривой L, то существует криволинейный интеграл первого рода и справедливо равенство: *

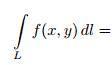
15)Криволинейный интеграл 2-го рода. Физический смысл. Свойства.

Сумму

записывают в виде

и называют криволинейным интегралом II рода (по координатам).

Свойства: 1. Если меняется направление обхода кривой АВ, то интеграл меняет знак.

2.Если кривая АВ состоит из частей, то полный интеграл равен сумме интегралов каждой части.

Физический смысл криволинейного интеграла 2-го рода

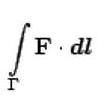- работа силы  при перемещении вдоль пути  . Интеграл по замкнутой кривой обозначают через .

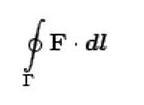16) Вычисление криволинейного интеграла 2-го рода с помощью определённого. Связь между интегралами 1-го и 2-го рода.

Вычисление

Пусть — гладкая, спрямляемая кривая, заданная параметрически (как в определении). Пусть функцияопределена и интегрируема вдоль кривойв смысле криволинейного интеграла второго рода. Тогда

,

,

.

Если обозначить за единичный вектор касательной к кривой, то нетрудно показать, что

Связь между криволинейными интегралами 1-го и 2-го рода. Криволинейные интегралы I и II рода связаны отношением: 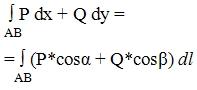"Альфа" и "бета" - углы между касательной кривой с осями Ox и Oy.