Вирішення диференційних рівнянь методом ейлера
Мета практикуму – розробка програмного забезпечення на мові програмування "СІ" для вирішення диференційних рівнянь числовим методом.
ТЕОРЕТИЧНІ ВІДОМОСТІ
1.1. Математична модель електромеханічних систем, електроприводів, технологічних процесів, тобто будь-яких природних об'єктів, явищ та процесів, представляється диференційними рівняннями. Математична модель дозволяє проаналізувати поведінку чи створити ефективну систему керування вказаними системами. Найчастіше в якості аргументу диференційних рівнянь, що описують фізичні процеси, виступає час. Вирішити диференційне рівняння означає отримати закон зміни функції від аргументу, наприклад, закон зміни швидкості кабіни ліфта в часі при підйомі пасажирів із першого на третій поверх. Більшість диференційних рівнянь вирішуються числовими (неаналітичними) методами.
1.2. Звичайне диференційне рівняння I-го порядку має вигляд
(1.1)
де x аргумент;
y невідома функція.
При вирішенні рівняння потрібно знайти залежність y=g(x) при зміні аргументу від відомого початкового значення x0 до відомого кінцевого значення xk при відомому початковому значенні функції y0=y(x0). Найпростішим, але достатньо ефективним методом вирішення рівняння, є метод Ейлера. Для цього аргумент, починаючи з x0, змінюється з фіксованим кроком x
xi+1 = xi + x = xi + H
де i = 0, 1, 2 ... номер кроку обчислень ;
x=H крок обчислень,
а відповідне значення функції yi+1 на кожному кроці знаходиться розкладанням її у ряд Тейлора в точці xi із збереженням членів 1-ої похідної
тобто
yi+1 = yi +Н f(xi, yi)
де yi попереднє та відоме значення функції, яке на початку
обчислень дорівнює y0.
Таким чином, значення функції yi+1 на поточному кроці обчислень xi+1 визначається попереднім значенням функції yi збільшеним (зменшеним) на добуток кроку обчислень Н на значення правої частини диференційного рівняння f(xi, yi) при відомих попередніх значеннях аргументу xi та функції yi. Як видно, метод Ейлера для обчислення значення yi+1 використовує інформацію тільки з одного попереднього кроку xi та yi, тому він називається однокроковим і представляє рекурентну формулу виду
y = y +Н f(x, y) (1.2)
або
y = y +y
де y приріст функції.
1.3. При числовому вирішенні диференційного рівняння реальний графік функції y=g(x) замінюється сумою відрізків прямих на кожному кроці зміни аргументу H, рис. 1.1.
Рис. 1.1.
Чим менше цей крок, тим точніше ламана лінія наближається до реального графіка, проте збільшується кількість циклів та час обчислень. Збільшення кроку зменшує точність обчислень, а при переході через критичне значення взагалі призводить до неприпустимого порушення обчислювального процесу, тому важливим є вибір раціонального кроку, який визначається законами теорії автоматичного керування. Для методу Ейлера локальна похибка обчислень на кожному кроці становить Н2, а сумарна – Н. В рамках даної лабораторної роботи величину кроку доцільно вибирати практичним шляхом у межах від 0,001 до 0,01, порівнюючи результати при різних кроках.
1.4. Приклад 1. Обчислити перехідний процес струму I=f(t) на протязі однієї секунди після подачі на котушку з індуктивністю L=1 Гн та електричним опором R=10 Ом напруги U=220 В. Процес описується наступним диференційним рівнянням
(1.3)
де t – час (аргумент рівняння).
Спочатку рівняння (1.3) записується відносно похідної у формі (1.1)
а потім відповідно до методу Ейлера у вигляді (1.2)
де H – крок зміни часу, задається рівним H=0,0001.
Програма на мові "Паскаль" має наступний вигляд
Program Euler;
Uses Crt;
Const
U= 220; L= 1; R= 10;
H= 0.0001; Tend= 1; Kprint= 50;
Var
I, t , Tprint :real;
Begin
{ Формування заголовка }
TextBackGround (lightgray);
ClrScr;
TextColor (red);
writeln (' ':7, 'ПЕРЕХІДНИЙ ПРОЦЕС СТРУМУ');
writeln;
TextColor (blue);
writeln (' ':9, 'Час, с',' ':4,'Струм, А');
Window (1,4,80,25);
TextColor (white);
{ Початкові умови }
t:=0;
I:=0;
Tprint:=0;
Repeat
{ Вивід даних }
if t >= Tprint then
begin
writeln (' ':9,t:5:3,' ':5,I:7:3);
Tprint:= Tprint+ Kprint*H;
end;
{ Основне рівняння }
I:= I+ H*(U-I*R)/L;
t:=t+ H;
Delay (50);
Until t > Tend+H;
Repeat Until KeyPressed;
End.
Як видно з тексту програми, на екран виводиться не кожне обчислене значення, а тільки кратне заданому значенню коефіцієнта Kprint= 50.
Програма на мові "СІ" для вирішення цієї ж задачі має такий вид:
#include <stdio.h>
#include <conio.h>
#include <dos.h>
void main(void)
{
const float U=220, L=1, R=10, h=0.0001, Tend=1, Kprint=50;
float I,t,Tprint;
clrscr();
printf("\n\n%45s\n\n%27s%27s","Transient current","time,s","Current,A");
t=0;
I=0;
Tprint=0;
do
{
if(t>=Tprint)
{
printf("\n\n%28.5f%24.5f",t,I);
Tprint+=Kprint*h;
}
I+=h*(U-I*R)/L;
t+=h;
delay(3);
}
while(t<=Tend+h);
getch();
}
1.5. Аналогічно вирішується система диференційних рівнянь чи рівняння високого порядку. Проте попередньо їх потрібно привести до системи рівнянь 1-го порядку (нормальна форма Коші)
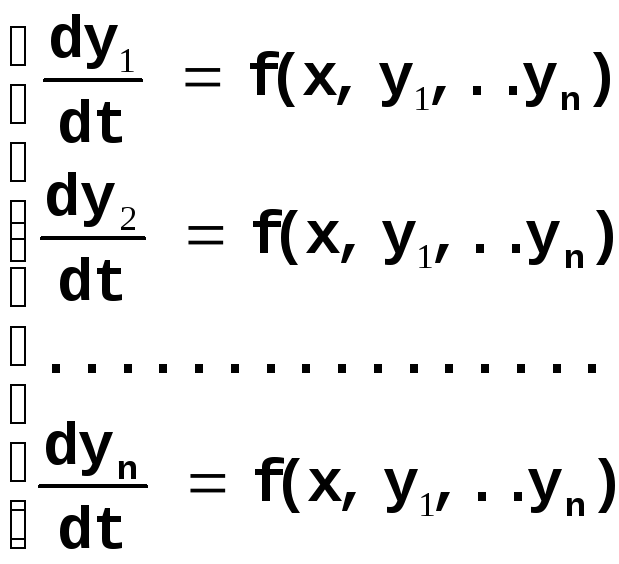(1.4)
Наприклад, необхідно привести рівняння 4-го порядку до системи 4-х рівнянь 1-го порядку
(1.5)
Приведення здійснюється за допомогою заміни y=y1, після чого рівняння (1.5) представляється наступним чином
1.6. При вирішенні системи рівнянь виду (1.4) спочатку обчислюються на поточному кроці значення всіх правих частин рівнянь, а потім значення функцій. Обчислення правих частин зручно оформити у вигляді підпрограми.
1.7. Приклад 2. Обчислити та побудувати графік перехідного процесу струму I=f(t) та швидкості =f(t) двигуна під час його пуску вхолосту. Процес описується наступною системою диференційних рівнянь
де I– струм двигуна, [А];
– кутова швидкість двигуна, [рад/с];
t– час, [с];
U=220 В – напруга живлення;
с=1,5 – конструкційна стала двигуна;
R=0,5 Ом – електричний опір обмотки;
L=0,01 Гн – індуктивність обмотки;
J=0,8 кг*м2 – момент інерції ротора двигуна.
При реалізації метода Ейлера значення невідомих змінних розміщуються в масиві Y розміром за кількістю диференційних рівнянь системи, тобто N=2. При цьому елементами масиву є струм та швидкість двигуна Y[1]=I, Y[2]=. Аналогічно праві частини рівнянь також знаходяться у своєму масиві F, тому його елементи мають значення
Програма на мові "Паскаль" має наступний вигляд
Program Euler_System;
Uses Crt, Graph;
Const
U= 220; L= 0.01; R= 0.5;
c= 1.5; H= 0.001; J= 0.8;
Tend= 1; N= 2; Kprint= 10;
Var
F, Y :array [1..N] of real;
Imax, Wmax, Tprint, t :real;
fn :text;
{ Підпрограма вирішення рівнянь }
Procedure Euler;
Var
K :integer;
{ Обчислення правих частин рівнянь }
Procedure FY;
begin
F[1]:=(U-c*Y[2]-R*Y[1])/L;
F[2]:=c*Y[1]/J;
end;
Begin
{ Формування заголовка }
TextBackGround (lightgray);
ClrScr;
TextColor (red);
writeln (' ':15, 'ПЕРЕХІДНІ ПРОЦЕСИ');
writeln;
TextColor (blue);
writeln (' ':2, 'Час, с',' ':4,' ':4,'Струм, А',
' ':4,'Швидкість, рад/с');
Window (1,4,80,25);
TextColor (white);
{ Початкові умови }
t:=0; Y[1]:=0; Y[2]:=0;
Imax:=0; Wmax:=0; Tprint:=0;
{ Відкриття файлу для запису }
Assign (fn, 'F:\TP\Demo.Out');
Rewrite(fn);
{ Основний цикл обчислень }
Repeat
{ Вивід даних }
if t >= Tprint then
begin
writeln (' ':3,t:5:2,' ':7,Y[1]:7:2,' ':7,
Y[2]:7:2);
writeln (fn, t:5:2,' ':7,Y[1]:7:2,' ':7, Y[2]:7:2);
Tprint:= Tprint+ Kprint*H;
if Y[1] > Imax then Imax:= Y[1];
if Y[2] > Wmax then Wmax:= Y[2];
end;
{ Метод Ейлера}
FY;
for K:=1 to N do Y[K]:=Y[K]+H*F[K];
Delay (500);
t:=t+ H;
Until t > Tend+H;
Window (1,1,80,25);
Close (fn);
End;
{ Підпрограма побудови графіків }
Procedure GRAPHIC;
Var
GraphDriver, GraphMode, ErrorCode :integer;
X, Yu, Yi, Yw, X0, Yu0, Yi0, Yw0, K :integer;
mt, mi, mw, I, W :real;
Begin
{ Відкриття графічного режиму }
GraphDriver:= Detect;
InitGraph (GraphDriver, GraphMode, 'f:\tp\bgi');
ErrorCode:= GraphResult;
if ErrorCode <> grOK then
begin
Writeln (GraphErrorMsg (ErrorCode));
Halt;
end;
{ Формування сітки графіка }
SetBkColor(7);
Rectangle (40, 10, GetMaxX- 10, GetMaxY- 30);
for K:= 1 to 3 do Line (((GetMaxX- 40) div 4)*K+40, 10,
((GetMaxX- 40) div 4)*K+40, GetMaxY- 30);
for K:= 1 to 2 do Line (40, ((GetMaxY-30) div 3)*K,
GetMaxX-10, ((GetMaxY- 30) div 3)*K);
SetColor(red);
SetTextJustify (CenterText, CenterText);
SetTextStyle (SmallFont, HorizDir,5 );
OutTextXY (35, GetMaxY-25 ,'0');
OutTextXY (GetMaxX-15, GetMaxY-25 ,'t');
SetColor(blue);
OutTextXY (20, 15 ,'I');
SetColor(magenta);
OutTextXY (20, 30 ,'W');
SetLineStyle (0,0,3);
{ Визначення масштабів }
mt:= (GetMaxX- 50)/Tend;
mi:= (GetMaxY- 40)/Imax;
mw:= (GetMaxY- 40)/Wmax;
{ Початкові умови }
X0:= 40;
Yi0:= GetMaxY- 30;
Yw0:= GetMaxY- 30;
{ Відкриття файлу для читання }
Assign (fn, 'F:\TP\Demo.Out');
Reset (fn);
{ Основний цикл побуди графіків }
While Not Eof(fn) do
begin
Readln (fn, t,I,W);
X:= 40+ Round (t*mt);
Yi:= GetMaxY- 30-Round (I*mi);
Yw:= GetMaxY- 30-Round (W*mw);
SetColor(blue);
Line (X0, Yi0, X, Yi);
SetColor(magenta);
Line (X0, Yw0, X, Yw);
X0:= X; Yi0:= Yi; Yw0:= Yw;
end;
Close (fn);
Repeat Until KeyPressed;
CloseGraph;
End;
{ Основна програма }
BEGIN
Euler;
Graphic;
END.
Програма на мові "Сі" для вирішення цієї ж задачі має такий вид
#include <stdio.h>
#include <conio.h>
#include <dos.h>
#include <graphics.h>
#include <math.h>
#define N 2
const float U=220, L=0.01, R=0.5, h=0.001, Tend=1, Kprint=10, c=1.5, J=0.8;
float Imax,Wmax,t,Tprint;
float mt,mi,mw;
int X0,Yi0,Yw0,X,Yi,Yw;
float F[N], Y[N];
int k;
int gd=DETECT, gm=0, errorcode;
FILE *pfile;
void main(void)
{
clrscr();
t=0;
Y[0]=0;
Y[1]=0;
Imax=0;
Wmax=0;
Tprint=0;
printf("\n\n%42s\n\n%17s%16s%16s\n\n","Transient speed and current","time,s","Speed rad/s","Current,A");
pfile=fopen("Cdemo.out","w");
do
{
if(t>=Tprint)
{
printf("%18.5f%14.5f%14.5f\n",t,Y[0],Y[1]);
fprintf(pfile,"%18.5f%14.5f%14.5f\n",t,Y[0],Y[1]);
Tprint+=Kprint*h;
if (Y[0]>Imax) Imax=Y[0];
if (Y[1]>Wmax) Wmax=Y[1];
}
F[0]=(U-c*Y[1]-R*Y[0])/L;
F[1]=c*Y[0]/J;
for(k=0;k<=1;k++) Y[k]+=h*F[k];
t+=h;
delay(1);
}
while(t<=Tend+h);
getch();
fclose(pfile);
initgraph(&gd, &gm, "C:\\TC\\BGI");
errorcode=graphresult();
if (errorcode!=grOk)
{
printf("Graphics error: %s\n:",grapherrormsg(errorcode));
printf("Press any key to exit");
getch();
exit(1);
}
rectangle(40,10,getmaxx()-10,getmaxy()-30);
for(k=1;k<=3;k++)
line(((getmaxx()-40)/4)*k+40,10,((getmaxx()-40)/4)*k+40,getmaxy()-30);
for(k=1;k<=2;k++)
line(40,((getmaxy()-30)/3)*k,getmaxx()-10,((getmaxy()-30)/3)*k);
outtextxy(35,getmaxy()-25,"0");
outtextxy(getmaxx()-15,getmaxy()-25,"t");
setcolor(RED);
outtextxy(20,15,"I");
setcolor(MAGENTA);
outtextxy(20,30,"W");
mt=(getmaxx()-50)/Tend;
mi=(getmaxy()-40)/Imax;
mw=(getmaxy()-40)/Wmax;
X0=40;
Yi0=getmaxy()-30;
Yw0=getmaxy()-30;
setlinestyle(SOLID_LINE,0xFFFF,THICK_WIDTH);
pfile=fopen("Cdemo.out","r");
while(!feof(pfile))
{
fscanf(pfile,"%f%f%f\n",&t,&Y[0],&Y[1]);
X=40+(t*mt);
Yi=getmaxy()-30-(Y[0]*mi);
Yw=getmaxy()-30-(Y[1]*mw);
setcolor(MAGENTA);
line(X0,Yw0,X,Yw);
setcolor(RED);
line(X0,Yi0,X,Yi);
X0=X;
Yi0=Yi;
Yw0=Yw;
}
getch();
closegraph();
fclose(pfile);
}
ЗАВДАННЯ НА РОБОТУ
Розробити та запустити у роботу програму на мові програмування "СІ", яка вирішує задачу відповідно до заданого нижче варіанта.
2.1. Тіло падає під дією сили тяжіння з нульової початкової швидкості. Рух описується наступною системою диференційних рівнянь
де х – шлях; V – швидкість; g – прискорення вільного падіння; K=0,5 – коефіцієнт тертя об повітря; t – час.
Вирішити систему рівнянь методом Ейлера та побудувати графіки x=f(t), V=f(t) для проміжку часу від 0 до 5 секунд.
2.2. Процес наведення телескопа за кутом піднесення описується наступною системою диференційних рівнянь
де A, B – кути головного валу та піднесення; U=10 – сигнал завдання; a=2, c=3 – коефіцієнти підсилення; ТА=0,5 с, ТВ=0,8 с – сталі часу; t – час.
Вирішити систему рівнянь методом Ейлера та побудувати графіки A=f(t), B=f(t) для проміжку часу від 0 до 3 секунд.
2.3. Електрична схема постійного струму складається з послідовно з’єднаного джерела ЕРС, котушки індуктивності, конденсатора, резистора та описується наступною системою диференційних рівнянь
де І – струм в електричному колі; UС – напруга на конденсаторі; Е=100 В – ЕРС; R=100 Ом – опір резистора; L=0,01 Гн – індуктивність котушки; С=1 мкФ – ємність конденсатора; t – час.
Вирішити систему рівнянь методом Ейлера та побудувати графіки І=f(t), UС=f(t) від моменту увімкнення джерела ЕРС і до усталення значення UС.
2.4. Переміщення маніпулятора за допомогою електропривода описується наступною системою диференційних рівнянь
де Vх – швидкість та переміщення маніпулятора; U=100 – сигнал завдання; а=2 – коефіцієнт; t – час.
Вирішити систему рівнянь методом Ейлера та побудувати графіки V=f(t), х=f(t) для проміжку часу від 0 до 10 секунд.
2.5. Процес нагрівання повітря в приміщенні за допомогою тепловентилятора описується наступною системою диференційних рівнянь
де Т – температура повітря; N – потужність теплового потоку; Р=1000 Вт – потужність тепловентилятора; А=40, С=80 – тепловіддача та теплоємність; k=10 – коефіцієнт; t – час.
Вирішити систему рівнянь методом Ейлера та побудувати графіки Т=f(t), N=f(t) для проміжку часу від 0 до 10 секунд.
2.6. Обмотка збудження генератора постійного струму живиться від спеціального перетворювача. Ця схема описується наступною системою диференційних рівнянь
де І – струм збудження; U – напруга збудження; UЗ=10 В – напруга завдання; R=0,5 Ом – електричний опір кола; L=0,01 Гн – індуктивність кола; Т=3 с – стала часу; t – час.
Вирішити систему рівнянь методом Ейлера та побудувати графіки І=f(t), U=f(t) для проміжку часу від 0 до 4 секунд.
2.7. Тіло рухається назустріч іншого нерухомого тіла під дією сили притягування з початковою швидкістю V0=0,5 м/с та з початкової відстані х0=2 м. Рух описується наступною системою диференційних рівнянь
де х – шлях; V – швидкість; t – час.
Вирішити систему рівнянь методом Ейлера та побудувати графіки x=f(t), V=f(t) до моменту зіткнення тіл.
2.8. Гальмування тролейбуса при підході до зупинки за допомогою тягового електродвигуна описується наступною системою диференційних рівнянь
де М – момент електродвигуна; – кутова швидкість електродвигуна; R=0,5 Ом – електричний опір обмотки двигуна; L=0,01 Гн – індуктивність обмотки двигуна; с=2 – конструкційна стала двигуна; J=0,2 кг*м2 – сумарний момент інерції двигуна та тролейбуса; t – час.
Вирішити систему рівнянь методом Ейлера та побудувати графіки М=f(t), =f(t) до зупинки тролейбуса від початкової швидкості двигуна 0=90 рад/с та моменту М0=-50 Нм.
2.9. Процес нагрівання двох металічних заготовок у печі описується наступною системою диференційних рівнянь
де Т1, Т2 – температури першої та другої заготовок; Р=3000 Вт – потужність печі; А1=2, А2=3 – тепловіддачі заготовок; С1=10, С2=15 – теплоємності заготовок; t – час.
Вирішити систему рівнянь методом Ейлера та побудувати графіки Т1=f(t), Т2=f(t) для проміжку часу від 0 до 30 секунд.
2.10. За допомогою електродвигуна здійснюється поворот платформи, рух якої описується наступною системою диференційних рівнянь
де – кутова швидкість та кут повороту; U=220 В – напруга живлення двигуна; k=0,5 – коефіцієнт передачі; Т=0,5 с – стала часу; t – час.
Вирішити систему рівнянь методом Ейлера та побудувати графіки =f(t), =f(t) для проміжку часу від 0 до 3 секунд.
КОНТРОЛЬНІ ЗАПИТАННЯ
3.1. В чому полягає суть метода Ейлера.
3.2. Чому метод Ейлера називається однокроковим.
3.3. Як залежить похибка обчислень від величини кроку аргументу.
3.4. Як представити звичайне диференційне рівняння 1-го порядку у формі для його вирішення методом Ейлера.
3.5. Яким чином диференційне рівняння високого порядку приводиться до системи рівнянь 1-го порядку.
СПИСОК РЕКОМЕНДОВАНОЇ ЛІТЕРАТУРИ
Бородич Ю.С., Вальвачев А.Н., Кузьмин А.И. Паскаль для персональних компьютеров.- Минск: Высшая школа, 1991.- 365 с.
Турбо Паскаль 7.0.- К.: Издательская группа BHV, 1996.- 448 с.
Сердюченко В.Я. Розробка алгоритмів та програмування на мові Turbo Pascal.- Х.: ВКП “Парітет” ЛТД, 1995.- 352 с.
Бронштейн И.Н., Семендяев К.А. Справочник по математике.- М.: Наука, 1981.- 718 с.
ДСТУ 3008-95. Документація. Звіти у сфері науки і техніки. Структури і правила оформлення.- К.:Держстандарт України, 1995.- 38 с.
Керниган Б., Ритчи Д. Язык программирования Си.\ пер. с англ., 3-е изд., испр. – СПб.: “Невский Диалект”, 2001. – 352 с.
Подбельский В.В., Фомин С.С. Программирование на языке Си: Учеб. пособие. – 2-ое доп. изд. – М.: Финансы и статистика, 2004. – 600 с.
Додаток А
МІНІСТЕРСТВО ОСВІТИ І НАУКИ, МОЛОДІ І СПОРТУ УКРАЇНИ
НТУУ “Київський політехнічний інститут”
Кафедра автоматизації електромеханічних систем та електроприводу
УМОВНІ ПЕРЕХОДИ НА МОВІ "ПАСКАЛЬ". ЗАВДАННЯ № 1
Комп'ютерний практикум № 2 з кредитного модуля ”Обчислювальна техніка та програмування-1”
Перевірив Виконав
доцент Островерхов М.Я. студент групи ЕП-01
Дорошенко А.В.
Київ 2011
Додаток Б