- •1.Квантова теорія вільних електронів у кристалі.
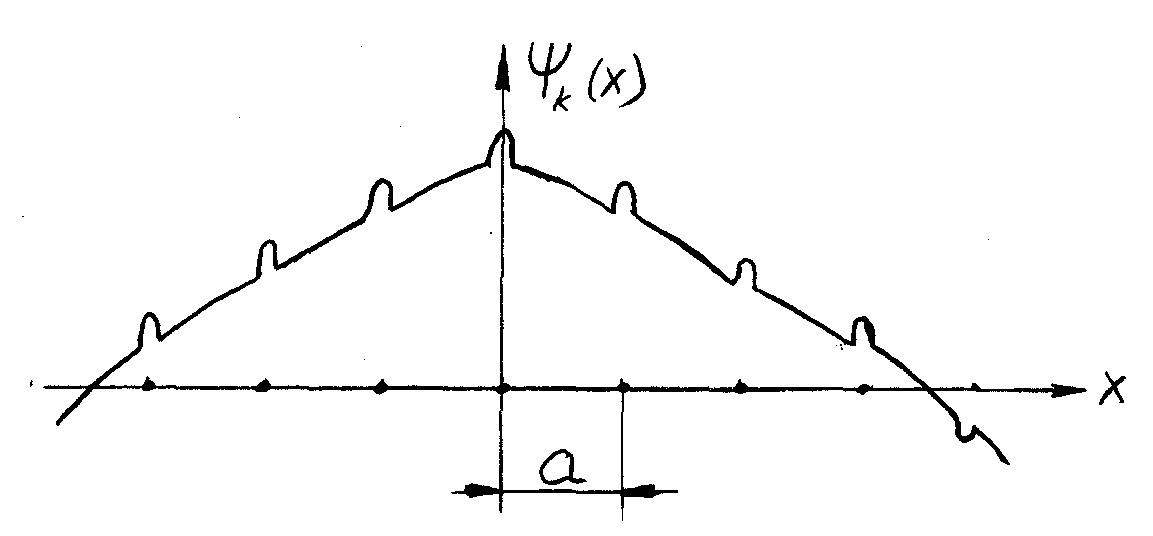
- •Хвильова функція вільних електронів
- •Поверхня Фермі вільних електронів у кристалі.
- •Зони Бріллюена.
- •Провідники з точки зору зонної теорії.
- •Діелектрики з точки зору зонної теорії.
- •Напівпровідники з точки зору зонної теорії.
- •Теорема Блоха.
- •Наслідки теореми Блоха.
- •Циклічні умови Борна-Кармана.
- •Хвильові функції вільних електронів у кристалі.
- •Кількість квантових станів в зоні Бріллюена (густина станів у зоні Бріллюена).
- •Квазіімпульс електрона у кристалі.
- •Ефективна маса електрона у кристалі.
-
Теорема Блоха.
Теорема Блоха:
Хвильову функцію електронів у періодичному полі кристала можна представити у такому вигляді:
![]() (5-4).
(5-4).
![]() -
вектор має розміри обернені довжині
функції
-
вектор має розміри обернені довжині
функції
![]() .
.
![]() -деяка
функція, яка має періодичність гратки.
-деяка
функція, яка має періодичність гратки.
![]() (5-5).
(5-5).
|
|
Функція
(5-5)
![]() називається модулюючим множником.
називається модулюючим множником.
Хвильова функція, яка визначається ф-лою (5-4) називається хвильовою ф-цією Блоха.
Вона являє собою плоску хвилю модульовану в такт гратки.
Вектор![]() називається
хвильовим вектором в кристалі.
називається
хвильовим вектором в кристалі.
-
Наслідки теореми Блоха.
-
Стани електрона в кристалі: ψк(r) та ψk+2πb(r) в межах однієї енергетичної зони фізично еквівалентні:
ψк(r)= ψk+2πb(r) (6.1),
де b - вектор оберненої гратки.
тобто хвильовий вектор k електрона в періодичному полі кристалічної гратки визначений з точністтю до довільного вектора оберненої гратки домноженого на 2π
-
В межах кожної енергетичної зони енергія електрона в кристалі є періодичною функцією хвильового вектора k з періодом 2πb.
-
Циклічні умови Борна-Кармана.
Якщо розміри кристалу в якому знаходяться електрони досить великі, то явища на його поверхні практично не будуть впливати на стан електрона в центрі кристала. Мінімальний об’єм, починаючи з якого виконується вище наведена умова називається основною областю кристалу (V0). Тоді вірним буде таке твердження:
в кристалі будь-якого об’єму більшому ніж V0, фізичні стани електронів повторюються у просторі з періодом, що дорівнює лінійній величині області V0. Це можна довести, якщо з’єднати декілька областей V0 кристалів. Це твердження справедливе, як для полікристалів так і для монокристалів. Експериментальні дані показують, що лінійний розмір основної області має порядок величини 10-6 м.
Дамо математичне формулювання циклічних умов Борна-Кармана. Представимо основну область у вигляді паралелепіпеда:
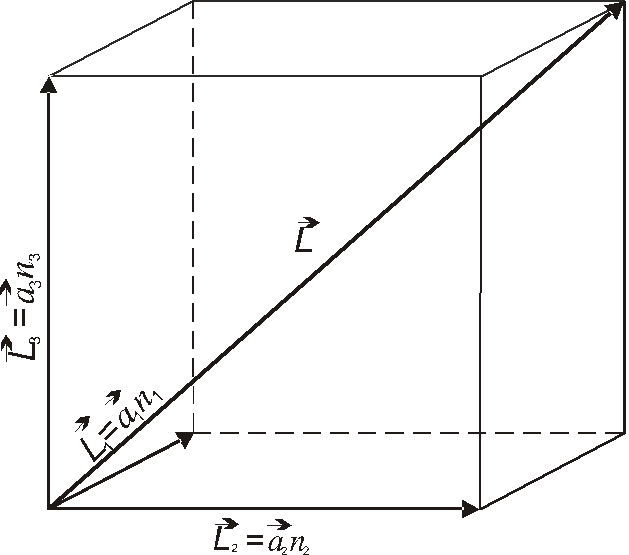
де, n1, n2, n3 – цілі числа порядка 104
![]() - базисні вектори кристалічної гратки
- базисні вектори кристалічної гратки
![]() -
діагональ паралелепіпеда (3-4)
-
діагональ паралелепіпеда (3-4)
Властивість
періодичності функції
![]()
![]() можна записати:
можна записати:
![]() (3-5)
(3-5)
![]() (3-6)
(3-6)
![]() (3-7)
(3-7)
![]() (3-8)
(3-8)
![]() (3-9)
(3-9)
![]() (3-10)
(3-10)
![]() (3-11)
(3-11)
Умови (3-10), (3-11) виконуються при значеннях:

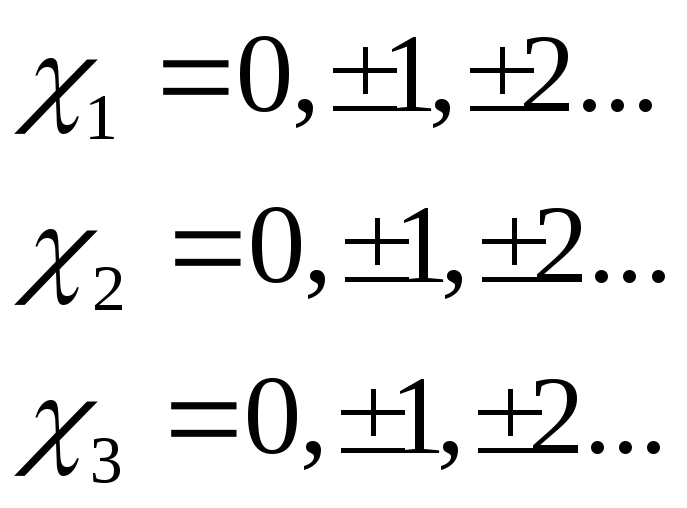 (3-12)
(3-12)
З (3-12) витікає:
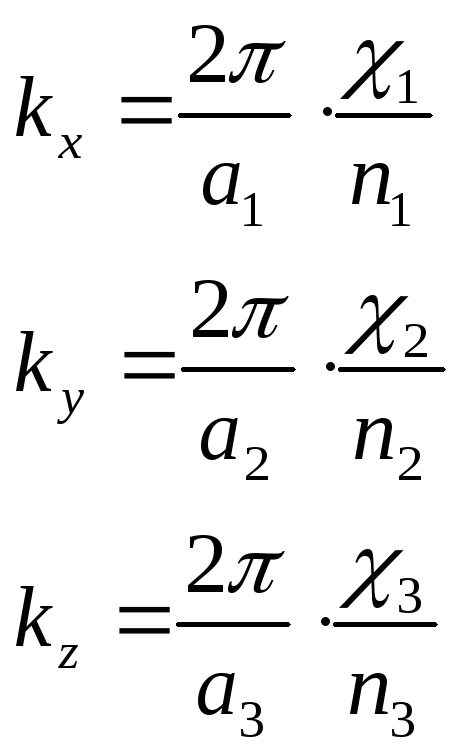 (3-13)
(3-13)
Формули
(3-13) визначають можливі значення складових
хвильового вектора
![]() електрона в кристалі. Оскільки а1,
а2,
а3
та n1,
n2,
n3
фіксовані
для даного кристалу числа, то
електрона в кристалі. Оскільки а1,
а2,
а3
та n1,
n2,
n3
фіксовані
для даного кристалу числа, то
![]() визначаються відповідно числами
визначаються відповідно числами
![]() ,
тобто складові хвильового вектора
змінюються дискретно або мають дискретний
спектр. Відповідно і сам вектор
k
має дискретний спектр.
,
тобто складові хвильового вектора
змінюються дискретно або мають дискретний
спектр. Відповідно і сам вектор
k
має дискретний спектр.