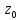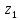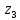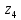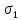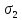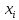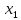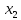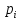Задача№3
АЦП непрерывных сигналов.
m-разрядный АЦП рассчитан на входные напряжения в интервале (Umin, Umax) и проводит квантование во времени с шагом t=1. Записать последовательность, состоящую из 5 двоичных комбинаций на выходе АЦП, если на вход поступает сигнал U(t)=u0+u1t+u2t2, для 0 ≤t≤4. Найти среднеквадратическую величину ошибки квантования по уровню для данного сигнала σ и затем ее теоретическое значение σo=Δu/(√12), где Δu – шаг квантования по уровню. Полученные двоичные комбинации представить в форме целых неотрицательных десятичных чисел Z0,Z1,…,Z4, например: 00011010=26
Исходные данные:
|
№вар |
m |
Umin |
Umax |
U0 |
U1 |
U2 |
|
22 |
8 |
-84.55 |
-8.40 |
-7.30 |
-9.20 |
-2.00 |
На входе данный сигнал выглядит следующим образом:
U(t)=Uo+U1t+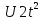 =-7.30-9.20t-
=-7.30-9.20t-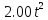 .
.
найдём значение сигнала в заданные моменты времени:
U0=-7.30-9.20*0-2.00*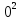 =-7.30;
=-7.30;
U1=-7.30-9.20*1-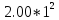 =-18.50;
=-18.50;
U2=-7.30-9.20*2-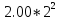 =-33.70;
=-33.70;
U3=-7.30-9.20*3-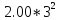 =-52.90;
=-52.90;
U4=-7.30-9.20*4- =-76.10.
=-76.10.
Рассчитаем шаг квантования по уровню:
 .
.
Далее рассчитаем номер интервала, в который входит шаг квантования по уровню(только целая часть):
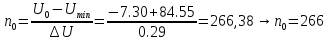 ;
;
 ;
;
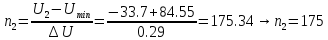 ;
;
 ;
;
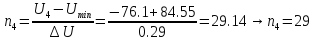 .
.
Запишем полученные номера интервалов в двоичном виде:
 ;
;
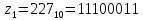 ;
;
 ;
;
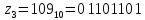 ;
;
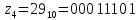 .
.
Далее нам необходимо преообразовать при помощи ЦАП полученную последовательность, в результате чего мы получим эталонные значения:
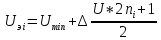 ;
;
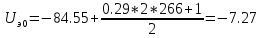 ;
;
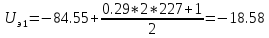 ;
;
 ;
;
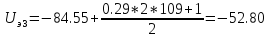 ;
;
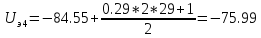 .
.
Рассчитаем ошибку округления:
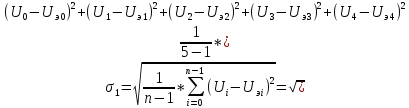 =
=
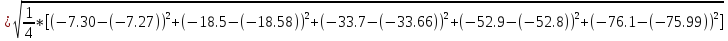 =
=
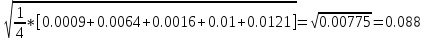 .
.
Теоретическая ошибка квантования составит:
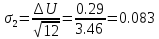 .
.
Как видим
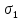 и
и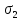 очень близки, что подтверждает правильность
расчётов.
очень близки, что подтверждает правильность
расчётов.
Представим ответы в виде таблицы.
|
|
|
|
|
|
|
|
S |
|
267 |
227 |
175 |
109 |
29 |
0.088 |
0.083 |
807.171 |
Глава 2. Расчётное задание № 2. Задача №1.
Определить информационные характеристики источника и канала, а именно: производительность источника, скорость потери информации в канале, скорость создания в канале ложной информации, энтропию на выходе канала в расчёте на один символ и в ед. времени.
Исходные данные:
Бодовая скорость
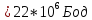 .
.
|
|
X1 |
X2 |
|
Y1 |
0.11 |
0.15 |
|
Y2 |
0.3 |
0.44 |
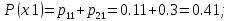

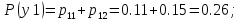
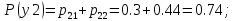
Рассчитаем скорость передачи информации в канале:
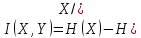 Y)=H(Y)-H(Y/X)=H(X)+H(Y)-H(X,Y)
. (1)
Y)=H(Y)-H(Y/X)=H(X)+H(Y)-H(X,Y)
. (1)
Мощность источника :
H(X)=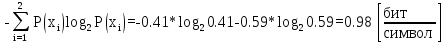 ;
(2)
;
(2)
Энтропия на выходе :
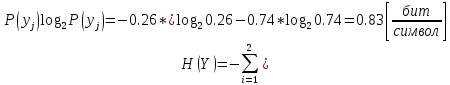 ; (3)
; (3)
Рассчитаем совместную энтропию :
 (4)
(4)
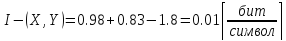 ;
(5)
;
(5)
Скорость потери информации:
H(X/Y)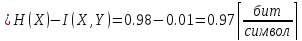 ; (6)
; (6)
Скорость создания ложной информации:
H(X/Y) ; (7)
; (7)
Определим энтропию в расчёте на один символ и в ед.времени :
H(X)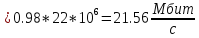 ;
;
H(Y) ;
;
H(X/Y)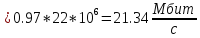 ;
;
H(Y/X)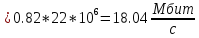 ;
;
Задача №2.
По указанным вероятностям можно найти вероятность третьего значения.
1) Определить энтропию источника и его избыточность.
2)Произвести блоковое кодирование источника блоками по два символа двоичными числами кодами Хаффмана, Шеннона-Фано и равномерным кодом
3) Сравнить коды по эффективности.
4)Определить вероятность появления 0 и 1 в последовательностях символов на выходе кодеров.
Исходные данные:
|
|
|
|
|
|
|
0.11 |
0.15 |
0.74 |
Посчитаем энтропию:
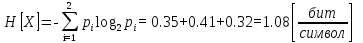 ;
(8)
;
(8)
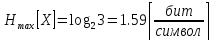 ;
(9)
;
(9)
Также рассчитаем избыточность:
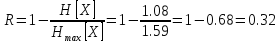 ;
(10)
;
(10)
2. Произведём блочное кодирование по 2 символа:
Код Шеннона-Фано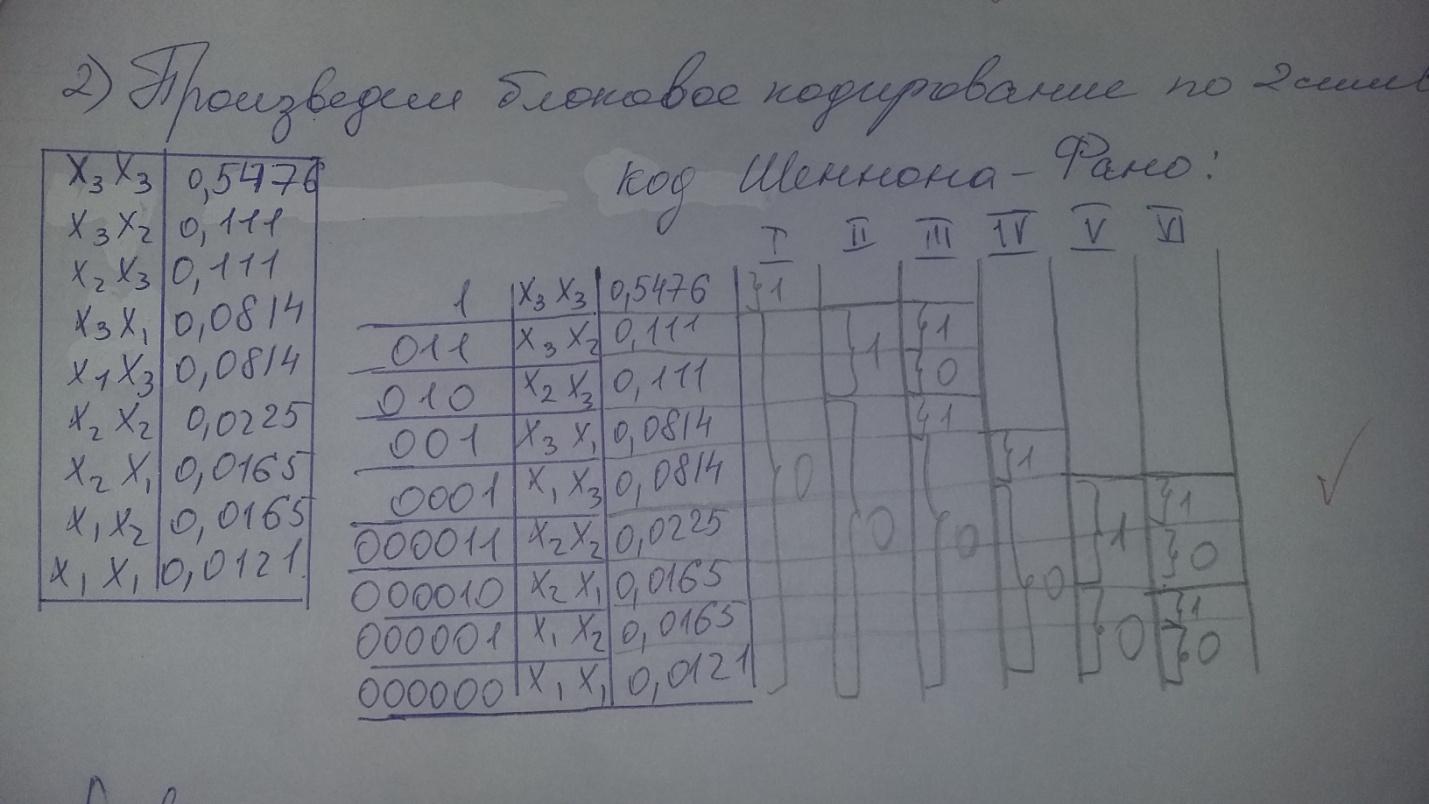
Равномерный код:
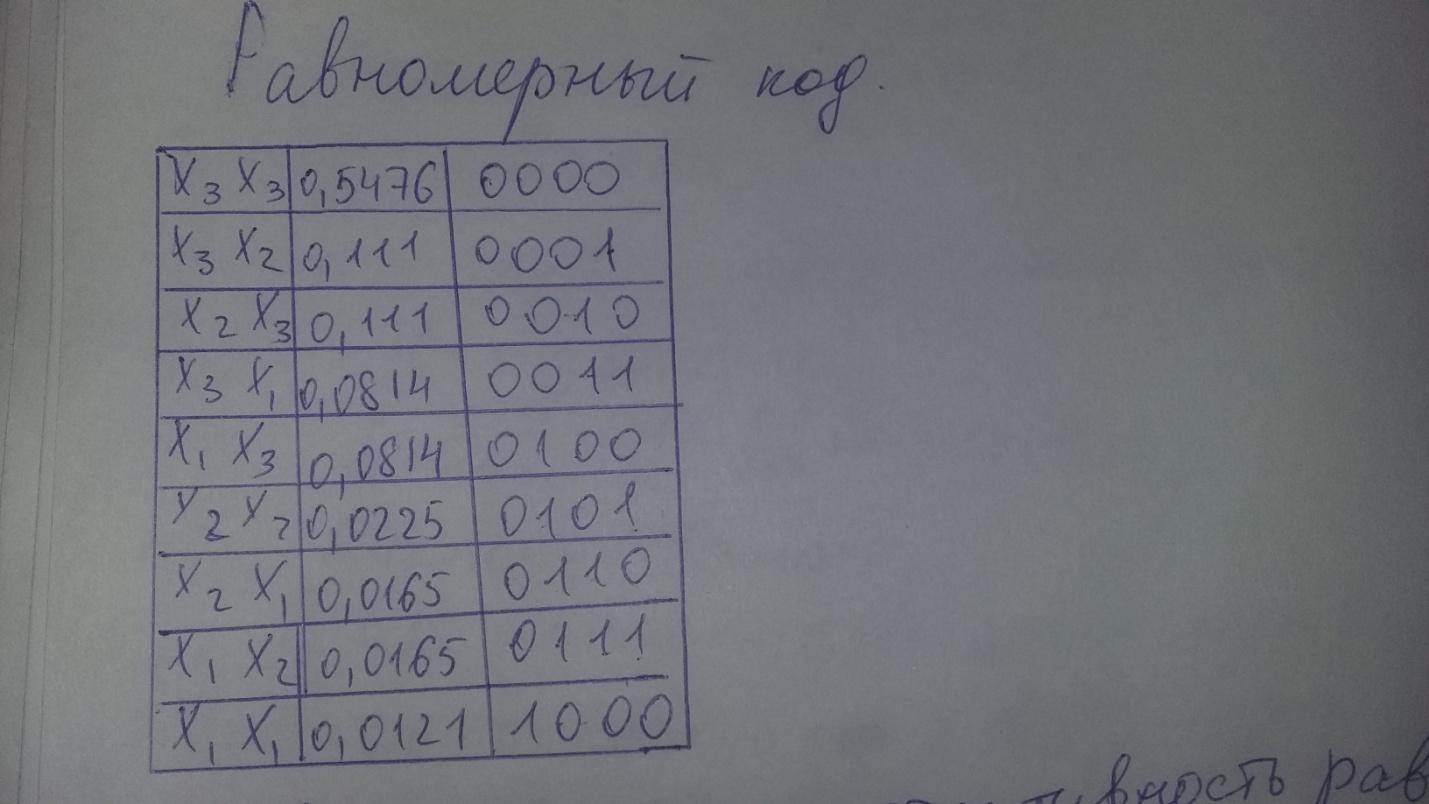
Расчитаем эффективность равномерного кода :
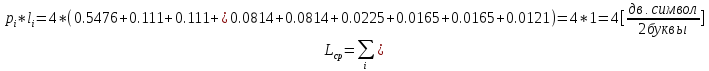 ;
(11)
;
(11)
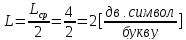 ;
(12)
;
(12)
 ;
(13)
;
(13)
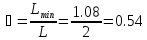 ;
(14)
;
(14)
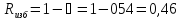 ;
(15)
;
(15)
Код Хаффмана :

Рассчитаем эффективность:
Код Хаффмана
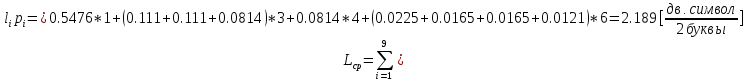 ;
(16)
;
(16)
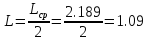
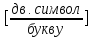 ;
(17)
;
(17)
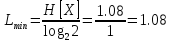
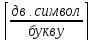 ;
(18)
;
(18)
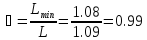 ;
(19)
;
(19)
В таком случае избыточность будет равна :
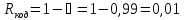 ;
(20)
;
(20)
 ;
(21)
;
(21)
Код Шеннона-Фано
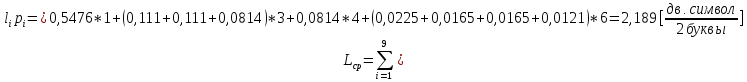 ;
(22)
;
(22)
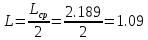
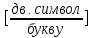 ;
(23)
;
(23)

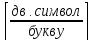 ;
(24)
;
(24)
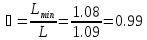 ;
(25)
;
(25)
В моём случае эффективности, при кодировании кодом Хаффмана и Шеннона-Фано, равны. Это совпадение. И мы можем выбрать любое кодирование на наше усмотрение.
Рассчитаем вероятности появления 0 и 1:
Код Хаффмана:
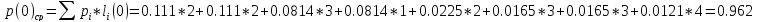
 ;
(26)
;
(26)
p(0)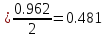
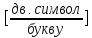 ;
(27)
;
(27)
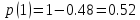
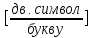 ;
(28)
;
(28)
Код Шеннона-Фано :
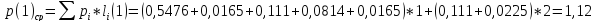
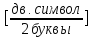 ;
(29)
;
(29)
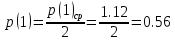
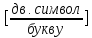 ;
(30)
;
(30)
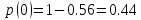
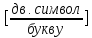 ;
(31)
;
(31)
Равномерный код :
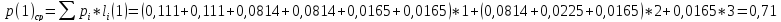
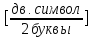 ;
(32)
;
(32)
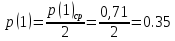
 ;
(33)
;
(33)
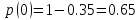
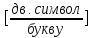 ;
(34)
;
(34)
В кодах Хаффмана и Шеннона-Фано вероятности появления 0 и 1 приблизительно одинакова. Вравномерном коде вероятность появления 0 выше, чем вероятность появления 1.