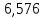Полонская-152-4инд зад
.docxЗадача 1
1) Вероятность битовой ошибки при передаче цифрового сигнала
Источник информации создает цифровой поток B мегабит в секунду. На вход радиолинии с выхода передатчика подается последовательность двоичных радиоимпульсов, модулированных по закону М (М=1 для АМ, М=2 для ЧМ с ортогональными сигналами, М=3 для ФМ). Задана требуемая вероятность битовой ошибки Рош на выходе оптимального когерентного демодулятора Рош и величина ослабления в линии F. На входе приемника присутствует аддитивный белый гауссовский шум со спектральной плотностью No.
Определить требуемую среднюю мощность W передаваемых сигналов обоих видов (0 и 1) без использования корректирующего кода (W1) и при использовании (n,k)-кода Хэмминга в режиме исправления ошибки (W2). Определить в каждом из режимов вероятность битовой ошибки на выходе линии связи (декодера) (PБ1, PБ2 )
Примечания:
1) 1пВт=10-12 Вт.
2) При вычислении отношения сигнал/шум необходимо учитывать, что длительность передаваемых импульсов должна уменьшаться при увеличении избыточности, чтобы обеспечить заданную скорость передачи В информационных символов.
3) Вероятность битовой ошибки при демодуляции двоичного сигнала в когерентной системе определяется по формуле
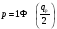 ,
,
где
 – интеграл вероятности,
– интеграл вероятности,
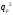 – отношение энергии разностного сигнала
(импульса) к спектральной плотности
мощности белого шума, зависящее не
только от средней мощности сигнала (Pc)
на выходе линии, но и от вида модуляции,
q2=Е/
No
– отношение энергии разностного сигнала
(импульса) к спектральной плотности
мощности белого шума, зависящее не
только от средней мощности сигнала (Pc)
на выходе линии, но и от вида модуляции,
q2=Е/
No
 при
при
 .
.
Обратите внимание, что энергия сигнала зависит не только от его мощности, но и от длительности, E=WT.
Исходные данные:
|
N |
M |
F,дБ |
n |
k |
B,Мбит/с |
Рош*10^2 |
N0,пВт/Гц |
|
22 |
1 |
54 |
63 |
57 |
0,3 |
0,3 |
0,3 |


Ф(q/2)= 0.997

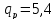
При амплитудной
модуляции величины
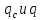 связаны следующим соотношением:
связаны следующим соотношением:
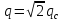 ,
,
 .
.
где
 отношение
средней энергии импульса на входе
демодулятора к спектральной
отношение
средней энергии импульса на входе
демодулятора к спектральной
плотности шума.
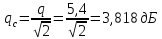 .
.
Известно, что
 ,
где
,
где
 средняя
энергия одного импульса (так как появления
0 и 1 равновероятно).
средняя
энергия одного импульса (так как появления
0 и 1 равновероятно).
 ,
,
Мощность сигнала на входе приёмника можно рассчитать по формуле:
 .
.
где
 время
длительности сигнала;
время
длительности сигнала;
 бодовая
скорость.
бодовая
скорость.
 ,
,
Необходимо также
учесть, что в линии происходит затухание
сигнала, поэтому мощность, дошедшая до
приёмника, в
 раз меньше, чем на передатчике.
раз меньше, чем на передатчике.
В таком случае мощность на передатчике:

2) Необходимо найти
среднюю мощность W
передаваемых сигналов обоих видов (0 и
1) при использовании
 кода
Хэмминга (
кода
Хэмминга ( ).
).
В этом случае в
результате избыточности кода необходимо
за один и тот же промежуток времени
передать больше сигналов, следовательно,
при использовании корректирующего кода
бодовая скорость увеличивается в
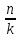 раз.
раз.
 .
.
где
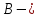 заданная
бодовая скорость,
заданная
бодовая скорость,
 число
информационных символов,
число
информационных символов,
 длина
кодовой последовательности.
длина
кодовой последовательности.
 .
.
 .
.
Учтём затухание в линии передачи:

|
W1
^ |
W2^ |
|
|
S |
|
|
|
|
|
16.605 |
Если учитывать степень и суммиовать в одной и той же степени то сумма ответов S=13.87062
Задача 2
На кабельной линии,
содержащей
 регенерационных
участков, регенерация двоичных импульсов
в полном смысле этого слова проводится
лишь в обслуживаемых регенерационных
пунктах (ОРП), размещенных на каждом
регенерационных
участков, регенерация двоичных импульсов
в полном смысле этого слова проводится
лишь в обслуживаемых регенерационных
пунктах (ОРП), размещенных на каждом
 ом
участке. На остальных участках размещены
необслуживаемые регенерационные пункты
(НРП), в которых входной сигнал лишь
усиливается. Определить вероятность
ошибки при демодуляции сигнала на выходе
некогерентной линии
ом
участке. На остальных участках размещены
необслуживаемые регенерационные пункты
(НРП), в которых входной сигнал лишь
усиливается. Определить вероятность
ошибки при демодуляции сигнала на выходе
некогерентной линии
 ,
если при
,
если при
 эта величина равна
эта величина равна
 ,
,
где
 – отношение сигнал/шум по мощности на
входе первого НРП, а все участки и
– отношение сигнал/шум по мощности на
входе первого НРП, а все участки и
приемники идентичны.
Ошибка возникает только при декодировании сигнала, то есть на обслуживаемых регенерационных пунктах, в ретрансляторах, которыми, по сути, являются (НРП), осуществляется уменьшение отношения сигнал/шум, вследствие этого увеличивается вероятность возникновения ошибки при декодировании.
Исходные данные:
|
N |
m |
n |
q1, дБ |
|
22 |
5 |
20 |
18(7.94) |
Рассчитаем число регенераторов (ОРП):
 ,
итак, на каждый регенератор приходится
,
итак, на каждый регенератор приходится
 ретрансляторов, которые просто усиливают
сигнал.
ретрансляторов, которые просто усиливают
сигнал.
Вероятность возникновение ошибки на входе каждого регенератора (ОРП) можно рассчитать по формуле:
 ,
,
Если число ошибок
в линии чётное, то ошибок нет. Вероятность
появления ошибки на выходе некогерентной
линии
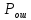 тогда определяется по следующей формуле:
тогда определяется по следующей формуле:
 ,
,
где
 .
.