МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

___________________

Пензенская государственная архитектурно-строительная академия

Определение коэффициента Теплопроводности воздуха Методом нагретой нити

Методические указания к лабораторной работе ФПТ1-3

Пенза 2000

УДК 531.23

ББК 22я7

Составители:	Н.Н.Григорьевский, кандидат технических наук, доцент; А.Г.Денисова, ассистент
Рецензент –	кандидат технических наук, доцент С.В.Голобоков.

Содержат основные сведения о явлении теплопроводности в газах. Опи­са­ны физические величины, характеризующие теплопроводность. Дано теоре­ти­ческое обоснование и изложена методика определения коэффициента тепло­проводности газа методом нагретой нити.

Методические указания подготовлены на кафедре физики и предназначены для использования студентами всех специальностей при выполнении лабо­раторных работ по курсу “Общая физика”.

© Пензенская государственная

архитектурно-строительная академия, 2000

Цель работы

Изучение теплопроводности как одного из явлений переноса в га­зах; освоение методики определения коэффициента тепло­провод­ности газа.

Приборы:

Установка для определения коэффициента теплопроводности воздуха ФПТ1-3.

1.Теплопроводность в газах

Из второго начала термодинамики следует, что во всякой изоли­рованной (т.е. не испытывающей никаких внешних воздействий) системе самопроизвольно протекают только такие процессы, кото­рые приводят ее в состояние, не изменяющееся в дальнейшем с те­че­нием времени. Такое состояние термодинамической системы назы­вается тепловым равновесием. Например, тепло всегда переходит от горячего тела к холодному, пока температуры обоих тел не станут одинаковыми, то есть пока не установится тепловое равновесие.

Если в газе существует пространственная неоднородность плот­ности, температуры или скорости движения отдельных его слоев, то на хаотическое тепловое движение молекул накладывается их упо­рядоченное движение. При этом возникают потоки вещества, энер­гии или импульса. В результате происходит самопроизвольное вы­ра­в­нивание параметров газа. Эти потоки являются физической осно­вой так называемых явлений переноса. К явлениям переноса от­­но­сятся диффузия, теплопроводность и внутреннее трение (вяз­кость). Диффузия обусловлена переносом массы, а внутреннее тре­ние – переносом импульса молекул.

Рассмотрим более подробно теплопроводность. Это явление воз­никает при наличии разности температур, обусловленной внешними причинами. Теплопроводность газа заключается в непосредственной передаче кинетической энергии хаотического молекулярного дви­жения от одних молекул к другим при их соударениях.

Если значения температуры различных слоев газа отличаются друг от друга, то и значения средней кинетической энергии также будут разными. Молекулы, движущиеся из более нагретых частей объема газа, попадая в менее нагретые слои и сталкиваясь с молекулами, имеющими меньшие скорости, передают им часть своей энергии. Так, молекулы из менее нагретых слоев газа уве­ли­чивают свою энергию. Этим объясняется передача тепла в направ­ле­нии убывания температуры. Этот процесс не сопровождается макро­скопическим движением среды.

Для простоты рассмотрим одномерное явление тепло­провод­нос­ти. В этом случае определяющие ее физические величины зависят толь­ко от одной координаты (например координаты ). Пред­поло­жим, что газ заключен между двумя параллельными поверхнос­тя­ми, имеющими температурыи (рис.1).

Если эти температуры под­дер­живать постоянными, то через газ установится стаци­о­нар­ный (т.е. неизменный во времени) поток теплоты. На­правим осьперпендику­ляр­но к этим поверхностям. Не­од­но­родность в пространстве зна­чений температуры может быть задана с помощью градиента. Градиент – это вектор, харак­те­ризующий изменение физи­чес­кой величины (в данном случае температуры) при перемещении на единичную длину и направленный в сторону наиболее быстрого ее возрастания. Таким образом, вдоль осибудет иметь место градиент температуры. Количество теплоты, передаваемое вследствие теплопроводности за времячерез поверхность пло­щадью, расположенную перпендикулярно оси, опре­деляется за­коном Фурье:

, (1.1)

где –	коэффициент теплопроводности;
–	градиент температуры.

Знак минус показывает, что перенос тепла происходит в на­правлении убывания температуры.

Количество теплоты, переносимое через поверхность площадью за одну секунду, называется тепловым потоком:

.

Из формулы (1.1) следует, что

.

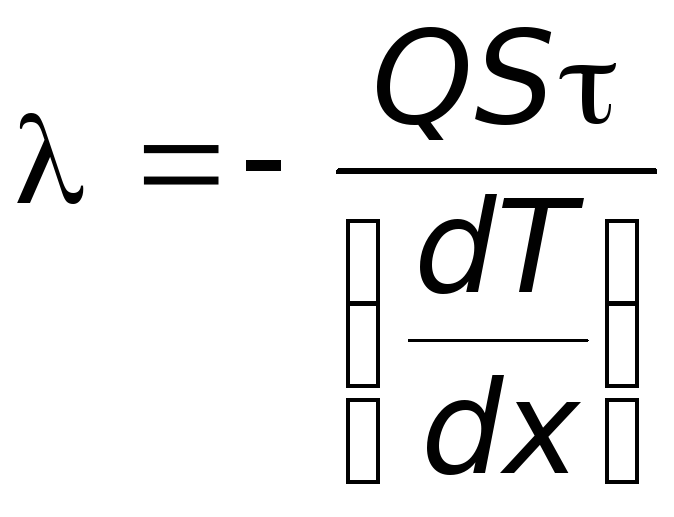Отсюда видно, что коэффициент теплопроводности численно ра­вен количеству теплоты, проходящему через единицу площади по­верхности за единицу времени при градиенте температуры, равном единице.

Выведем размерность этой физической величины:

.

Коэффициент теплопроводности показывает, насколько быстро вы­равнивается температура различных точек газа. Чем больше коэф­фициент теплопроводности, тем скорее наступает состояние теп­лового равновесия. Коэффициент теплопроводности зависит от агрегатного состояния вещества, его атомно-молекулярного строе­ния, температуры, давления и состава. В анизотропных средах он зависит от направления распространения тепла.

Наилучшие проводники тепла – твердые тела, в особенности металлы. Влияние давления на теплопроводность твердых тел с хорошей степенью точности описывается линейной зависимостью. У многих металлов и минералов теплопроводность растет с ростом давления. В процессе плавления металлов теплопроводность, как правило, падает скачком при температуре плавления.

Жидкости обычно проводят тепло намного хуже твердых тел. Так, коэффициент теплопроводности воды при температуре 0 ⁰С со­ставляет 0,55, а льда 2,21. Как правило, теплопро­вод­ность жидкостей убывает с ростом температуры и слабо возрастает с ростом давления.

Газы обладают наименьшей теплопроводностью по сравнению с жидкостями и твердыми телами. Например, при 20 ⁰С коэффициент теплопроводности углекислого газа равен 0,0162, водорода 0,175, воздуха 0,0257.

Выведем формулу для нахождения коэффициента теп­ло­проводности идеального газа. Выделим элементарную площадку , расположенную перпендикулярно оси(см. рис. 1).

В соответствии с формулой (1.1) элементарное количество теп­лоты , переносимое молекулами через площадкуза время, равно

. (1.2)

Учтем, что до площадки долетают только те молекулы, кото­рые находятся от нее не дальше длины свободного пробега моле­кулы газа. Средняя длина свободного пробега – это среднее рас­с­тояние, которое пробегает молекула между двумя после­до­ва­тельными столкновениями. Она вычисляется по формуле

,

где –	эффективный диаметр молекулы – минимальное расстоя­ние, на которое сближаются при столкновении центры молекул;
–	концентрация молекул.

Выберем на оси две точки А и В, расположенные по обе сто­роны площадкина расстояниях от нее, равных средней длине свободного пробега молекулы газа(см. рис.1). Будем считать, что температура в месте, где находится площадка, равна, а.

Тогда температура в точке А равна , а в точке В.

Найдем число молекул, проходящих за одну секунду через по­верхность . Поскольку процесс теплопроводности не сопро­вож­дается макроскопическим движением среды, количество молекул, пересекающих эту поверхность в единицу времени слева на­право и справа налево, будет одинаковым. Ввиду хаотичности теп­лового движения можно считать, что вдоль каждой из осей коор­динат (а значит, и вдоль оси) движется со скоростьюодна треть от общего количества молекул. Из них половина движется слева направо, а половина – справа налево.

Следовательно, количество молекул определяется по формуле

, (1.3)

где –	концентрация молекул;
–	среднеарифметическая скорость теплового движения молекул газа:

;

здесь–	постоянная Больцмана;
–	масса одной молекулы;
–	молярная масса газа;
–	универсальная газовая постоянная;
–	площадь выделенной поверхности.

Согласно закону равномерного распределения энергии по степеням свободы каждая молекула обладает средней кинетической энергией , вычисляемой по формуле

, (1.4)

где –	число степеней свободы молекулы;
–	постоянная Больцмана;
–	удельная теплоемкость газа при постоянном объеме, вы­числяемая по формуле ;
–	абсолютная температура;
–	масса одной молекулы.

Эта энергия определяется температурой газа в той точке пространства, в которой произошло ее последнее столкновение с другой молекулой.

Энергия , которой обладают молекулы газа, находящиеся в единице объема, равна

. (1.5)

Тогда количество теплоты , перенесенное через площадкуслева направо за время, окажется равным суммарной энергии молекул, имеющих температуру точки А:

. (1.6)

Количество теплоты , перенесенное через площадкуза вре­мясправа налево, равно суммарной энергии молекул, имею­щих температуру точки В:

. (1.7)

Вычитая из выражения (1.7) выражение (1.6), получим общее количество теплоты, перенесенное через площадку :

. (1.8)

Учитывая, что ,

где –	концентрация молекул;
–	масса одной молекулы;
–	плотность газа,

получим окончательное выражение:

. (1.9)

Сравнивая выражения (1.9) и (1.2), получим выражение для коэффициента теплопроводности идеального газа:

. (1.10)

Поскольку длина свободного пробега молекул обратно про­пор­циональна давлению газа, а плотностьпрямо пропорцио­наль­на давлению, то теплопроводность идеального газа от давления не зависит.

Теплопроводность газов зависит от температуры. При увели­чении температуры возрастает энергия каждой молекулы, а значит, и количество энергии, переносимое из слоя в слой. Вместе с тем одновременно увеличивается и число столкновений молекул, что несколько снижает обмен энергией между слоями. В результате коэффициент теплопроводности идеального газа оказывается про­пор­циональным квадратному корню из абсолютной температуры.

Коэффициент теплопроводности реальных газов представляет собой довольно сложную функцию температуры и давления. При­чем, с ростом температуры и давления значение коэффициента теп­ло­­проводности возрастает.

На плохой теплопроводности газов основано применение в строительстве пористых материалов (т.е. материалов, содержащих газовые включения). Этим же объясняются теплоизолирующие свойст­ва одежды, в особенности шерстяной и меховой. В ней содер­жится большое число маленьких пузырьков воздуха, так же, как и в рыхлом снеге, защищающем посевы от вымерзания.