5.3. Межгрупповая и внутригрупповая дисперсии
На вариацию признака влияют различные факторы, которые делятся на случайные и систематические. В статистике определяется количественное воздействие случайных и систематических факторов при помощи различных видов дисперсий.
Предположим, совокупность S разбита на непересекающиеся группы S1, S2, S3 …Sn по возрастанию признака.
Рисунок 5.1. Совокупность разбита на n непересекающихся групп
Дисперсия всей совокупности называется общей дисперсией, она характеризует колебания признака под воздействием всех факторов случайных и систематических. Дисперсия каждой группы, на которые разбита совокупность, называется внутригрупповой. Она рассчитывается по обычной формуле дисперсии:
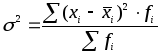(5.13).
Средняя арифметическая из внутригрупповых дисперсий называется средней внутригрупповой дисперсией, характеризует влияние случайных факторов на величину общей вариации, т.е. всех факторов, за исключением того, который положен в основу группировки:
(5.14)
где
– дисперсия каждой группы;
–объем каждой
группы.
Межгрупповой дисперсией (5.15) называется средняя арифметическая квадратов отклонений групповых средних от общей средней величины, характеризует влияние систематических факторов, положенных в основу группировки на величину общей вариации.
Систематические – это факторы, положенные в основы группировки.
(5.15)
где
– групповые средние;
– общая средняя;
–объем каждой
группы.
Правило сложения дисперсий
Если совокупность разбита на непересекающиеся группы S1, S2, S3,…,Sn, то общая дисперсия равна сумме межгрупповой и средней из внутригрупповых дисперсий.
(5.16)
Это - 4-й способ нахождения дисперсии.
Отношение межгрупповой дисперсии к общей, выражаемое в процентах, называется коэффициентом детерминации.
(5.17)
Корень квадратный из него характеризует долю общей вариации, обусловленную влиянием признака, положенного в основу группировки, в общей совокупности всех факторов, и называется эмпирическое корреляционное отношение (5.18):
(5.18)
Пример: имеются данные о производительности труда 10 работников в зависимости от стажа работы.
Таблица 5.1. Стаж и производительность труда работников
|
Стаж работы |
Количество услуг в смену |
Количество работников |
|
менее 5 лет |
11, 8, 9, 12, 11, 9 |
6 |
|
5 лет выше |
9, 12, 10, 13 |
4 |
Определить, как сильно зависит выработка работников от стажа их работы?
1.
2.
3.
4.
5.
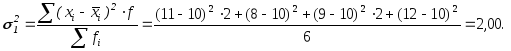
6.
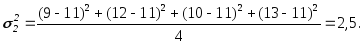
7.
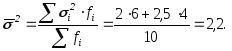
8.
9.
10.
Вывод : производительность труда на 3,13% зависит от стажа работы, а на 96,87 % от прочих факторов.
5.4. Дисперсия альтернативного признака
Если в совокупности исследуется доля единиц, обладающих тем или иным альтернативным признаком, то дисперсия этой доли определяется по формуле
(5.19)
Введем обозначения:
- Наличие признака - через 1,
- Отсутствие признака - через 0,
- Доля единиц, обладающих признаком, – р,
- Доля единиц, не обладающих признаком, – q.
(5.20)
(5.21)
(5.22)
Контрольные вопросы и задания
1. Дайте определение вариации.
2. Назовите показатели вариации.
3. Чем отличается среднее линейное отклонение от среднего квадратического? Какое между ними существует соотношение?
4. Перечислите свойства дисперсии.
5. Что показывает коэффициент вариации?
6. Можно ли использовать среднюю величину при коэффициенте вариации, равном: а) 48%; б) 60%; в) 90%.
7. Какие факторы влияют на вариацию признака?
8. Поясните правило сложения дисперсий.
9. Как определяется дисперсия альтернативного признака?
10. Какие способы расчета дисперсии Вы знаете?