Т2 Аналитические представления

Содержательные сведения о структуре спектра линейного оператора и его собственных векторах можно получить, если конкретизировать класс рассматриваемых операторов. Учитывая прикладную направленность данной работы, с этой целью рассмотрим понятие оператора ограниченной сложности.

Для определения оператора ограниченной сложности рассмотрим сначала понятие полной ограниченности множеств в полном векторном пространстве U . С этой целью приведем определение -сети множества.

Пусть Uc - некоторое множество в пространстве U и - некоторое положительное число. Множество E из U называется -сетью для Uc , если для любой точки u Uc найдется хотя бы одна точка a E такая, что

u a .

является ограниченным множеством, но не обладает полной ограниченностью. Действительно, в бесконечномерном пространстве

lim u 0 .

С физической точки зрения вполне ограниченное множество обладает ограниченной -энтропией. С технической точки зрения сложность реализации подобного множества ограничена. С вычислительной точки зрения подобное множество образует компакт, в котором любая бесконечная последовательность решений имеет сходящуюся подпоследовательность. В вычислительной математике для того, чтобы множество допустимых решений задач было компактным, применяются специальные методы регуляризации. В этом случае процедуры решения задач будут сходиться.

Определение. Оператор LA , отображающий полное векторное

пространство U в себя, называется вполне непрерывным, если он каждое ограниченное множество переводит во вполне ограниченное.

Рассмотрим задачу вычисления значений оператора LA :

y = LAu ; u, y U .

Для решения данной задачи будем использовать проекционные методы. В этом случае вектора u, y с заданной точностью приближенно представляются конечными рядами разложения по базисным векторам

127

Множество Ucn называется вполне ограниченным подмножеством

конечной размерности пространства U , если для него при любом 0

существует конечная -сеть и любой вектор данного множества допускает разложение в конечный ряд по базисным векторам.

Определение. Вполне непрерывный оператор LA , отображающий

полное векторное пространство U в себя, называется оператором ограниченной сложности, если он каждое вполне ограниченное подмножество конечной размерности п переводит во вполне ограниченное подмножество.

На основе сказанного приближенную вычислительную схему

взаимно-ортогональными и нормированными.

Примем в качестве ортонормированного базиса конечномерного пространства Un , которому принадлежат вектора проекций u , y (

Будем полагать, что для рассматриваемого класса операторов при

последовательном повышении точности вычислений:

0 1 2 ... k ... 0,

lim k 0;

k

справедливы предельные переходы

128

быть поставлены в однозначное соответствие с точностью до координатных базисов соответствующих пространств U , U . Другими словами, спектральные характеристики операторов LA и LA совпадают без

ссылки на конкретные системы координат пространств U и U .

вектора u и выходного вектора y на координатные вектора { 1, 2 , ...} ортогонального нормированного базиса пространства U , составленного из собственных векторов оператора LA .

В общем случае спектр оператора LA будет иметь более сложный

характер. В этих случаях спектральное представление оператора требует более детального рассмотрения.

Изучение собственных векторов и собственных значений линейных операторов имеет значительный практический интерес. Как следует из вышеприведенного материала, выражения для преобразовательных свойств линейного оператора значительно упрощаются, если в качестве координатных векторов взять его собственные векторы. Кроме того, собственные значения линейного оператора выражают важные свойства этого оператора, не ссылаясь на какую бы то ни было конкретную систему координат.

2.4.6. Структурные операции над динамическими объектами.

Динамические системы со сложной структурой в общем случае могут быть представлены как результаты применения операций соединения составляющих их динамических объектов. В зависимости от вида

129

соединения можно определить функциональные свойства соединений объектов в целом, исходя из частных функциональных свойств отдельных объектов, входящих в соединение.

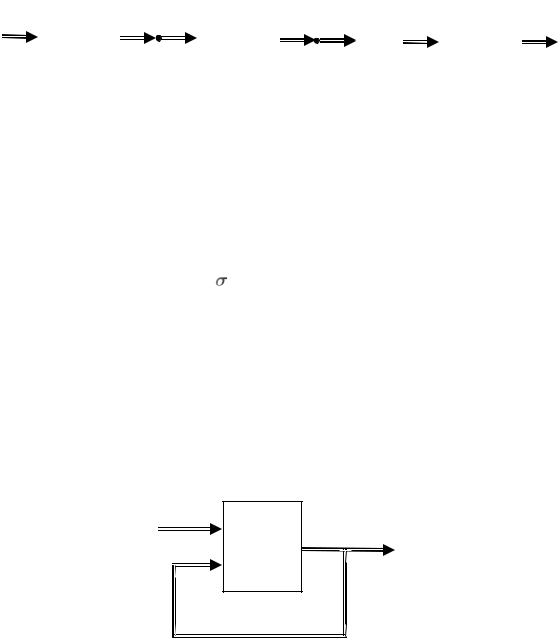
Так, при последовательном соединении объектов (рис. 2.4.10)

Рис. 2.4.10. Последовательное соединение динамических объектов (здесь 1, 2 - узлы соединения)

функциональные свойства соединения в целом описываются композицией выходных функций yi = Gi(σi, ui) объектов:

уn = Gn(σn, Gn-1(σn-1, . . . G2(σ2, G1(σ1, у0)) . . . )),

где yi - переменная, принимающая значения на реализациях выходных процессов для i -го объекта; i - состояние i -го объекта. В общем случае

указанные переменные являются реализациями процессов произвольной природы, при этом функции Gi, связывающие данные переменные, рассматриваются как отображения общего вида.

Более сложные ациклические соединения объектов сводятся к множеству последовательных соединений, для которых может быть применена операция композиции выходных функций.

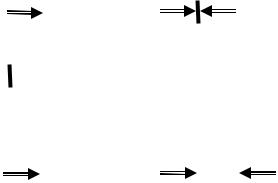
Принципиально иной случай возникает для циклических соединений объектов. Так, рассмотрим базовую конструкцию – охват обратной связью объекта (рис. 2.4.11)

и1

y

и2 G

Рис. 2.4.11. Охват динамического объекта обратной связью

Здесь объект с выходной функцией y = G(σ, (и1, и2)) охвачен обратной связью и2 = у. В результате функциональные свойства объекта определяются решением уравнения

y = G(σ, (и1, y)).

130

Разница приведенных выше выражений проявляется при анализе поведения объектов. Для схемы соединения (рис. 2.4.10) при заданном входном воздействии у0 нахождение неизвестной реакции уn сводится к последовательному вычислению значений выходной функции Gi , т.е. прямой задачи анализа. В случае обратной связи необходимо решение обратной задачи анализа, состоящей в решении соответствующих функциональных уравнений.

Обратные задачи динамики объектов можно представить структурно в виде схемы (рис. 2.4.12). Здесь unknown – неизвестная реализация входного процесса u, которую необходимо определить, исходя из заданной реализации выходного процесса y yт (constraint). Другими словами,

необходимо решить функциональное уравнение

G(u) yт .

В общем случае ставится на решение функциональная задача общего вида

G(u) R yт ,

где R – логическое условие, например, односторонние и двусторонние неравенства.

R – знак логического условия уRyт b)

Рис. 2.4.12. Структурные представления обратной задачи динамики объекта

В общем случае результирующая выходная функция соединения объектов в систему может быть определена на основе операций композиции выходных функций и решения функциональных уравнений, отражающих прямые и обратные связи объектов в структуре соединения их в систему.

131

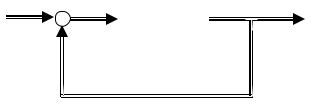
Характеристики объектов с обратными связями можно описать более конструктивно, если дополнительно предположить, что для значений переменных определены операции сложения (+) и вычитания (-). Тогда операция охвата обратной связью объекта может быть выполнена следующим образом (рис 2.4.13).

Рис. 2.4.13

Здесь знаками + (-) отмечены положительная и отрицательная обратная связь соответственно. Таким образом, и = h ± y.

Для рассматриваемого случая можно записать в явном виде выражения для выходной реакции объекта, охваченного обратной связью. С этой целью введем следующие операции над выходными функциями:

- применение функции G к вектору и,

Gи = G(σ, и);

- композиция функций G1, G2, G3, Gп,

GпGп-1 . . . G3G2G1и;

- сложение функций,

(G1 + G2)и = G1(σ1, и) + G2(σ2, и); - вычитание функций,

(G1 - G2)и = G1(σ1, и) - G2(σ2, и); - единичная функция,

Iи = и;

- правая обратная функция,

GG-1п = I;

- левая обратная функция,

G-1лG = I.

Различие между левой и правой обратной функцией состоит в следующем.

Левая обратная функция дает решение уравнения

Gи = у,

в виде

и = G-1лу.

Правая обратная функция, исходя из соотношения

и= G-1пу,

врезультате применения прямой функции G позволяет восстановить исходное уравнение

132

Gи = GG-1пу = у.

Для функции G существует обратная функция G-1 при выполнении условия

G-1л = G-1п = G-1.

Приведенные выше операции в совокупности с множеством располагаемых выходных функций образуют алгебру выходных функций. Используя операции алгебры выходных функций, можно для сложных структур соединений объектов в систему определять их результирующую выходную функцию в виде алгебраического выражения. Так для объекта, охваченного обратной связью (рис. 2.4.13), результирующая выходная функция будет иметь вид

- для положительной обратной связи

y= G(I – G)-1h;

-для отрицательной обратной связи

y= G(I + G)-1h.

Из рассмотрения данных выражений следует, что наличие обратных связей в структуре соединений объектов приводит к обращению выходных функций составляющих объектов. Принимая во внимание, что рассмотрение обратных связей представляет характерную черту системного подхода к исследованию сложных объектов, становится ясно, что анализ сложных объектов должен основываться на решении прямых и обратных задач анализа функциональных свойств составляющих объектов.

2.5. Решение обратных задач

Вычислительные задачи в математической теории систем в общем случае могут быть разделены на два класса: прямые задачи анализа и обратные задачи анализа.

Типовой прямой задачей анализа является проверка выполнения ограничений, наложенных на характеристики рассматриваемой системы. Математически совокупность указанных характеристик можно представить в виде системы уравнений и неравенств

Здесь x – вектор переменных, представляющих параметры анализируемой системы; fi (x) – скалярные функции, представляющие характеристики

системы в зависимости от вектора параметров x ; ai , bi – заданные

ограничения на характеристики системы.

Прямая задача анализа состоит в следующем.

10. Дано конкретное значение xk вектора параметров x анализируемой системы.

133

20. Определить значения вектора параметров x из условия выполнения системы уравнений и неравенств (4).

Таким образом обратная задача сводится к решению системы уравнений и неравенств (4).

К обратным задачам относятся также оптимизационные задачи. Постановку оптимизационных задач можно представить в следующем виде

extr g(x),

Здесь g(x) – целевая функция, экстремум которой необходимо достичь

выбором соответствующих экстремальных значений вектора x при ограничениях (4).

Экстремальная задача (5) может быть сведена к серии задач решения систем уравнений и неравенств, например, для случая минимизации целевой функции

может быть сведено к решению соответствующей экстремальной задачи. В этом случае система уравнений и неравенств (4)

рассматривается как аналитическое представление области допустимых

134

выражено как расстояние до этой области. С этой целью можно использовать, например, квадратичную невязку решения системы уравнений и неравенств (4)

Решение системы уравнений и неравенств (4) определяется как решение экстремальной задачи минимизации квадратичной невязки (7):

Решение задачи (8) может быть выполнено, например, на основе рекуррентной процедуры градиентного метода

xk xk 1 gradQ(xk 1), k 1, 2, ...;

gradQ(xk 1) fi (xk 1) ai grad fi (xk 1) ai fi (xk 1) grad fi (xk 1)

i I ур

fi (xk 1 ) bi grad fi (xk 1).

i Iнер

Здесь – коэффициент релаксации, который выбирается из условия сходимости рекуррентной процедуры.

Если в результате решения задачи (8) минимальное значение невязки (7) равняется нулю, то поставленная задача решения системы уравнений и неравенств (4) выполнена. В противном случае искомое

система уравнений и неравенств считается несовместной, а сама постановка задачи противоречивой.

_____________________________

Рассмотрим более подробно задачи в противоречивых постановках.

135

Прежде всего обратим внимание, что классическая постановка задач оптимизации состоит из двух базовых компонент: целевой функции и ограничений, определяющих область допустимых решений. При этом последовательные процедуры решения указанных задач определяют пошаговый процесс оптимизации величины целевой функции в рамках заданных ограничений. Данный процесс имеет логический предел при достижении критических ограничений, препятствующих дальнейшей оптимизации значений целевой функции. Этот предел может носить формальный характер. В действительности процесс оптимизации в ряде случаев может быть продолжен. В случаях, когда ставится задача дальнейшей оптимизации значений целевой функции, целевая функция с требуемым «запредельным» значением преобразуется в разряд ограничений задачи выбора решений. В результате полученная система ограничений становится противоречивой и формально несовместной. В этих условиях выбор решений осуществляется в два этапа. На первом этапе решается задача формирования требуемой области допустимых решений, в более общем плане – синтеза допустимых решений. На втором этапе решается собственно задача оптимизации. С математической точки зрения формирование допустимых решений может быть выполнено, например, на основе решения несовместных систем уравнений и неравенств.

Несовместные системы уравнений и неравенств являются формальными моделями выбора решений в противоречивых условиях. Подобные модели могут быть использованы при решении задач исследования операций при дефиците располагаемых ресурсов, оптимизации управления по инженерным критериям, построении эмпирических зависимостей с интервальной точностью, синтеза систем управления с гибкой адаптивной структурой и др. Рассмотрим процедуру решения несовместных систем уравнений и неравенств.

В каноническом виде42 постановка задачи решения систем уравнений и неравенств имеет следующий вид.

Дана несовместная система уравнений и неравенств

непрерывные и дифференцируемые функции.

42 Канонический вид равенств и неравенств предполагает, что исходные равенства и неравенства на основе эквивалентных преобразований приводятся к единому виду, когда все равенства равны нулю, а неравенства меньше нуля.

136