
- •Филиал федерального государственного бюджетного образовательного учреждения
- •Оглавление
- •1.0.Введение
- •2.0.Моделирование функции преобразования средства измерения
- •2.1. Задание № 1. Чувствительность средства измерения.
- •2.2. Задание № 2. Определение погрешностей в виде касательной.
- •2.3. Задание № 3. Определение погрешностей в виде хорды.
- •2.4. Задание № 4. Определение погрешностей функции .
- •2.5. Задание № 5. Определение погрешностей функции .
- •2.6. Задание № 6. Определение погрешностей функции .
- •2.7. Задание № 7. Определение погрешностей функции .
2.5. Задание № 5. Определение погрешностей функции .
Аппроксимировать
функцию преобразования СИ на интервале:
![]() линейной функцией вида:
линейной функцией вида:![]() ,
так, чтобы наибольшая погрешность
линеаризации была минимальна:
,
так, чтобы наибольшая погрешность
линеаризации была минимальна:![]() .
Определить предельные относительную
и приведенную погрешности линеаризации.
.
Определить предельные относительную
и приведенную погрешности линеаризации.
Аппроксимируем
функцию преобразования
![]() СИ на интервале [0 ;xн]
= [0 ; 1] линейной функцией yл
= E·x
+ F:
СИ на интервале [0 ;xн]
= [0 ; 1] линейной функцией yл
= E·x
+ F:
Запишем выражение для абсолютной погрешности:
![]()
Приравняв производную абсолютной погрешности по x к нулю, найдём точки, в которых абсолютная погрешность имеет экстремумы:
![]()
![]()
![]()

По условию задачи
подходит точка x2
(во втором случае x1
< 0, т.к. a
>0, c
>0 E
> 0,
![]() )
)
Найдём погрешности в начальной x0, экстремальной x1 и конечной xн точках:
![]()
![]()
![]()
![]()
Оптимизируем решение:
составим систему уравнений с учётом знаков абсолютной погрешности в точках x0, x1 и xн :

Из первого уравнения системы находим E:
![]() ;
E=0.08
;
E=0.08
Из второго уравнения системы находим F:
 Таким образом,
Таким образом,
yл = 0,08x+1,19165

Абсолютная погрешность линеаризации примет вид:
![]()
Предельное значение абсолютной погрешности равно:
![]()
Относительная погрешность линеаризации имеет вид:
![]()
Предельное значение относительной погрешности равно:
![]()
Найдём приведённую погрешность линеаризации:
![]()
2.6. Задание № 6. Определение погрешностей функции .
Аппроксимировать
функцию преобразования СИ на интервале:
![]() линейной функцией вида:
линейной функцией вида:![]() ,
так, чтобы дисперсия погрешности
аппроксимации была минимальна.
Определить предельную приведенную
погрешность линеаризации.
,
так, чтобы дисперсия погрешности
аппроксимации была минимальна.
Определить предельную приведенную
погрешность линеаризации.
Аппроксимируем
функцию преобразования
![]() СИ на интервале [0 ;xн]
= [0 ; 1] линейной функцией yл
= E·x
+ 1,2:
СИ на интервале [0 ;xн]
= [0 ; 1] линейной функцией yл
= E·x
+ 1,2:
Запишем выражение для абсолютной погрешности:
![]()
Найдём дисперсию погрешности аппроксимации по формуле:


Найдём каждый интеграл в отдельности:





![]()
Приравняв производную дисперсии по Е к нулю, найдём значение Е, при котором дисперсия минимальна:
![]()
![]()
![]()
Таким образом,
yл = 0,0645x + 1,2
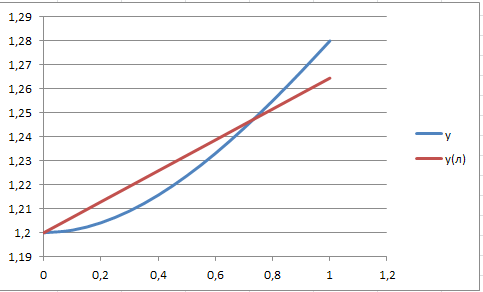
При Е = 0,0645 дисперсия принимает значение:
![]()
Найдём предельную приведённую погрешность линеаризации:
![]()
2.7. Задание № 7. Определение погрешностей функции .
Аппроксимировать
функцию преобразования СИ на интервале:
![]() линейной функцией вида:
линейной функцией вида:![]() ,
чтобы дисперсия погрешности аппроксимации
была минимальна. Определить предельную
приведенную погрешность линеаризации.
,
чтобы дисперсия погрешности аппроксимации
была минимальна. Определить предельную
приведенную погрешность линеаризации.
Аппроксимируем
функцию преобразования
![]() СИ на интервале [0 ;xн]
= [0 ; 1] линейной функцией yл
= E·x
+ F:
СИ на интервале [0 ;xн]
= [0 ; 1] линейной функцией yл
= E·x
+ F:
Запишем выражение для абсолютной погрешности:
![]()
Найдём дисперсию погрешности аппроксимации по формуле:

 Найдём каждый
интеграл в отдельности:
Найдём каждый
интеграл в отдельности:




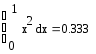


Получаем:
![]()
Приравняв частные производные дисперсии по E и по F к нулю, найдём значения E и F, при которых дисперсия минимальна:
 →
→

Из первого уравнения системы:
F = 1,243-0,666E
Подставляем во второе:

F = (2,45826-0,0834)/2=1,1876
Таким образом,
yл = 0.0834x + 1,1876

При E = 0,0834 и F = 1,1876 дисперсия принимает следующее значение:
![]()
Найдём предельную приведённую погрешность линеаризации:
![]()
-
Лист
