
- •Типовой расчет «теория вероятности и математическая статистика»
- •3. Случайная величина х задана функцией распределения
- •4. Случайная величина х задана функцией плотности
- •3. Случайная величина х задана функцией распределения
- •4. Случайная величина х задана функцией плотности
- •3. Случайная величина х задана функцией распределения
- •4. Случайная величина х задана функцией плотности
- •3. Случайная величина х задана функцией распределения
- •4. Случайная величина х задана функцией плотности
- •3. Случайная величина х задана функцией распределения
- •4. Случайная величина х задана функцией плотности
- •3. Случайная величина х задана функцией распределения
- •4. Случайная величина х задана функцией плотности
- •3. Случайная величина х задана функцией распределения
- •4. Случайная величина х задана функцией плотности
- •3. Случайная величина х задана функцией распределения
- •4. Случайная величина х задана функцией плотности
- •3. Случайная величина х задана функцией распределения
- •4. Случайная величина х задана функцией плотности
- •3. Случайная величина х задана функцией распределения
- •4. Случайная величина х задана функцией плотности
- •3. Случайная величина х задана функцией распределения
- •4. Случайная величина х задана функцией плотности
- •3. Случайная величина х задана функцией распределения
- •4. Случайная величина х задана функцией плотности
- •3. Случайная величина х задана функцией распределения
- •4. Случайная величина х задана функцией плотности
- •3. Случайная величина х задана функцией распределения
- •4. Случайная величина х задана функцией плотности
- •3. Случайная величина х задана функцией распределения
- •4. Случайная величина х задана функцией плотности
- •3. Случайная величина х задана функцией распределения
- •4. Случайная величина х задана функцией плотности
- •3. Случайная величина х задана функцией распределения
- •4. Случайная величина х задана функцией плотности
- •3. Случайная величина х задана функцией распределения
- •4. Случайная величина х задана функцией плотности
- •3. Случайная величина х задана функцией распределения
- •4. Случайная величина х задана функцией плотности
- •Библиографический список
3. Случайная величина х задана функцией распределения
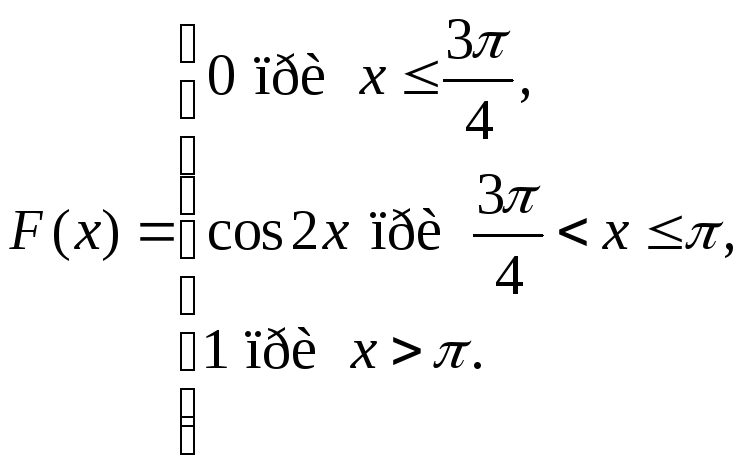
Найти: а) плотность
вероятности f(x);
б) M(x);
в) D(x);
г) σ(x);
д) P(α < x < β),
α = ![]() 0,5,
β = π. Построить графики F(x)
и f(x).
0,5,
β = π. Построить графики F(x)
и f(x).
4. Случайная величина х задана функцией плотности
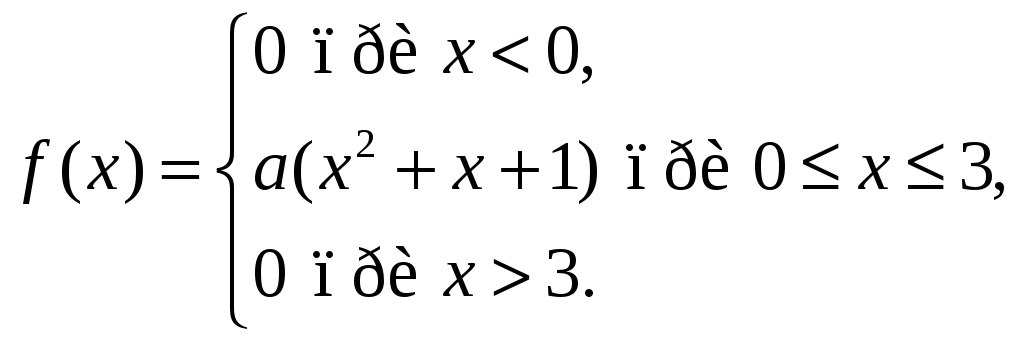
Найти: а) коэффициент а; б) F(x). Построить графики F(x) и f(x).
5. Найти: а) вероятность попадания случайной величины Х, распределенной нормально, в заданный интервал (α; β), если известны М(х) = m и σ(х) = σ; б) вероятность того, что |х – m| < δ, если α = 4, β = 9, m = 2, σ = 5, δ = 8.
6. Построить доверительный интервал для среднего значения (математического ожидания) случайной величины, распределенной по нормальному закону с неизвестными М(х) и σ2(х) по данным выборки (n = 50).
Используя критерий Пирсона, проверить гипотезу о том, что генеральная совокупность Х распределена нормально. Уровень значимости α = 0,05.
|
3,967 |
3,940 |
– 1,836 |
– 2,157 |
– 1,556 |
|
4,865 |
5,865 |
5,393 |
1,723 |
– 2,330 |
|
1,261 |
2,404 |
0,972 |
0,080 |
2,142 |
|
– 4,740 |
1,448 |
4,399 |
0,653 |
8,242 |
|
8,413 |
– 2,600 |
3,737 |
0,479 |
– 3,831 |
|
7,311 |
3,343 |
0,987 |
1,687 |
2,167 |
|
0,588 |
– 0,098 |
6,183 |
– 0,082 |
3,356 |
|
9,221 |
– 5,210 |
3,229 |
0,076 |
4,350 |
|
– 0,305 |
5,242 |
0,061 |
1,142 |
11,926 |
|
1,252 |
2,834 |
1,459 |
1,450 |
– 2,317 |
7. Найти выборочное
уравнение прямой
![]() регрессии y
на x
по данным корреляционной табл. 7.
регрессии y
на x
по данным корреляционной табл. 7.
Таблица 7
|
x y |
5 |
10 |
15 |
20 |
25 |
30 |
ny |
|
8 |
3 |
3 |
|
|
|
|
6 |
|
18 |
|
5 |
4 |
|
|
|
9 |
|
28 |
|
|
40 |
2 |
8 |
|
50 |
|
38 |
|
|
5 |
10 |
6 |
|
21 |
|
48 |
|
|
|
4 |
7 |
3 |
14 |
|
nx |
3 |
8 |
49 |
16 |
21 |
3 |
∑=100 |
Вариант 8
-
a)Известно, что в каждом испытании вероятность появления события А равна р = 0,9, n = 4, m = 3. Найти вероятность того, что в n независимых испытаниях событие А появится: а) ровно m раз; б) не менее m раз; в) не более m раз; г) хотя бы один раз.
b)При бросании двух игральных кубиков два игрока поспорили: если в сумме выпадет число очков, кратное 5, то выигрывает первый игрок, если – 6, то выигрывает второй игрок. У кого из игроков больше шансов выиграть?
c)В коробке лежит 8 красных карандашей и 4 синих. Из коробки наугад вынимают 5 карандашей. Какова вероятность того, что 3 из них окажутся красными, а 2 синими?
d)В квадрат вписан круг радиуса r. Определить вероятность того, что взятая в квадрате точка будет принадлежать кругу.
e) Среди 150 лотерейных билетов есть 8 выигрышных. Найти вероятность того, что из двух наудачу выбранных билетов хотя бы один окажется выигрышным.
2. Найти закон распределения случайной величины X, которая принимает только два возможных значения: x1 с известной вероятностью р1 = 0,9 и x2, причем х1 < х2, М(X)=2,2 и D(X)=0,36.
