
- •Раздел I. Измерение ю.П. Воронов, н.П. Ершова Общие принципы социологического измерения
- •Измерение как установление соответствия двух систем
- •Определение шкалы
- •Обобщённое понятие измерения
- •Типы шкал
- •Типы шкал и социологическое измерение
- •Р.В. Рывкина, м.И. Черемисина о программе построения словаря социологической терминологии
- •Построение словника
- •Выявление основных подходов, зафиксированных в источниках
- •Отбор эмпирического материала.
- •Методы анализа текстов
- •В. И. Герчиков взаимное ориентирование социологических шкал
- •Измерение изменений с учетом структуры множества
- •В.И.Герчиков о пропорционализации шкал социологических признаков
- •Раздел II. Типология в.Л. Устюжанинов проБлема классификации в социологии и теория информации
- •Разбиение множества признаков на подмножества
- •Правила построения графов парных информаций:
- •Объединение подмножества множества α
- •Об иерархии групп объектов в исследуемой совокупности
- •Неявные допущения
- •Динамика групп, определенных разделяющим признаком
- •Изменение мер во времени и образование "Супергрупп"
- •Е.Е. Горяченко обработка ранговых шкал и выделение типичных групп
- •Раздел III. Моделирование в.Н. Рассадин, в.М. Соколов об одной схеме построения математических моделей социальных объектов
- •Ю.П. Воронов, н.П. Москаленко о модедировании адаптации молодежи к труду
- •Г.В. Розанов возможный подход к описанию динамики социальной системы
- •J.P. Voronov, n.P. Yershova
- •E.V. Ryvkina, m.I. Cheremisina
- •V.I. Gerchikov
- •V.G. Ustiuzhaninov
- •Information measures and their application in sociological analysis
- •V.I. Gerchikov
- •V.Q. Ustiuzhaninov
- •V.N. Rassadin, V.M. Sokolov
Объединение подмножества множества α
После
исключения из α пустых подмножеств и
перенумерации получим
![]() .
После исключения из rq градаций,
соответствующих пустым подмножествам
α, и перенумерации получим
.
После исключения из rq градаций,
соответствующих пустым подмножествам
α, и перенумерации получим![]() и
и![]() .
.
Пусть пройдено S шагов объединения и делается S + 1 шаг. На шаге S вычислена матрица вида

Рис.3.
Здесь
![]() – разностное информационное отношение
для подмножеств
– разностное информационное отношение
для подмножеств![]() и
и![]() из
из![]() ,
где αs
= d1
– S.
,
где αs
= d1
– S.
1.
В Q(s),
исключая диагональные элементы, находится
минимальный элемент и соответствующие
ему подмножества объединяются. После
перенумерации получаем
![]() .
.
2.
Вычисляется величина
 ,
где
,
где![]() информация признака
информация признака![]() о признакеXz
о признакеXz
98
на
шаге S
+ 1, а
![]() – их совместная энтропия.
– их совместная энтропия.
3. Если R(s) < R(s+1) то для множества α(s+1) вычисляется матрица Q(s+1) и делается шаг S+2, иначе объединение должно быть прекращено на шаге S.
Выведем
некоторые свойства, необходимые для
алгоритма объединения. Обозначим
минимальный элемент Q(s),
найденный по пункту 1, как
 .
Понадобятся следующие равенства:
.
Понадобятся следующие равенства:
![]() (1)
(1)
![]() (2)
(2)
![]() (3)
(3)
![]() (4)
(4)
Здесь
![]() — потеря информации;
— потеря информации;![]() — потеря энтропии;
— потеря энтропии;![]() — потеря совместной энтропии;
— потеря совместной энтропии;![]() и
и![]() — признаки при объединении наиболее
одинаковых по
— признаки при объединении наиболее
одинаковых по![]() элементов из α. Введем обозначение
элементов из α. Введем обозначение

4.
Если
![]() ,
то
,
то![]() ;
;
Если
![]() ,
,![]() ;
;
Если
![]() ,
,![]()
Докажем только первое утверждение.
99
Из
(1) и (3) следует, что
![]() равносильно
равносильно или
или![]()
Используя
(4) и равенство
![]() ,
получим
,
получим
5.
Если
![]() и
и![]() ,
то
,
то![]() ,
т.е.
,
т.е.![]()
Если
покажем, что
 то утверждение будет доказано. Используя
(1) и (2), получим
то утверждение будет доказано. Используя
(1) и (2), получим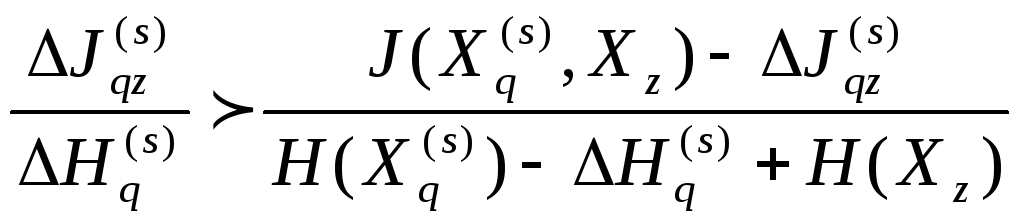
После несложного преобразования это неравенство переходит в первое условие.
6.
Если
![]() и
и![]() ,
то
,
то![]() ,
т.е.
,
т.е.![]()
Доказывается аналогично свойству 5.
7.
Если на первом шаге объединения
![]() и на каждом шаге объединения выполняется
неравенство
и на каждом шаге объединения выполняется
неравенство![]() ,
то
,
то
100
![]() ;
;
![]() ;
;![]() ;
;![]() ;
;![]() ;
;![]() ;
;![]() ;
;![]() .
.
Очевидно,
что
![]() и
и![]() .
Найдем
.
Найдем![]() .
.![]() ,
,![]() и следовательно
и следовательно![]() .
.
Напишем матрицу вида

Из
Q(1)
видно, что подмножества объектов
![]() и
и![]() наиболее близки друг к другу по Хz,
так как элемент
наиболее близки друг к другу по Хz,
так как элемент
![]() матрицыQ(1)
минимален среди недиагональных элементов.
матрицыQ(1)
минимален среди недиагональных элементов.
Объединим
подмножества
![]() и
и![]() .
Получим признак
.
Получим признак![]() с множеством градаций
с множеством градаций![]() .
Здесь
.
Здесь![]() – градация, полученная в результате
объединения
– градация, полученная в результате
объединения![]() и
и![]() .
Нетрудно получить:
.
Нетрудно получить:![]() ;
;![]() ;
;![]() ;
;![]() ;
;![]() ;
;![]() ;
;![]() ;
;![]() ;
;![]() ;
;![]() ;
;![]() ;
;![]()
101
Составим матрицу

Так
как элемент
![]() матрицыQ(2)
минимален среди недиагональных элементов,
то объединим подмножества объектов
α(4)
и α(3).
Получим признак
матрицыQ(2)
минимален среди недиагональных элементов,
то объединим подмножества объектов
α(4)
и α(3).
Получим признак
![]() с множеством градаций
с множеством градаций![]() .
Не трудно подсчитать, что
.
Не трудно подсчитать, что![]() ;
;![]() ;
;![]() ;
;![]() ;
;![]() ;
;![]() ;
;![]() ;
;![]() ;
;![]() .
.
Если
объединить последние две градации в
Х(3),
то получим признак
![]() с одной градацией. В этом случае
с одной градацией. В этом случае![]() ;
;![]() и
и![]()
График
![]() как функцииS
представлен на рис. 4 и имеет тот же вид,
что и на рис. 3. Это понятно, так как
как функцииS
представлен на рис. 4 и имеет тот же вид,
что и на рис. 3. Это понятно, так как
![]() .
.

102
Очевидно, что при S = 3 следует прекратить объединение подмножеств объектов. Выпишем для иллюстрации распределения условных вероятностей до и после объединения.
До объединения:
![]() ;
;
![]() ;
;![]() ;
;![]() ;
;![]() ;
;![]() ;
;![]() ;
;![]() ;
;
После объединения:
![]() ;
;
![]() ;
;
![]() ;
;![]() .
.
Дополним список свойств разностного информационного отношения.
1. Если множество объектов αi одинаково по Xz с множествами αj и αk, то множества объектов αj и αk одинаковы по Xz.
Если Qij(Xq,Xz) = Qik(Xq,Xz) = 0, то Qjk(Xq,Xz) = 0.
На основании свойства 4 пишем, что
![]() ;
l
= 1,2,…,tz;
;
l
= 1,2,…,tz;
![]() ,
откуда
,
откуда
![]() ,
т.е.
,
т.е.![]() .
В частности, отсюда следует, что если,
αi
– непустое множество и строка (столбец)
i
в матрице Q(s)
нулевая, то матрица Q(s)
будет нулевой матрицей.
.
В частности, отсюда следует, что если,
αi
– непустое множество и строка (столбец)
i
в матрице Q(s)
нулевая, то матрица Q(s)
будет нулевой матрицей.
Следующее
ниже свойство 2 означает, что если в М
есть признак, не зависящий от множества
признаков
![]() ,
то при объединении конечных групп в
классы он будет игнорироваться.
,
то при объединении конечных групп в
классы он будет игнорироваться.
Выделим
из М
признак Хψ
и образуем множество Мψ
, которое есть М
без Хψ
и имеет эквивалентный
![]() .
.
103
2.
Если признак Хψ
независим от эквивалентного признака
множества
![]() ,
то
,
то
![]() (5)
(5)
Пусть
![]() иХψ
имеют множества градаций
иХψ
имеют множества градаций
![]() и
и![]() ,
где
,
где![]() и
и![]() – количества градаций по признакам
– количества градаций по признакам![]() иХψ
соответственно. Достаточно показать,
что
иХψ
соответственно. Достаточно показать,
что
![]() .
.

Из
независимости Хψ
от
![]() следует, что
следует, что
![]() ,
,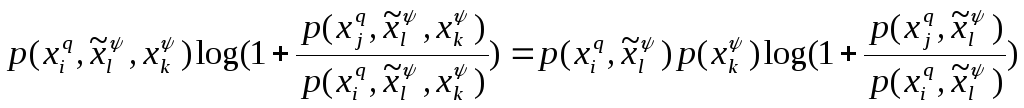
Подставляя
последнее в формулу для
![]() ,
получим требуемое равенство (10).
,
получим требуемое равенство (10).
Выделим
из множества F
признаков N
признак Хψ
и образуем Nφ,
которое есть N
без Хφ.
Эквивалентный признак Nφ
назовем
![]() .
Введем
.
Введем![]() и
и![]() .
.
104
Рассмотрим
множества объектов αij
и αik,
которые по
![]() попадают в одну градацию
попадают в одну градацию![]() ,
а по признакуХφ,
попадают в градации
,
а по признакуХφ,
попадают в градации
![]() и
и![]() соответственно.
соответственно.
3.
Если признак Хφ
независим от эквивалентного признака
множества признаков
![]() ,
то
,
то
![]() дляj,k
= 1,2,…,tφ
(6)
дляj,k
= 1,2,…,tφ
(6)
Из
независимости Хφ
от
![]() ,
следует, что
,
следует, что
 ,
т.е. что
,
т.е. что
Найдем,
что
 ;
;
![]() ;
;
![]()
т.е. равенство (6) доказано.
105
