В.И.Герчиков о пропорционализации шкал социологических признаков
За последние десятилетия в прикладной и теоретической математике появилось много работ, посвященных вычислению и оценке коэффициентов связи признаков с различными шкалами. Особенно много внимания сейчас уделяется шкалам неметрическим – номинальным или порядковым (ранговым). При этом наблюдается очень простая и интересная, на наш взгляд, закономерность. Почти все методы, созданные для оценки и вычисления тех или иных коэффициентов связи различных шкал (коэффициенты простой и ранговой корреляции, конкордации и т.п.), можно применять для решения в некотором смысле "обратных'' задач, а именно задач измерения и шкалирования, т.е. построения таких шкал, которые обладали бы нужным нам свойством: метрикой, порядком, линейностью и т.п.
Предыдущая статья автора в данном сборнике была посвящена методу построения ранговых шкал (их взаимному ориентированию) путем постановки задачи, обратной проверке связи направлений двух шкал. Данная статья продолжает эту традицию, и здесь мы обсудим проблему взаимной пропорционализации ранговых шкал. Как и в первой статье, мы сделаем это путём постановки задачи, обратной оценке пропорциональности двух шкал. В этом смысле данная статья является фактическим продолжением предыдущей и, как и та, является развитием идей, изложенных автором в докладе на Всесоюзном совещании по применению количественных методов в социологии, состоявшемся в апреле 1967 г. в г.Сухуми.
87
Итак,
возьмем две ранговые шкалы S-
того и q-того
признаков длины n
и n
соответственно. Будем считать, что
взаимное ориентирование шкал уже
проведено. Шкалы S
и q
будем считать пропорциональными,
если перемещению на некоторое число
делений i
по одной шкале соответствует перемещение
на пропорциональное число делений j
= i
по другой.
Как и ранее, условимся считать n
n
.
Как
и в случае проверки связи направлений
шкал S-
того и q-того
признаков, будем перебирать все пары
значений признаков в нашей выборке N
и накапливать
характеристическое число
,
изменяя его каждый раз на коэффициент
,
характеризующий информацию о
пропорциональности шкал S
и
q, вносимую
k-той
парой выборки N
: (i
,
j
),
где i
-значение
шкалы q-того
признака в этой паре. Процесс описывается
формулой
=
+
(I)
Задача,
следовательно, сводится к построению
шкалы
.
Рассмотрим
построение шкалы приращений
на примере для случаяn
=
7 и n
= 5.
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
1
1
1
|
1 |
|
2 |
|
3 |
|
4 |
|
5 |
88
При
пропорциональных шкалах на деление I
шкалы q
приходится
целиком деление I и 25
деления 2 шкалы S;
на деление 3 шкалы q
- 35
деления 2 и 45
деления 3 шкалы S;
на деление 3 шкалы q
- 15
деления 3, целиком деление 4 и 15
деления 5 шкалы S
и т.д. (см. рис.I). В соответствии с этим
при появлении в выборке пары (I, I)
присваиваем
=
5, при появлении пары (2, 1) -
=2,
при появлении пар (3, 1), (4, 1), ..., (7, 1) -
=
5.
Аналогично при появлении пары (1, 2)
присваиваем
=
5, при появлении пары (2, 2) -
=
3, при появлении пары (3, 2) -
=
4, при появлении пар (4, 2), ..., (7, 2) -
=
5
и т.д. Все высказанное можно записать
следующими формулами.
Обозначим
=
,
(2)
-
целая часть X.
Как
и ранее, i принимает значения от I до n
,
j
– от I до n
.
Возможны два варианта: = 
и
.
I.
- целое ( = 
).
=
В
самом деле, легко видеть, что при целом
для
пропорциональных шкал j
–тому делению шкалы q
соответствует
делений шкалы S, а именно деления j,
j
- I, ... Поэтому
при появлении в выборке этих пар мы и
присваиваем
значение
+ I. Появление других пар свидетельствует
о непропорциональности, а потому
оценивается
I.
2.
- не целое (
=
).
89
Пусть
- элемент шкалы
,
соответствующийi-тому
значению шкалы S
и j-тому
значению шкалы q.
Доопределим
= 0 (
).Теперь
для
получим набор формул:
а)
при i
или i
n
+
1
,
=n
;
(4)
б)
при
i
=
+ 1 = i
,
=
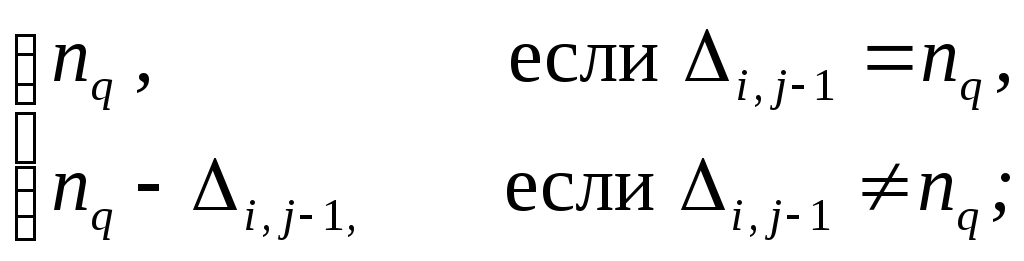(5)
в) при прочих значениях, обозначив
=
n
(
+
+ 2
i),
получим
=
(6)
Таблица I
-
i
I
2
3
4
5
6
7
j
I
5
2
5
5
5
5
5
2
5
3
4
5
5
5
5
3
5
5
I
5
I
5
5
4
5
5
5
5
4
3
5
5
5
5
5
5
5
2
5
90
Удостоверимся в этом. Здесь = 75, не целое:
I)
i
= 1, j = 1;
= 0; i = i
(случай
б);
=
=
0
n
.
Следовательно,
=
=
5
0 = 5;
2)
i = 2, j = 1;
(случай в);
=
5(
0 + 2
2) = 7;
=
=
5; ;
=
7
5 = 2
n
;
=
=
2;
3)
i = I, j = 2;
= 1 = i (случай
а);
=
=5;
4)
i = 2, j = 2;
(случай б).
=
=
2
n
;
=
=
5
2 = 3 и т.д.
Из
рассмотренных примеров ясно, как строится
шкала
и как работают формулы (3) – (6).
Построение шкалы
следует вести по строкам или столбцам,
начиная сi
= I, j
= I. Приведем еще два примера таблиц для
(табл. 2, 3):
I.
n
=
6, n
=
3.
Таблица 2
-
i
I
2
3
4
5
6
j
I
I
I
I
I
I
I
2
I
I
I
I
I
I
3
I
I
I
I
I
I
91
2.
n
=
7, n
=
4.
Таблица 3
-
i
I
2
3
4
5
6
7
j
I
4
3
4
4
4
4
4
2
4
I
4
2
4
4
4
3
4
4
4
2
4
I
4
4
4
4
4
4
4
3
4
Теперь,
как и в случае с ориентированием,
перебираем выборку N,
находим
и нормируем его, определяя коэффициент
пропорциональности шкал
=
=
.
(7)
Этот
метод, как уже было сказано выше, можно
использовать не только для проверки
пропорциональности, но и для
пропорционализации шкал. Процесс
пропорционализации состоит в том, чтобы,
дробя отдельные элементы одной из шкал
на несколько значений ( и тем увеличивая
её длину) или соединяя несколько элементов
шкалы в один ( и тем уменьшая её длину),
добиться наибольшего значения
. При
этом надо следить за социологическим
смыслом вновь получаемых шкал, чтобы
остановить процесс на некотором оптимуме
величины коэффициента связи.
Основная трудность состоит, вероятно, в формализации этого процесса и построении решающего алгоритма. Однако проблема эта еще автором до конца не решена, поскольку до сих пор не ясны критерии оптимизации процесса, учитывающие содержательную сторону пропорционализации.
92
Вопрос, затронутый в данной статье, важен еще и тем, что ориентировка и пропорционализация шкал позволяет решать задачи введения функциональных зависимостей на шкалах различных социологических признаков. Более того, поскольку для пропорциональных шкал такая зависимость будет линейного вида ax + b, можно будет задавать на множестве шкал те или иные алгебраические операции, моделирующие взаимовлияния рассматриваемых признаков.
93