лекции(II курс)

ЭЛЕМЕНТЫ ДИСКРЕТНОЙ МАТЕМАТИКИ. Тема 1. Основные понятия теории множеств.

1.1. Определения.

Определение. Множеством M называется объединение в единое целое определенных различимых объектов a, которые называются элементами множества. a M.

Определение. Если все элементы множества A являются также элементами множества B, то говорят, что множество A включается (содержится) в множестве B:

A B.

A

B

Определение. Два множества A è B считаем равными и пишем A = B, åñëè îíè

состоят из одних и тех же элементов, другими словами, если каждый элемент множества A является элементом множества B и наоборот.

Определение. Åñëè A B, то множество A называется подмножеством множества B, à åñëè ïðè ýòîì A ≠ B, то множество A называется собственным подмножеством множества B и обозначается A B.

Пустое множество обозначаю символом: .

Определение. Непустое множество называют конечным, если число его элементов

может быть выражено с помощью какого-либо целого положительного числа.

Например, множество всех решений в целых положительных числах уравнения x3 + y3 + z3 = 3 конечно (существует только одно такое решение x = y = z = 1).

1.2. Операции над множествами.

Определение. Объединением множеств A è B называется множество C, элементы которого принадлежат хотя бы одному из множеств A è B. Обозначается C = A B.

A B

Определение. Пересечением множеств A è B называется множество C, элементы которого принадлежат каждому из множеств A è B. Обозначение C = A ∩ B.

A

B

Определение. Разностью множеств A è B называется множество, состоящее из элементов множества A, не принадлежащих множеству B. Обозначается C = A \ B.

1

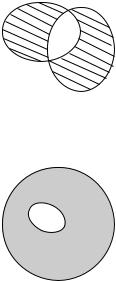
Определение. Симметрической разностью множеств A è B называется множество C, элементы которого принадлежат в точности одному из множеств A èëè B. Обозначается C = A B = (A \ B) (B \ A).

A

B

Определение. CE называется дополнением множества A относительно множества E, åñëè A E è CE = E \ A.

A

E

1.3. Декартово произведение множеств.

Напомним, что такое вектор.

Определение. Вектор это упорядоченный набор элементов или упорядоченное множество.

Элементы это координаты или компоненты вектора. Нумерация элементов производится слева направо.

Определение. Векторы {a1, a2}, {a1, a2, a3}, {a1, a2, a3, . . .} называют соответственно двойка, тройка, энка. Длина вектора количество элементов в векторе .

Определение. Два вектора {a1, a2, a3, . . . , an} è {b1, b2, . . . , bm} равны тогда и только тогда, когда n = m è a1 = b1, a2 = b2, . . . , an = bm.

Пример: {1, 2} = {1, 2}, íî {1, 2} ̸= {2, 1}.

Определение. Прямым (декартовым) произведением множеств A è B называют множество упорядоченных пар элементов: A × B = {(a, b) | a A, b B}.

Определение. Åñëè A = B, òî A × B = A2 и называется декартовым квадратом.

Определение. Пусть A1, A2, . . . , An какие -то непустые множества. Их декартовым произведением называется множество:

A1 × A2 × . . . × An = {{a1, a2, . . . , an} | a1 A1, a2 A2, . . . , an An}.

Определение. Åñëè A1 = A2 = . . . = An , òî A1 × A2 × . . . × An = An и называется декартовой степенью множества A.

2

Примеры:

1. R множество действительных чисел, тогда R × R = R2 векторы (a, b), ãäå a R è b R, есть координаты точек плоскости.

Такое координатное представление точек плоскости было предложено Рене Декартом

èявлялось первым в истории примером прямого (декартового) произведения множеств.

2.Прямое произведение {1, 2, 3, . . . , 8}×{a, b, c, d, . . . , h} есть множество клеток шах-

матной доски.

3. Рассмотрим множество A, элементы которого символы (буквы, цифры, знаки препинания, знаки операций и т.д.), тогда An это слова длиной n (под словом можно понимать

текст).

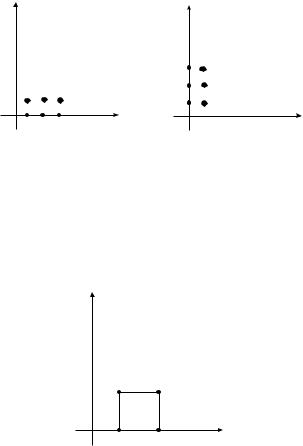
4. Составим прямое произведение множеств X = {1, 2, 3} è Y = {0, 1}:

X ×Y = (1, 0), (1, 1), (2, 0), (2, 1), (3, 0), (3, 1), Y ×X = (0, 1), (0, 2), (0, 3), (1, 1), (1, 2), (1, 3).

Геометрическая интерпретация произведения двух конечных множеств точки плоскости. Как видно из построенных произведений прямое произведение множеств не обладает свойством коммутативности.

5. Построим прямое произведение двух несчетных множеств числовых отрезков, например, [0, 1] × [1, 2]. Результатом данного произведения являются все точки квадрата с

вершинами (0, 1), (0, 2), (1, 1)(1, 2):

Y

Тема 2. Элементы математической логики. 2.1. Основные определения.

Математическая логика разновидность формальной логики, т.е. науки, которая

изучает умозаключения с точки зрения их формального строения.

Определение. Высказыванием называется предложение, к которому возможно применить понятия истинно или ложно.

В математической логике не рассматривается сам смысл высказываний, определяется только его истинность или ложность, что принято обозначать соответственно И или Л.

3

Понятно, что истинные и ложные высказывания образуют соответствующие множества. С помощью простых высказываний можно составлять более сложные, соединяя простые высказывания союзами "и "или". Таким образом, операции с высказываниями можно описывать с помощью некоторого математического аппарата.

Вводятся следующие логические операции (связки) над высказываниями

1) Отрицание. Отрицанием высказывания P называется высказывание, которое ис-

тинно только тогда, когда высказывание P ложно. Обозначается P .

Соответствие между высказываниями определяется таблицами истинности. В нашем случае эта таблица имеет вид:

2) Конъюнкция. Конъюнкцией двух высказываний P è Q называется высказывание, истинное тогда и только тогда, когда истинны оба высказывания. Обозначается Q.

3) Дизъюнкция. Дизъюнкцией двух высказываний P è Q называется высказывание, ложное тогда и только тогда, когда оба высказывания ложны. Обозначается P Q.

4) Импликация. Импликацией двух высказываний P è Q называется высказывание, истинное тогда и только тогда, когда высказывание P истинно, а Q ложно. Обозна- чается Q. Высказывание P называется посылкой импликации, а высказывание Q

5) Эквиваленция. Эквиваленцией двух высказываний P è Q называется высказыва-

ние, истинное тогда и только тогда, когда истинности высказываний совпадают. Обозна- чается P Q.

С помощью этих основных таблиц истинности можно составлять таблицы истинности сложных формул. Если в результате эти таблицы совпадают, то формулы эквивалентны.

4

Пример. С помощью таблиö истиннîсти проверить, являются ли эквивалентными формулы φ = p (p r) è ψ = p (p r).

Составим таблицы истинности для каждой формулы:

Данные формулы не являются эквивалентными.

Пример. С помощью таблиц истинности проверить, являются ли эквивалентными формулы φ = (p q) r è ψ = (p q) (q p) r.

2.2. Основные равносильности.

Для любых формул , и справåäливы следующие равносильности:

1.Закон двойного отрицания: A = A.

2.Идемпотентность операций и : A A = A, A A = A.

3.Коммутативность операций и : A B = B A, A B = B A.

4.Ассоциативность операций и : A (B C) = (A B) C, A (B C) = (A B) C.

5.Дистрибутивные законы каждой из операций и относительно другой:

A (B C) = (A B) (A C), A (B C) = (A B) (A C).

6.Законы поглощения: A (A B) = A, A (A B) = A

7.Законы де Моргана: A B = A B, A B = A B.

8. Свойство нуля A 0 = 0, A 0 = A.

10. Свойство единицы A 1 = A, A 1 = 1.

2.3. Булевы функции.

Определение. Булевой функцией f(X1, X2, . . . , Xn) называется называется произвольная n - местная функция, аргументы и значения которой принадлежат множеству {0, 1}.

Вообще говоря между логическими высказываниями, логическими связками и булевыми функциями просматривается явная аналогия. Если логические функции могут принимать значения истинно или ложно, то для булевой функции аналогами этих значений будут значения 0 или 1.

Для булевых функций также можно составить таблицы значений, соответствующим основным логическим операциям.

5

2.4. Исчисление предикатов.

Определение. Предикатом P (x1, x2, . . . , xn) называется функция, переменные которой принимают значения из некоторого множества M, а сама функция принимает два значения: И (истина) и Л (ложь), т.е.

P (x1, x2, . . . , xn) : Mn → {È, Ë}

Предикат от n аргументов называется n - местным предикатом. Высказывания счита-

ются нуль - местными предикатами. Над предикатами можно производить обычные логические операции, в результате которых получаются новые предикаты. Кроме обычных логических операций к предикатам применяются также специальные операции, называемые кванторами. Кванторы бывают двух видов:

1) Квантор общности. Обозначается ( x)P (x). Квантором общности называется высказывание истинное, когда P (x) истинно для каждого элемента x из множества M, è

ложное - в противном случае.

2) Квантор существования. Обозначается ( x)P (x). Квантором существования называется высказывание, истинное, когда существует элемент из множества M, для которого P (x) истинно, и ложное в противном случае.

Операцию связывания квантором можно применять и к предикатам от большего числа переменных.

Для формул логики предикатов сохраняется справедливость всех правил равносильных преобразований логики высказываний. Кроме того, справедливы следующие свой-

4) Переименование связанных переменных. Если заменить связанную переменную формулы A другой переменной, не входящей в эту формулу, в кванторе и всюду в области

действия квантора получаем формулу, равносильную A.

Исчисление предикатов базируется на приведенных выше свойствах и правилах, называемых аксиомами.

Какими бы ни были формулы А и В для них справедливы следующие аксиомы:

1)A (B A); 2)(A (B C)) ((A B) (A C));

3)(B A ((B A) B);

4)( xi)A(xi) A(xj), где формула A(xi) не содержит переменной xi.

5)A(xi) ( xj)A(xj), где формула A(xi) не содержит переменной xi.

6

Контрольные вопросы.

1.Понятие множества, отношение включение, равенство множеств.

2.Операции над множествами.

3.Декартово произведение множеств.

4.Математическая логика, как предмет. Понятие высказывания, виды и примеры высказываний.

5.Основные логические связки.

6.Основные равносильности.

7.Булевы функции.

8.Понятие предиката. Кванторы.

9.Свойства и аксиомы.

7

ТЕОРИЯ ВЕРОЯТНОСТЕЙ.

Тема 1. Предмет и основные понятия теории вероятностей. 1.1. Основные понятия теории вероятностей.

Одним из основных понятий теории вероятностей является понятие события.

Определение. Случайным событием(возможным событием или просто событием) называется любой факт, который в результате испытаний может произойти или не произойти.

Например: а) в Белгороде 1 сентября выпадут осадки, б) наудачу брошенная монета ляжет "орлом"и т.д.

Событие это не какое-нибудь происшествие, а лишь возможный исход, результат испытания (опыта, эксперимента).

События делятся на: достоверные; невозможные; случайные.

Определение. Достоверным называется событие, которое при заданном комплексе

условий обязательно произойдет.

Определение.Невозможным называется событие, которое при заданном комплексе

условий не может произойти.

Определение.Случайным называется событие, которое при заданном комплексе условий может произойти или не произойти.

Замечено, что случайные события в массовых испытаниях подчинены объективно существующим закономерностям. Предметом теории вероятностей является выявление этих

закономерностей.

Èòàê, теория вероятностей есть раздел математики, в котором изучаются только случайные явления (события) с устойчивой частостью и выявляются закономерности при массовом их повторении.

Виды случайных событий.

События обозначают заглавными буквами латинского алфавита: A,B,C и т.д.

1) События A и B называются несовместными если появление одного из них исклю- чает возможное появление другого.

Например, A выигрыш автомобиля по лотерейному билету, B выигрыш телевизора

по тому же лотерейному билету события несовместные.

2) События A и B называются совместными если появление одного не исключает появление другого.

Например, A выигрыш автомобиля по одному лотерейному билету, B выигрыш те-

левизора по другому лотерейному билету события совместные.

3) События A и B называются равновозможными если они имеют равную возможность появиться.

Например, извлечение туза, валета, короля или дамы из колоды карт либо появление герба или решки при подбрасывании монеты события равновозможные.

4)События A, B, C и т.д. образуют полную группу если они несовместны, равновозможны и в результàте испытания одно из них обязательно произойдет.

5)События A и A называются противоположными если они несовместны и образую

полную группу.

6) События A и B называются независимыми, если появление одного не связано с появлением другого.

Например, A поражение мишени 1 стрелком, B поражение мишени 2 стрелком.

8

7) События A и B называются зависимыми если появление одного зависит от появление другого.

A поражение одной мишени 1 стрелком, B поражение этой же мишени 2 стрелком, при условии непопадания 1-го стрелка.

1.2. Классическое определение вероятности.

Вероятность одно из основных понятий теории вероятностей. Существует несколько определений этого понятия. Приведем определение, которое называют классическим. Далее укажем слабые стороны этого определения и приведем другие определения, поз-

воляющие преодолеть недостатки классического определения.

Определение. Вероятностью появления события A называется отношение числа благоприятных этому событию исходов к общему числу всех единственно возможных и равномозможных исходов испытания.

ãäå m−число благоприятных исходов, n−общее число всех возможных исходов испыта-

íèÿ.

Вероятность численная мера появления события.

Пример. Монета подбрасывается два раза, найти вероятность того что хотя бы один раз появится орел.

Пусть A−выпал орел. Общее число всех возможных исходов n = 4, число благоприятных исходов m = 3. Таким образом: P (A) = 3/4.

Свойства вероятности.

1)Вероятность достоверного события равна 1.

2)Вероятность невозможного события равна 0.

3)Вероятность случайного события есть положительное число, заключенное между

нулем и единицей.

n0 < mn < nn, 0 < P (A) < 1.

Для успешного решения задач с использованием классического определения вероятности необходимо знать основные правила и формулы комбинаторики раздела математики, изучающего, в частости, методы решения комбинаторных задач задач на подсчет числа различных комбинаций.

1.3. Основные формулы комбинаторики.

Комбинаторика изучает количества комбинаций, подчиненных определенным условиям, которые можно составить из элементов, безразлично какой природы, заданного конечного множества.

Различные комбинации элементов множества называются выборками.

Выборки бывают трех видов: перестановки; размещения; сочетания.

Определение. Перестановками называют комбинации, состоящие из одних и тех же n различных элементов и отличающихся друг от друга только порядком их распо-

ложения.

9