ЛЕКЦИИ спецглавы высшей математики / ЛЕКЦИЯ_7_СГВМ / Функции Ганкеля

Фу́нкции Га́нкеля (Ха́нкеля) (Функции Бесселя третьего рода) - это линейные комбинации функций Бесселя первого и второго рода, а следовательно, решения уравнения Бесселя. Названы в честь немецкого математика Германа Ганкеля.

— функция Ганкеля первого рода;

— функция Ганкеля второго рода.

Функции Ганкеля с индексом 0 являются фундаментальными решениями уравнения Гельмгольца.

Свойства

• Представление функциями Бесселя первого рода:

• Определитель Вронского:

• Симметрия по индексу:

• Асимптотические представления:

, если ;

, если .

См. также

• Функции Бесселя

• Сферические функции

• Модифицированные функции Бесселя

Литература

• Ватсон Г., «Теория бесселевых функций» т. 1,2 М., ИЛ, 1949 г.

• Бейтмен Г., Эрдейи А. «Высшие трансцендентные функции. Функции Бесселя, функции параболического цилиндра, ортогональные многочлены». Справочная математическая библиотека М. Физматгиз 1966 г. 296 с.

ГАНКЕЛЯ ФУНКЦИИ,

Ханкеля функции,- цилиндрические функции3-го рода. Г. ф. могут быть следующим образом определены через Бесселя функции:

(р-нецелое). Отсюда вытекают важные соотношения

Г. ф. комплексны при действительныхзначениях z; однако

действительны, если z действительно и положительно. Г. ф. обладают простыми асимптотич. представлениями при больших |z|:

Г. ф. "полуцелого" аргумента выражаются через элементарные функции, в частности:

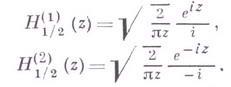
Г. ф. введена Г. Ганкелем (Н. Hankel, 1869).

Лит.:[1] Янне Е.,Эмде Ф., ЛешФ., Специальные функции. Формулы, графики, таблицы, 2 изд., пер. с нем., М., 1968. П. И. Лизоркин.

Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.