Вариант 7

1. Вектор , параллельный плоскости YOZ, составляет с осью OY угол 135. Найти координаты вектора , если.

2. Вектор коллинеарен вектору. Найти координаты вектора, если он удовлетворяет условию, где.

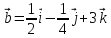3. Даны векторы и.Найти проекцию векторана вектор.

4. Даны вершины треугольника: А(2, 3, 1), В(4, 0, 3), С(1, 5, 1). Определить косинус угла между медианами ВМ и AN треугольника АВС.

5. Вектор , перпендикулярный векторами, образует с осьюOZ тупой угол. Найти его координаты, зная, что .

6. Найти длину высоты AD треугольника АВС, если ,.

7. Найти единичные векторы и, перпендикулярные векторами, если,.

8. Даны три силы , приложенные к точкеD(3, 5, 9). Вычислить работу, производимую равнодействующей этих сил, когда точка ее приложения, двигаясь прямолинейно, перемещается в точку Q(5, 6, 3).

9. Дана пирамида с вершинами в точках А( 9, 7, 4), В( 4, 3, 1), С(5, 4, 2), D(3, 4, 4). Найти ее объем и длину высоты, опущенной на грань BCD.

10. Определить, при каком значении  векторы , компланарны.

Вариант 8

1. Радиус-вектор точки М составляет с осью ОХ угол 120, а с осью ОZ угол 135; его длина равна 10. Найти координаты точки М, если ее ордината отрицательна.

2. Вектор , коллинеарный вектору, образует с осью ОZ тупой угол. Зная, что , найти его координаты.

3. Даны векторы ,. Найти проекцию векторана направление вектора.

4. Даны вершины треугольника АВС: А(2, 3, 0), В(1, 4, 1), С(5, 2, 3). Найти косинус угла между медианами АМ и СN.

5. Даны векторы , . Найти и , при которых вектор коллинеарен вектору.

6. Даны точки А(1, 2, 0), В(3, 0, 3), С(5, 2, 6). Вычислить площадь треугольника АВС и его высоту CD.

7. Найти вектор , ортогональный векторам ии удовлетворяющий условию, если.

8. Даны три силы , приложенные к точкеA(2, 4, 7). Вычислить работу, производимую равнодействующей этих сил, когда точка ее приложения, двигаясь прямолинейно, перемещается в точку B(0, 7, 4).

9. Дана пирамида с вершинами в точках А(4, 3, 1), В(2, 7, 5), С(4,2, 4), D(2, 3, 5). Найти ее объем и длину высоты, проведенной к грани АCD.

10. При каком значении λ вектор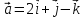ы , ,будут компланарны?

Вариант 9

1. Вектор коллинеарен вектору и удовлетворяет условию. Найти координаты вектора.

2. Вектор составляет с осями координат острые углы α, β, γ, причем α = 45,β = 60. Найти его координаты, если .

3. Даны векторы ,и. Найти проекцию векторана вектор.

4. Даны вершины четырехугольника А(1, 2, 2), В(1, 4, 0), С(4, 1, 1), D(5, 5, 3). Вычислить угол φ между его диагоналями.

5. Вектор , перпендикулярный векторам и, образует с оcью OZ тупой угол. Найти его координаты, если .

6. В треугольнике с вершинами А(1, 3, 1), В(2, 3, 4), С(3, 4, 4) найти высоту AD.

7. Найти единичный вектор, ортогональный векторам ии образующий с ортомострый угол.

8. Даны три силы , приложенные к точке С(3, 2, 0). Вычислить работу, производимую равнодействующей этих сил, когда точка ее приложения, двигаясь прямолинейно, перемещается в точку D(6, 4, 3).

9. Вершины пирамиды находятся в точках А(2, 3, 4), В(4, 7, 3), С(1, 2, 2) и D(2, 0, 1). Вычислить объем пирамиды и длину ее высоты, опущенной из вершины А на грань BCD.

10. Определить, при каком значении λ векторы , ,будут компланарны.