Лекции 01-16

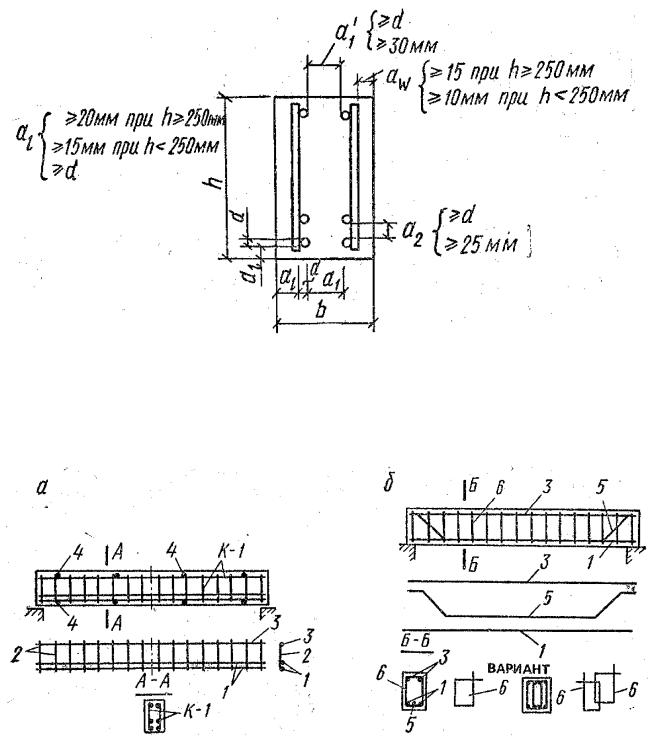
3

арматурных стержней можно не доводить до опор и обрывать в пролете там, где они по расчету на восприятие изгибающего, момента не требуются. Площадь сечения продольной рабочей арматуры As в изгибаемых элементах должна определяться расчетом, но составлять не менееμ=0,05 % площади сечения элемента с размерами b и ho. Для продольного армирования балок обычно применяют стержни периодического профиля (реже гладкие) 12...32 мм.

Рис.1.3.4.Размещение арматуры в поперечном сечении балок: аL-

защитный слой бетона для рабочей арматуры; аw- то же для поперечной арматуры; d- наибольший диаметр рабочих стержней; а1- расстояние в свету между нижними (при бетонировании) продольными стержнями; а1-то же, между верхними (при бетонировании) стержнями; а2- расстояние в свету между рядами продольных стержней.

Рис.1.3.5.Схемы армирования балок сварными каркасами (а) и

вязаной арматурой (б): 1 - продольные рабочие стержни (стержни второго ряда не доведены до опор); 2 - поперечные стержни каркасов; 3- продольные

4

монтажные стержни; 4- поперечные соединительные стержни; 5- рабочие стержни с отгибами; 6- хомуты вязаных каркасов.

Вбалках шириной 150 мм и более предусматривают не менее двух продольных (доводимых до опоры) стержней; при ширине менее 150 мм допускается установка одного стержня (одного каркаса).

Вжелезобетонных балках одновременно с изгибающими моментами действуют, поперечные силы, что вызывает необходимость устройства поперечной арматуры. Количество ее определяют по расчетам и конструктивным требованиям.

При армировании вязаными каркасами (рис.1.3.5, б) хомуты в балках прямоугольного сечения делают замкнутыми; в тавровых балках, в которых ребро сечения с обеих сторон связано с монолитной плитой, хомуты могут быть скрытые сверху. В балках шириной более 350 мм устанавливают многоветвевые хомуты. Диаметр хомутов вязаных каркасов принимают не менее 6 мм при высоте балок до 800 мм и не менее 8 мм при большей высоте.

По расчетно-конструктивным условиям расстояние в продольном направлении между поперечными стержнями (или хомутами) в элементах без отгибов должно быть: в балках высотой до 400 ммне более h/2, но не более 150 мм; в балках высотой выше 400 мм - не более h/3, но не более 500 мм. Это требование относится к приопорным участкам балок длиной l/4 пролета элемента при равномерно распределенной нагрузке, а при сосредоточенных нагрузках, кроме того, и на протяжении от опоры до ближайшего груза, но не менее 1/4 пролета. В остальной части элемента расстояние между поперечными стержнями (хомутами) может быть больше, но не более чем 3/4 h и не более 500 мм.

Поперечные стержни (хомуты) в балках и ребрах высотой более 150 мм, ставят, даже если они не требуются по расчету; при высоте менее 150 мм поперечную арматуру можно не применять, если удовлетворяются требования расчета.

При армировании балок вязаными каркасами для экономии стали и улучшения конструкции каркаса целесообразно устройство отгибов части продольных рабочих стержней (см. рис. 1.3.5 б). Закругления отгибов выполняют по дуге с радиусом не менее 10d. Отгибы оканчиваются прямыми участками длиной не менее 0,8 lan и не менее 20d в растянутой или 10d в сжатой зоне. Прямые участки отгибов из гладких стержней оканчиваются крюками.

5

1.3.2. Расчет прочности по нормальным сечениям изгибаемых элементов с одиночной арматурой.

Элементы прямоугольного сечения с одиночной арматурой. Для прямоугольных сечений с одиночной ненапрягаемой арматурой (см. рис.1.3.5) расчетные формулы прочности нормальных сечений получают путем подстановки в них геометрических характеристик прямоугольных сечений:

Рис.1.3.5.схема напряжений и усилий в нормальном расчетном сечении; 1- нормальное сечение.

При ΣМ=0 относительно оси, проходя щей через центр тяжести бетона сжатой зоны сечения, имеем

Основные уравнения прочности прямоугольных сечений изгибаемых элементов (3.3-3.5) справедливы при высоте сжатой зоны х меньше граничной высоты xR, т.е. когда соблюдается условие x≤ξRh0, где ξR определяют по выражению ξR=xR/h0

Формулы (3.4) и (3.5) показывают, что при одной и той же несущей способности элемента сечение арматуры получается тем меньше, чем больше

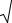
6

плечо внутренней пары сил Zb = hо - 0,5х, т. е. чем больше рабочая высота сечения hо. Следовательно, можно получить. сечения элементов с большим и меньшим содержанием арматуры. Примерные оптимальные проценты армирования приведены выше.

В целях упрощения расчетов по подбору размеров нормальных сечений изгибаемых элементов и площади сечения и рабочей арматуры рекомендуется пользоваться коэффициентами αm и ζ, вычисленными в зависимости от относительной высоты сжатой зоны ξ. Коэффициент αm позволяет основное уравнение прочности (3.4) записать в таком виде:

Если αm≤ αR =ξR(1-0,5ξR), то сжатая арматура не требуется. Коэффициент ζ; позволяет уравнение прочности (3.5) записать в виде:

где:

ζ=(ho-0,5х)/ho=1-0,5x/ho=1-0,5ξ (3.10)

Сечение растянутой арматуры Аs может быть определено из формулы (3.3), подставив в нее значение х=ho;

нли по проценту армирования μ с учетом формулы ξ=μRs/(100Rb) получаемую из выражений минимального процента армирования:

Для уменьшения ширины раскрытия трещин диаметр продольной рабочей арматуры рекомендуется принимать минимально возможным из условия размещения арматурных стержней (канатов) в один ряд по ширине балки, но не менее 12 мм. Защитный слой арматуры аь принимают минимальным в целях максимально возможного увеличения рабочей высоты сечения h0.

7

С помощью таблиц легко можно решать три типа задач при подборе и проверке прочности нормальных прямоугольных сечений.

Задача 1.Опредеклить площадь сечения арматуры Аs по заданным ho,b,Rb,Rs,M. (прямая задача):

Решение: По формуле ξR=xR/h0 определяют граничную относительную высоту бетона сжатой зоны сечения ξ. По формуле (3.6.) определяют коэффициент αm, по которому по средствам приложения находят коэффициент ξ

и ζ. Проверяют условия нормального армирования элементов ξ≤ξR если окажется что ξ>ξR, то размеры заданного сечения при данном классе бетона не достаточны. Необходимо на основании технико экономического сравнения увеличить на модуль, равный 50мм, высоты h или b ширину сечения, или на одну ступень повы сить класс бетона. Если ξ≤ξR то по формуле (3.9) определяют искомую площадь продольной арматуры.

Задача 2.Определить рабочую высоту элемента ho по заданным μ,b,Rb,Rs,M. (обратная задача).

Решение: По формуле ξR=xR/h0 определяют граничную относительную

высоту бетона сжатой зоны сечения ξ. По, формуле ξ=μRs/(100Rb) находят ξ. Если окажется что ξ>ξR, то поступают так же, как в задаче 1. При ξ≤ξR по значению коэффициента ξ находят коэффициент αm и по формуле (3.7.) - искомую рабочую высоту элемента ho.

Если продет армирования μ не задан, то его принимают средним по табл.В практике задаются оптимальным коэффициентом ξopt; последующий ход решения остается прежним.

Задача 3. Проверить прочность сечения по известным Аs,b,h,M,Rь и Rs. Решение: По формуле ξR=xR/h0 определяют граничную относительную высоту

бетона сжатой зоны сечения ξ. При ξ≤ξR сечение переармированно. Если ξ>ξR значению коэффициента ξ находят коэффициент αm; коэффициентом αm по формуле (3.6)определяют несущую способность сечения Mu. Полученное значение Mu должно быть не меньше заданного: M≤ Mu.

Табличный способ расчета.

Проверку прочности прямоугольных сечений с одиночной арматурой производят:

при х < ξRho из условия:

M ≤ RsAs (h0-0, 5x) (3.13)(пос. фор.3.20.)

где х - высота сжатой зоны, равная x = Rs As ; ξR –(см. пос.п.3.17)

Rbb

при х ≥ ξRho из условия:

где aR –( см.пос. табл. 3.2) при этом несущую способность можно несколько увеличить, используя рекомендацию (фор.3.19.)

Подбор продольной арматуры производят следующим образом: Вычисляют значение:

αm = M 2

Rbbh0 (3.15)(пос. фор.3.22.)

Если aт < aR (см.пос.табл. 3.2), сжатая арматура по расчету не требуется. При отсутствии сжатой арматуры площадь сечения растянутой арматуры определяется по формуле

Если aт > aR , требуется увеличить сечение или повысить класс бетона, или установить сжатую арматуру согласно (пос.п.3.22.).

1.3.3. Расчет элементов прямоугольного, таврового, двутаврового профиля, элементы

с двойным армированием.

Прямоугольные сечения.

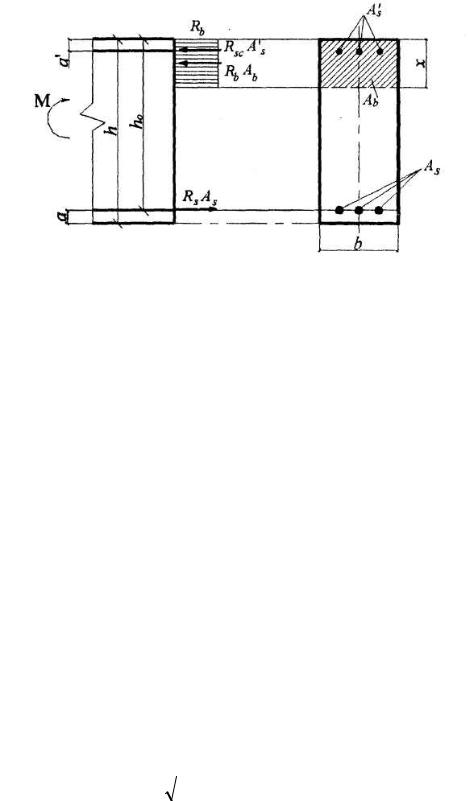
Расчет прямоугольных сечений (рис.1.3.6.) производится следующим образом в зависимости от высоты сжатой зоны:

а) при ξ = hx0 ≤ ξR - из условия:

где αR = ξR (1−0,5ξR ) или (см.пос. табл. 3.2.)

Правую часть условия (3.15) при необходимости можно несколько увеличить путем замены значения aR на (0,7 aR + 0,3 am), где am = ξ(1 - 0,5 ξ), и принимая здесь ξ не более 1.

Рис.1.3.6.Схема усилий и эпюра напряжений в поперечном прямоугольном сечении изгибаемого железобетонного элемента.

Если вычисленная без учета сжатой арматуры (As= 0,0) высота сжатой зоны х меньше 2а', проверяется условие (3.16), где вместо а' подставляется х/2.

Изгибаемые элементы рекомендуется проектировать так, чтобы обеспечить выполнение условия ξ ≤ ξR . Невыполнение этого условия можно

допустить лишь в случаях, когда площадь сечения растянутой арматуры определена из расчета по предельным состояниям второй группы или принята по конструктивным соображениям.

Площади сечения растянутой As и сжатой A's арматуры, соответствующие минимуму их суммы, если по расчету требуется сжатая арматура (см.пос.п.3.21), определяют по формулам:

где ξR и aR (см.пос.табл. 3.2)

Если значение принятой площади сечения сжатой арматуры As

значительно превышает значение, вычисленное по формуле (3.21), площадь сечения растянутой арматуры можно несколько уменьшить по сравнению с вычисленной по формуле (3.22), используя формулу

При этом должно выполняться условие aт < aR (см.пос.табл. 3.2).

10

Тавровые и двутавровые сечения.

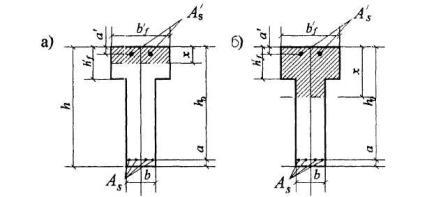
Расчет сечений, имеющих полку в сжатой зоне (тавровых, двутавровых и т.п.), производят в зависимости от положения границы сжатой зоны:

а) если граница проходит в полке (рис.1.3.6.а), т.е. соблюдается условие

расчет производят как для прямоугольного сечения шириной b'f ;

б) если граница проходит в ребре (рис.1.3.6.б.), т.е. условие (3.24) не соблюдается, расчет производят из условия:

Рис.1.3.6.Положение границы сжатой зоны в тавровом сечении изгибаемого железобетонного элемента. а-в палке; б - в ребре

.

M ≤ Rbbx(h0 −0,5x)+ Rb A0v (h0 −0,5h'f )+ Rsc As' (h0 − a' )(3.24)(пос. фор.3.28.)

где А0v - площадь сечения свесов полки, равная (b'f -b)h'f, при этом высоту сжатой зоны определяют по формуле:

и принимают не более ξRho (см.пос.табл. 3.2).

Если х> ξRho условие (3.28) можно записать в виде

M ≤ aR Rbbh02 + Rb A0v (h0 −0,5h'f )+ Rsc As' (h0 − a' )(3.26)(пос. фор.3.30.)

где aR – (см.пос.табл. 3.2).

При переменной высоте свесов полки допускается принимать значение h'f равным средней высоте свесов. Ширина сжатой полки b'f, вводимая в расчет, не должна превышать величин, указанных:

Значение b'f вводимое в расчет, принимают из условия, что ширина свеса полки в каждую сторону от ребра должна быть не более 1/6 пролета элемента и не более:

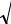
11

а) при наличии поперечных ребер или при h'f ≥ 0,1h - 1/2 расстояния в свету между продольными ребрами;

б) при отсутствии поперечных ребер (или при расстояниях между ними, больших, чем расстояния между продольными ребрами) и при h'f < 0,1h -

6h'f ;

в) при консольных свесах полки:

ξRho, площадь сечения сжатой арматуры определяют как для прямоугольного сечения шириной b = b'f по формуле (3.21).

Требуемую площадь сечения растянутой арматуры определяют следующим образом:

а) если граница сжатой зоны проходит в полке, т.е. соблюдается

условие:

M ≤ Rbb'f h'f (h0 −0,5h'f )+ Rsc As' (h0 − a' )(3.28)(пос. фор.3.32.)

площадь сечения растянутой арматуры определяют как для прямоугольного сечения шириной b'f согласно фор.3.16 и 3.23;

б) если граница сжатой зоны проходит в ребре, т.е. условие (3.28) не соблюдается, площадь сечения растянутой арматуры определяют по формуле

При этом должно выполняться условие aт ≤ aR (см.пос.табл. 3.2).

1

Лекция №6.

1.3.4. Особенности предельного состояния наклонного сечения изгибаемых элементов

На приопорных участках изгибаемых элементов под воздействием поперечной силы Q и изгибающего момента М в сечениях, наклонных к оси, развивается напряженно-деформированное состояние, характеризующееся теми же тремя стадиями, что и в сечениях, нормальных к оси. Главные растягивающие и главные сжимающие напряжения, возникающие при плоском напряженном состоянии под влиянием нормальных и касательных напряжений, действуют под углом к оси (рис. 1.3.7). Если главные растягивающие напряжения σmt превысят сопротивление бетона растяжению Rbt, возникают наклонные трещины; тогда усилия передаются на арматуру продольную, поперечную и, в общем случае возможную, отогнутую.

Рис.1.3.7.Главные напряжения в бетоне у опоры балки.

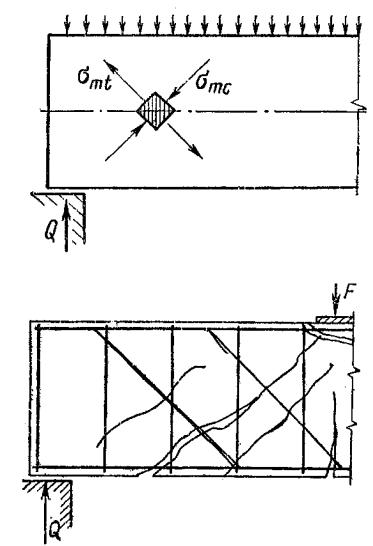
Рис.1.3.8.Разрушение балки по наклонному сечению.

При дальнейшем увеличении нагрузки наклонные трещины раскрываются и в конечной стадии происходит разрушение элемента вследствие