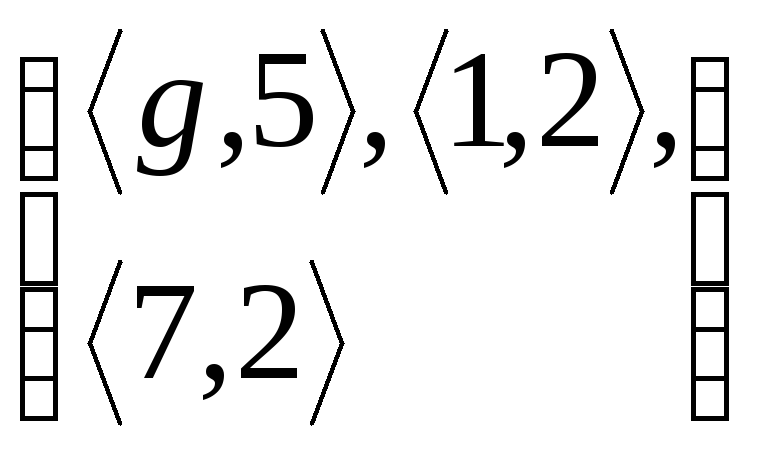- •Лабораторная работа 1 Основы теории множеств
- •Лабораторная работа 2 Множества, задание множества с помощью предиката
- •Лабораторная работа 3 Функции и операции над ними
- •Индивидуальные задания 2
- •Индивидуальные задания 3
- •Индивидуальные задания 4
- •Лабораторная работа 4 Перестановки, нумерующие биекции
- •Лабораторная работа 5 Изучение множеств с помощью их числовых кодов
- •Индивидуальные задания
- •Индивидуальные задания
- •Лабораторная работа 6 Формула включений и исключений
- •Лабораторная работа 7 Элементы комбинаторики
Лабораторная работа 3 Функции и операции над ними
Цель работы
Целью лабораторной работы является изучение понятия функции и получение навыков решения типовых задач с использованием функций
Краткие теоретические положения
Упорядоченная пара объектов
Пусть
даны множества
![]() и
и![]() .
Упорядоченной парой
.
Упорядоченной парой![]() иликортежем
двух
неравных объектов
иликортежем
двух
неравных объектов
![]() с компонентами
с компонентами
![]() и
и![]() называется величина
называется величина![]() ,
то есть двухэлементное множество,
состоящее из одноэлементного
множества синглета
,
то есть двухэлементное множество,
состоящее из одноэлементного
множества синглета
![]() ,
содержащегопервый
элемент пары
– объект а,
и двухэлементного множества
,
содержащегопервый
элемент пары
– объект а,
и двухэлементного множества
![]() ,то
есть неупорядоченной пары, отражающей
состав кортежа. Объект
,то
есть неупорядоченной пары, отражающей
состав кортежа. Объект
![]() называетсявторой
компонентой
кортежа. Если объекты
называетсявторой
компонентой
кортежа. Если объекты
![]() и
и![]() совпадают, то есть выполняется соотношение
тождественности
совпадают, то есть выполняется соотношение
тождественности![]() ,
то по определению
,
то по определению![]() .
В этом случае по определению первая и
вторая компонента кортежа совпадает с
указанным единственным объектом
.
В этом случае по определению первая и
вторая компонента кортежа совпадает с
указанным единственным объектом![]() .
.
Теорема 1.
(Критерий равенства двух кортежей). Для
кортежей имеет место равенство
![]() в том и только том случае, если выполняется
система двух равенств:
в том и только том случае, если выполняется
система двух равенств: .
.
Доказательство. Нужно различать два случая.
Случай
первый
![]() .
В этом случае
.
В этом случае![]() и при
и при![]() мы имеем равенство
мы имеем равенство![]() ,
которое невозможно, так как множество
,
которое невозможно, так как множество
![]() состоит только
из одного объекта – синглета
состоит только
из одного объекта – синглета
![]() ,
а множество
,
а множество![]() содержит также двухэлементное множество
содержит также двухэлементное множество![]() .
Поэтому имеет место равенство
.
Поэтому имеет место равенство![]() и
и![]() .
Получаем равенство
.
Получаем равенство![]() ,
откуда следует, что
,
откуда следует, что![]() .
.
Таким
образом, в указанном частном случае
имеем
 то
есть указанная система выполняется.
то
есть указанная система выполняется.
Рассмотрим
второй частный случай
![]() и равенство
и равенство![]() .
В случае
.
В случае![]() оно невозможно, как установлено перед
этим. Поэтому
оно невозможно, как установлено перед
этим. Поэтому![]() ,
,![]() и мы получаем равенство
и мы получаем равенство
![]() .
В этом равенстве синглеты и пары должны
совпадать, отсюда имеем
.
В этом равенстве синглеты и пары должны
совпадать, отсюда имеем
 ,
что равносильно данной системе
,
что равносильно данной системе .
.
Теорема доказана.
Декартово произведение двух множеств
Пусть
даны два множества
![]() и
и![]() .
Декартовым произведением
.
Декартовым произведением![]() первого множества на второе называется
множество всех упорядоченных пар
первого множества на второе называется
множество всех упорядоченных пар![]() ,
где
,
где![]() и
и![]() ,
то есть
,
то есть![]() .
.
Пример 2.1.
Дано
![]() .
Найти декартово произведение
.
Найти декартово произведение![]() ,
а также множество
,
а также множество![]() ,
изобразить эти множества на целочисленной
решетке
,
изобразить эти множества на целочисленной
решетке![]() .
.
Решение. Имеем
![]() .
.
Изобразим данное множество:

![]()
Изобразим данное множество на целочисленной решетке:

Функция
Пусть
даны
два множества
![]() и
и![]() .
Функцией из множества
.
Функцией из множества![]() в множествоВ
называется подмножество
в множествоВ
называется подмножество
![]() декартового произведения множеств
декартового произведения множеств![]() и
и![]() ,
обладающее свойством
,
обладающее свойством![]() .
Данное свойство называетсяфункциональным
свойством
и означает, что для каждого значения
аргумента
.
Данное свойство называетсяфункциональным
свойством
и означает, что для каждого значения
аргумента
![]() функция сопоставляет не более одного
значения
функция сопоставляет не более одного
значения![]() .
.
Пример 2.2.
Дано
![]() начальное
и конечное множества функции,
начальное
и конечное множества функции,![]() функция
из
функция
из
![]() в
в![]() .
Найти значение функции
.
Найти значение функции![]() .
.
Решение.
Поиск: Ищем пару вида
 .
Результат этапа 1:Такая пара найдена и
притом только одна
.
Результат этапа 1:Такая пара найдена и
притом только одна ;
;Выборка: Из найденной пары извлекаем второй элемент, этот элемент будет искомым значением функции
 .
Таким образом, получаем
.
Таким образом, получаем .
.
Ответ:
![]() .
.
Изобразить
данную функцию на решетке
![]() .
.
Решение.

Область определения и область значений функции
Пусть
дана функция
![]() из
множества
из
множества![]() в множество
в множество![]() .Область
определения
данной функции это
множество
.Область
определения
данной функции это
множество
![]() .Область
значений
функции
.Область
значений
функции
![]() это
множество
это
множество
![]() .
То есть область определения функции – это
множество первых компонент кортежей,
входящих в состав функции, а область
значений – это множество вторых
компонент.
.
То есть область определения функции – это
множество первых компонент кортежей,
входящих в состав функции, а область
значений – это множество вторых
компонент.
Пример 2.3.
Дано
![]() .
Найти
.
Найти![]() .
.
Решение.
Путем анализа исходных данных сразу
получаем ответ
![]() .
.
Образ множества, прообраз множества, прообраз элемента при действии функции
Пусть
дана функция
![]() и подмножество
и подмножество![]() .Образом
.Образом
![]() подмножества
подмножества![]() при действии функции
при действии функции![]()
![]() называется множество
называется множество![]() .
То есть образ подмножества
.
То есть образ подмножества![]() при действии функции
при действии функции![]() этомножество
вторых компонент кортежей
функции,
когда первые компоненты берутся из
подмножества
этомножество
вторых компонент кортежей
функции,
когда первые компоненты берутся из
подмножества
![]() .
Пусть
.
Пусть![]()
подмножество конечного множества
функции
подмножество конечного множества
функции
![]() .
Егопрообразом
.
Егопрообразом
![]() при действии функции
при действии функции![]() называется множество
называется множество![]() .
То есть прообраз подмножества
.
То есть прообраз подмножества![]() при действии функции
при действии функции![]() этомножество
первых компонент кортежей
функции,
когда вторые компоненты берутся из
подмножества
этомножество
первых компонент кортежей
функции,
когда вторые компоненты берутся из
подмножества
![]() .
.
Пусть
дан элемент
![]() его прообразом
его прообразом![]() при действии функции
при действии функции![]() называется множество
называется множество![]() ,
то есть прообраз одноэлементного
множества
,
то есть прообраз одноэлементного
множества![]() при действии функции
при действии функции![]() .
.
Пример 2.4. Дано
![]() ,
,
![]() .
Найти
.
Найти
![]() .
.
Решение.
Исходя из определения и данного состава
функции ![]() непосредственно выписываем ответ:
непосредственно выписываем ответ:
![]() .
.
Композиция и джойн функций
Пусть
даны две функции
![]() и
и![]() ихкомпозицией
ихкомпозицией
![]() называется функция
называется функция![]() вида
вида![]() .
Это определение можно пояснить следующей
схематической диаграммой
.
Это определение можно пояснить следующей
схематической диаграммой

Таким
образом, при композиции
![]() первой выполняется функция
первой выполняется функция![]() ,
то есть первая справа. Имеют место
следующие соотношения
,
то есть первая справа. Имеют место
следующие соотношения![]() ,
,
![]() .
.
Композиция
![]() функций
функций![]() и
и![]() может быть записана в видеджойна
этих функций
может быть записана в видеджойна
этих функций
![]() ,
,
где
![]() операция
джойна (то есть операция соединения или
конкатенации).
операция
джойна (то есть операция соединения или
конкатенации).
Таким образом, при операции джойна первой выполняется функция первая слева.
Пример 2.5.
Даны
функции
![]() ,
где универсум
,
где универсум![]() и
и![]() .
Построить композиции и джойны
.
Построить композиции и джойны![]() ,
выписать их кортежный состав и табличное
представление.
,
выписать их кортежный состав и табличное
представление.
Решение. Получим сначала табличное представление этих функций.
Имеем:
![]() ,
,
|
|
|
|
|
|
|
|
|
|
![]()
|
|
3 |
4 |
|
|
3 |
|
Находим
![]() .
Имеем:
.
Имеем:![]() .
.
Находим
значения функции
![]() на всех элементах ее области определения.
Имеем:
на всех элементах ее области определения.
Имеем:
![]() ,
,
![]() .
.
Таким образом, получили ответ по первой части задачи:
![]() ,
,
|
|
2 |
3 |
|
|
4 |
3 |
Из
табличного получаем кортежное
представление
![]() .
Так как
.
Так как![]() ,
автоматически получаем:
,
автоматически получаем:
![]() ,
,
|
|
2 |
3 |
|
|
4 |
3 |
![]() .
.
Таким же способом находим ответ для второй части задачи.
![]() ,
,
![]() .
.
То
есть,
![]()
|
|
3 |
|
|
3 |
и
![]() .
.
Для соответствующего джойна ответ получаем автоматически:
![]()
|
|
3 |
|
|
3 |
![]() .
.
Отображения. Инъекция, сюръекция, биекция, свойства обратимости слева и справа
Функция
![]() для которой
для которой![]() называетсявсюду
определенной,
обозначается
называетсявсюду
определенной,
обозначается
![]() или
или![]() и называется такжеотображением.
и называется такжеотображением.
Тождественным
отображением
![]() на множестве
на множестве![]() называется отображение
называется отображение![]() ,
обладающее свойством
,
обладающее свойством![]() ,
то есть это отображение оставляет каждый
элемент области определения на месте.
,
то есть это отображение оставляет каждый
элемент области определения на месте.
Пусть
![]() функция
и
функция
и
![]() подмножество
ее области определения. Сужением
подмножество
ее области определения. Сужением
![]() функции на множество
функции на множество![]() называется функция
называется функция![]() .
Эта функция является отображением вида
.
Эта функция является отображением вида![]() .
Имеет место формула:
.
Имеет место формула:![]() .
.
Пример 2.6. Дано
![]() .
.
Найти
сужение
![]() .
.
Решение. Имеем:

Ответ:
![]() .
.
Функция
![]() называетсяпродолжением
функции
называетсяпродолжением
функции
![]() ,
если выполняется включение
,
если выполняется включение![]() .
.
Отображение
![]() называетсясюръективным
или
сюръекцией
(отображением
«на», накрытием) если
называетсясюръективным
или
сюръекцией
(отображением
«на», накрытием) если
![]() ,
то есть если его образ совпадает со всем
конечным множеством отображения. Это
условие можно записать также в виде:
,
то есть если его образ совпадает со всем
конечным множеством отображения. Это
условие можно записать также в виде:![]() ,
то есть каждый элемент конечного
множества является образом некоторого
элемента начального множества отображения.
,
то есть каждый элемент конечного
множества является образом некоторого
элемента начального множества отображения.
Отображение
![]() называетсяинъективным
или
инъекцией,
если выполняется свойство
называетсяинъективным
или
инъекцией,
если выполняется свойство
![]() ,
то есть разные переходят в разные.
,
то есть разные переходят в разные.
Отображение
![]() называется
биективным
или биекцией
(взаимно-однозначным
отображением, перестановкой) если оно
одновременно сюръекция и инъекция.
называется
биективным
или биекцией
(взаимно-однозначным
отображением, перестановкой) если оно
одновременно сюръекция и инъекция.
Пусть
дано отображение
![]() .
Отображение
.
Отображение![]() называетсялевым
обратным к
отображению
называетсялевым
обратным к
отображению
![]() если выполняется свойство
если выполняется свойство![]() .
Отображение
.
Отображение![]() называетсяправым
обратным
к
называетсяправым
обратным
к
![]() ,
если
,
если![]() .
Отображение
.
Отображение![]() называетсяобратным
к отображению
называетсяобратным
к отображению
![]() ,
если оно одновременно является правым
обратным и левым обратным по отношению
к
,
если оно одновременно является правым
обратным и левым обратным по отношению
к![]() ,
то есть если выполняются свойства
,
то есть если выполняются свойства![]() .
.
Теорема 2.
Пусть имеется отображение
![]() .
Оно обладает левым обратным
.
Оно обладает левым обратным![]() тогда и только тогда, когда отображение
тогда и только тогда, когда отображение![]() является инъекцией. При этом левое
обратное находится по формуле:
является инъекцией. При этом левое
обратное находится по формуле:
Отображение
![]() обладает правым обратным
обладает правым обратным![]() ,
если
,
если![]() является
сюръекцией, при этом обратное
является
сюръекцией, при этом обратное![]() находится по формуле:
находится по формуле:
Отображение
![]() обладает как левым обратным
обладает как левым обратным![]() ,
так и правым обратным
,
так и правым обратным![]() в том и только том случае, если
в том и только том случае, если![]() биекция.
В этом случае левое и правое обратные
отображения совпадают, определяются
однозначно и их общее значение называется
обратным (двусторонним) отображением
биекция.
В этом случае левое и правое обратные
отображения совпадают, определяются
однозначно и их общее значение называется
обратным (двусторонним) отображением
![]() к отображению
к отображению![]() .
.
Задание функции программой ЭВМ
Пример
2.7. Функция
![]() заданаC++
программой:
заданаC++
программой:
int f(int x)
{
if (x>5) return x*2;
else if (3<=x) return (x/2);
else return x%2;
}
Найти
значение
![]() .
.
Решение. Для большей ясности действия указанной функции построим схему алгоритма данной функции:

Используя
входные данные
![]() осуществим прохождение от точки входа
то точки выхода блок-схемы.
осуществим прохождение от точки входа
то точки выхода блок-схемы.
1)
![]() вход
в схему;
вход
в схему;
2.Безусловный 1 переход на блок 2;
3)
Проверка
![]() нет,
переход по дуге 2 на блок 3;
нет,
переход по дуге 2 на блок 3;
4)
Проверка
![]() нет,
переход по дуге на исполнительный блок
5;
нет,
переход по дуге на исполнительный блок
5;
5)
Операция
![]() .
Результат
.
Результат![]() :
:
6) Безусловный переход на блок 7:
7)
Вывод данных
![]() .
.
Итак,
выполняя алгоритм данной функции по
указанной схеме алгоритма получили
ответ
![]() .
.
Задание
Выполнить задания 14, записать решения, ответить на контрольные вопросы.
Задание
1.
Кортежное задание функции.
Даны начальное и конечные множества
![]() ,
функция
,
функция![]() ,
найти область определения
,
найти область определения![]() ,
область значений
,
область значений![]() функции, получить табличное представление
функции. Привести визуальное изображение
функции в виде двудольного орграфа.
функции, получить табличное представление
функции. Привести визуальное изображение
функции в виде двудольного орграфа.
Пример выполнения.
Дано
![]() .
.
Решение.
Область определения функции - это
множество первых компонент ее кортежей.
Получаем
![]() .
Область значений это
множество вторых координат ее кортежей.
Получаем
.
Область значений это
множество вторых координат ее кортежей.
Получаем
![]() .
Табличное представление функции это
таблица аргумент-значение для всех
элементов области определения функции.
Получаем таблицу:
.
Табличное представление функции это
таблица аргумент-значение для всех
элементов области определения функции.
Получаем таблицу:
|
|
2 |
3 |
4 |
|
|
|
|
|
Изображение:

Индивидуальные задания 1.
|
№ вар |
|
|
|
№ вар |
|
|
|
|
1 |
|
|
|
2 |
|
|
|
|
3 |
|
|
|
4 |
|
|
|
|
5 |
|
|
|
6 |
|
|
|
|
7 |
|
|
|
8 |
|
|
|
|
9 |
|
|
|
10 |
|
|
|
|
11 |
|
|
|
12 |
|
|
|
|
13 |
|
|
|
14 |
|
|
|
|
15 |
|
|
|
16 |
|
|
|
|
17 |
|
|
|
18 |
|
|
|
|
19 |
|
|
|
20 |
|
|
|
|
21 |
|
|
|
22 |
|
|
|
|
23 |
|
|
|
24 |
|
|
|
|
25 |
|
|
|
26 |
|
|
|
|
27 |
|
|
|
28 |
|
|
|
|
29 |
|
|
|
30 |
|
|
|
|
31 |
|
|
|
32 |
|
|
|
|
33 |
|
|
|
34 |
|
|
|
|
35 |
|
|
|
36 |
|
|
|
|
37 |
|
|
|
38 |
|
|
|
|
39 |
|
|
|
40 |
|
|
|
Задание
2.
Образ множества, прообраз множества,
прообраз элемента. Дано:
Множества
![]() ,
функция
,
функция![]() ,
подмножество
,
подмножество![]() ,
подмножество
,
подмножество![]() ,
элемент
,
элемент![]() .
Найти: Образ подмножества
.
Найти: Образ подмножества![]() ,
то есть подмножество
,
то есть подмножество![]() ,
прообраз подмножества
,
прообраз подмножества![]() ,
то есть множество
,
то есть множество![]() ,
прообраз элемента
,
прообраз элемента![]() ,
то есть подмножество
,
то есть подмножество![]() .
.
Пример выполнения. Дано:

Найти объекты, указанные в задании.
Решение. Используем графическую интерпретацию функции как двудольного орграфа. Имеем следующую диаграмму (орграф функции):

Для
нахождения образа
![]() подмножества
подмножества![]() выделим квадратами в множестве
выделим квадратами в множестве![]() вершины из
вершины из![]() а элементы, в которые ведут стрелки из
выделенных вершин кружками.
Имеем:
а элементы, в которые ведут стрелки из
выделенных вершин кружками.
Имеем:

Исходя
из полученной диаграммы, находим ответ:
![]() .
.
Для
нахождения прообраза
![]() подмножества
подмножества![]() в множестве
в множестве![]() выделим квадратами вершины из
выделим квадратами вершины из![]() ,
а элементы, из которых ведут стрелки
в выделенные элементы кружками.
Имеем:
,
а элементы, из которых ведут стрелки
в выделенные элементы кружками.
Имеем:

Исходя
из полученной диаграммы, находим ответ:
![]() .
.
Для
нахождения прообраза
![]() элемента
элемента![]() заметим, что по определению,
заметим, что по определению,![]() .
.
Таким образом, третья часть задачи решается методом аналогичным, использованному методу для второй части задачи.
Применяя
этот метод, находим ответ:
![]() .
.