2Оптимізаційне проектування передавального рядового зубчатого механізму

2.1 Початкові дані

-модуль зубців;

-допустимі напруження кручення ;

-віднесений до модуля крутний момент

-віднесений до модуля максимальний габарит

- віднесений до модуля максимальний габарит

- рекомендовані для дослідження значення коефіцієнту перекриття :

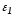=1,57;

=1,58;

=1,59;

=1,6;

- крутний момент ;

- максимальний габарит ;

- максимальний габарит ;

- загальне передаточне відношення зубчатого механізму ;

- інтервали варіювання чисел зубців вхідної шестерні ;

- інтервали варіювання чисел зубців паразитного зубчатого колеса.

Узагальнені математичні моделі для показників, що контролюються при проведенні дослідження:

;

(2.1.1)

;

(2.1.2)

(2.1.3)

2.2 Формалізований опис задачі оптимізаційного проектування

В даному розділі курсового проекту виконується проектування розповсюдженого в техніці рядового зубчатого механізму, кінематична схема якого подана в графічній частині на аркуші 1. Механізм містить вхідну шестерню 1 (з кількістю зубців ), паразитне зубчате колесо 2 (з кількістю зубців) і вихідне зубчате колесо 3 (з кількістю зубців). Для кожного варіанта загальне передаточне відношення механізму дорівнює.

Виконання дослідження передбачає вибір з наданих інтервалів варіювання чисел зубців вхідної шестерні і паразитного колеса.

таких значень, при яких би габарити механізму не перевищували за розрахунковими вимірами ізаданих граничних значеньіі забезпечувалось найбільше значення коефіцієнту перекриття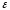для першої ступені механізму (зачеплення коліс 1 і 2).

Відповідно до цього етап проектування механізму розглядається як задача багатомірної оптимізації, при розв’язанні якої коефіцієнт перекриття доцільно вибрати в якості основного критеріального показника, граничні значення габаритів механізмуіураховуються в вигляді функціональних обмежень, а задані інтервали варіювання чисел зубців (керованих змінних)і– у вигляді параметричних обмежень. Тоді математичний запис задачі, що розглядається, буде мати вигляд

,	(2.2.1)

де 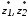– оптимальні значення чисел зубціві;

–максимально можливе значення коефіцієнту перекриття при заданих інтервалах варіювання зміннихіз урахуванням функціональних обмежень за габаритамиі.

При цьому область можливих рішень, що визначається інтервалами варіювання змінних і

.

(2.2.2)

Область припустимих рішень з урахуванням функціональних обмежень

.

(2.2.3)

Остаточно обґрунтований вибір оптимальних значень чисел зубців () виконується за допоміжним графіком, на якому з використанням УММ (1.1.1)…(1.1.3) будуються ізолінії функціональних обмежень, а також чотири ізолінії для рекомендованих початковими даними фіксованих значень коефіцієнта перекриття .

За отриманими значеннями івиконується розробка кінематичної схеми рядового зубчатого механізму, що проектується.

Дана схема повинна викреслюватися на форматі з використанням стандартного масштабу. Нижче подані розрахункові залежності для визначення основних геометричних параметрів механізму.

Діаметри окружностей вершин

(2.2.4)

Діаметри ділильних окружностей

(2.2.5)

Міжцентрові відстані за ступенями

	(2.2.6)
	(2.2.7)

Розрахункові максимальні габарити механізму

	(2.2.8)
	(2.2.9)