- •Задачи для самостоятельного решения
- •В механическом цехе завода фланцы крышек обрабатывают на 7 агрегатных станках. Результаты контроля за качеством крышек приведены в таблице.
- •Контрольную работу выполнили курсанты шести групп первого курса. Результаты контрольной работы приведены в таблице.
- •Фирма, выпускающая прибор, провела маркетинговое исследование, опросив 100 покупателей. Полученные данные о месте покупки изделия и источнике сведений о нем приведены в таблице:
- •9.42. Произведено 500 измерений ошибок наводки при стрельбе по движущим целям. Результаты измерений в делениях угломера представлены статистическим рядом.
- •9.43. С целью исследования закона распределения ошибок измерений дальности дальномером дс-20 произведено 400 измерений дальности. Результаты измерений представлены в таблице
- •9.44. Результаты измерений массы 1000 снарядов калибра 203,2мм представлены в таблице.
- •9.45. В таблице представлены результаты проверки датчика случайных чисел.
- •9.46. Величины отклонений точек падения 250 снарядов от центра рассеивания приведены в таблице.
- •9.82. Во время экзаменов студентам были предложены задачи из семи разделов изучаемого курса. Результаты экзамена приведены в таблице.
- •9.83. В механическом цехе завода фланцы крышек обрабатывают на 7 агрегатных станках. Результаты контроля за качеством крышек приведены в таблице.
- •Задания для самостоятельного решения
9. ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ
9.1. F-распределение и проверка гипотезы о равенстве дисперсий двух нормальных генеральных совокупностей.
9.2.
Проверка гипотезы о равенстве
статистической оценки дисперсии
 и дисперсии
и дисперсии
 генеральной совокупности.
генеральной совокупности.
9.3. Проверка гипотезы о равенстве средних по двум выборкам из нормальных совокупностей.
9.4. Проверка гипотезы о равенстве статистической оценки математического ожидания заданному значению по выборке из нормальной генеральной совокупности.
9.5. Проверка гипотезы об однородности ряда дисперсий по выборкам различного объема. Критерий Бартлетта.
9.6. Проверка гипотезы об однородности ряда дисперсий по выборкам одинакового объема. Критерий Кохрана.
9.7. Проверка гипотез о вероятности в случае биномиального распределения.
9.8. Проверка гипотез об однородности ряда вероятностей в случае полиномиального распределения.
9.9. Проверка гипотезы о виде закона распределения.
9.10. Оценка сомнительных результатов.
Задачи для самостоятельного решения
-
По результатам 8 замеров установлено, что среднее время изготовления детали
 48
с. Предполагая, что время изготовления
есть нормальная случайная величина с
48
с. Предполагая, что время изготовления
есть нормальная случайная величина с
 3
с, необходимо:
3
с, необходимо:
а)
проверить на уровне значимости
 0,01
гипотезу
0,01
гипотезу
 50
c.
против конкурирующей гипотезы
50
c.
против конкурирующей гипотезы
 45
с.;
45
с.;
б) вычислить мощность критерия;
в)
проверить на уровне значимости
 0,01
гипотезу
0,01
гипотезу
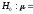 50
c.
против конкурирующей гипотезы
50
c.
против конкурирующей гипотезы
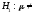 50
c.
50
c.
-
На контрольных испытаниях
 16
ламп было определено
16
ламп было определено
 297
ч. Считая, что срок службы ламп распределен
нормально с
297
ч. Считая, что срок службы ламп распределен
нормально с
 20
ч, необходимо:
20
ч, необходимо:
а)
проверить на уровне значимости
 0,05
гипотезу
0,05
гипотезу
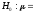 300
ч против конкурирующей гипотезы
300
ч против конкурирующей гипотезы
 290
ч;
290
ч;
б) вычислить мощность критерия;
в)
на уровне значимости
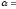 0,08
проверить гипотезу
0,08
проверить гипотезу
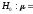 300
ч при конкурирующей гипотезе
300
ч при конкурирующей гипотезе
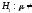 300
ч.
300
ч.
-
В таблице приведены данные об урожайности пшеницы на 8 опытных участках одинакового размера.
|
Участки |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
Урожайность (ц/га) |
26,5 |
25,2 |
28,9 |
30,1 |
32,3 |
29,3 |
26,1 |
25,0 |
Предполагается, что урожайность пшеницы есть нормальная случайная величина. Требуется:
а)
на уровне значимости
 0,1
проверить гипотезу
0,1
проверить гипотезу
 28
ц/га против конкурирующей гипотезы
28
ц/га против конкурирующей гипотезы
 30
ц/га;
30
ц/га;
б) по условию а) вычислить мощность критерия;
в)
проверить на уровне значимости
 0,002
гипотезу
0,002
гипотезу
 29
ц/га против конкурирующей гипотезы
29
ц/га против конкурирующей гипотезы
 29
ц/га.
29
ц/га.
-
При обработке данных 7 испытаний пограничного катера получены следующие значения его максимальной скорости: 38, 49, 42, 46, 45, 41, 39 км/ч. Полагая, что максимальная скорость катера имеет нормальное распределение, проверить на уровне значимости 0,05 гипотезу
 45
км/ч:
45
км/ч:
а)
при конкурирующей гипотезе
 40
км/ч,
40
км/ч,
б)
при конкурирующей гипотезе
 45
км/ч;
45
км/ч;
в) по условию а) задачи вычислить мощность критерия.
-
По данным 12 рейсов установлено, что в среднем машина затрачивает на поездку до склада боеприпасов
 73
мин. Допустив, что время поездки есть
нормальная случайная величина, на
уровнях значимости 0,05 и 0,1 проверить
гипотезу
73
мин. Допустив, что время поездки есть
нормальная случайная величина, на
уровнях значимости 0,05 и 0,1 проверить
гипотезу
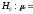 75
мин:
75
мин:
а)
при конкурирующей гипотезе
 72
мин, если известно, что
72
мин, если известно, что
 4
мин;
4
мин;
б)
при конкурирующей гипотезе
 72
мин, если выборочное среднее квадратическое
отклонение равно
72
мин, если выборочное среднее квадратическое
отклонение равно
 4
мин;
4
мин;
в) для условий а) и б) вычислить мощность критерия.
-
При 7 независимых измерениях диаметра поршня одним и тем же прибором получены следующие результаты: 82,45; 82,30; 82,48; 82,05; 82,45; 82,60; 82,46 мм. В предположении, что ошибки измерений имеют нормальное распределение и не содержат систематической ошибки на уровнях значимости 0,05 и 0,2, проверить гипотезу
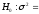 0,02
мм2:
0,02
мм2:
а)
при конкурирующей гипотезе
 0,05
мм2;
0,05
мм2;
б)
при конкурирующей гипотезе
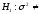 0,02
мм2;
0,02
мм2;
в)
при конкурирующей гипотезе
 >
0,02;
>
0,02;
г) для условия а) вычислить мощность критерия.
-
На основании 12 измерений найдено, что средняя высота сальниковой камеры равна
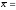 67
мм и
67
мм и
 0,7
мм. Допустив, что ошибка изготовления
есть нормальная случайная величина,
на уровне значимости 0,01 проверить
гипотезу
0,7
мм. Допустив, что ошибка изготовления
есть нормальная случайная величина,
на уровне значимости 0,01 проверить
гипотезу
 0,5
мм2:
0,5
мм2:
а)
при конкурирующей гипотезе
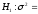 0,1
мм2;
0,1
мм2;
б)
при конкурирующей гипотезе
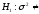 0,5
мм2;
0,5
мм2;
в)
при конкурирующей гипотезе
 >0,5
мм2;
>0,5
мм2;
г) по условию а) задачи вычислить мощность критерия.
-
Точность работы автоматической линии проверяют по дисперсии контролируемого признака, которая не должна превышать
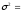 0,11. По результатам выборочного контроля
получены следующие данные:
0,11. По результатам выборочного контроля
получены следующие данные:
|
Контролируемый
размер
|
63,0 |
63,5 |
63,8 |
64,4 |
64,6 |
|
Частота
|
3 |
7 |
10 |
8 |
2 |
Требуется проверить на уровне значимости 0,01, обеспечивает ли линия требуемую точность.
-
Из продукции двух автоматических линий, обрабатывающих корпуса вентилей одного типоразмера, взяты выборки объемом соответственно
 14
и
14
и
 9
корпусов. По результатам выборочных
наблюдений найдено
9
корпусов. По результатам выборочных
наблюдений найдено
 182
мм,
182
мм,
 185
мм. Предварительно установлено, что
погрешности изготовления есть нормальные
случайные величины с дисперсиями
185
мм. Предварительно установлено, что
погрешности изготовления есть нормальные
случайные величины с дисперсиями
 5
мм2
и
5
мм2
и
 7
мм2
. Требуется на уровнях значимости
0,025 и 0,075 проверить гипотезу
7
мм2
. Требуется на уровнях значимости
0,025 и 0,075 проверить гипотезу
 :
:
а)
при конкурирующей гипотезе
 ;
;
б)
при конкурирующей гипотезе
 .
.
-
По двум независимым выборкам объемом
 25
и
25
и
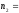 12,
извлеченным неформальных генеральных
совокупностей, найдены выборочные
средние
12,
извлеченным неформальных генеральных
совокупностей, найдены выборочные
средние
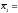 1350
и
1350
и
 1375.
Дисперсии генеральных совокупностей
известны -
1375.
Дисперсии генеральных совокупностей
известны -
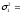 120
и
120
и
 100.
На уровне значимости 0,01 проверить
нулевую гипотезу
100.
На уровне значимости 0,01 проверить
нулевую гипотезу
 при конкурирующей гипотезе
при конкурирующей гипотезе
 .
. -
Расход сырья на единицу продукции по старой технологии составил:
|
Расход
сырья
|
304 |
307 |
312 |
|
Число
изделий
|
2 |
6 |
3 |
Расход сырья по новой технологии составил:
|
Расход
сырья
|
292 |
304 |
308 |
314 |
|
Число
изделий
|
2 |
7 |
4 |
1 |
Предположив,
что расходы сырья в обоих случаях есть
нормальные случайные величины с
одинаковыми средними квадратическими
отклонениями и генеральными средними
 и
и
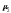 ,
проверить на уровне значимости 0,1
нулевую гипотезу
,
проверить на уровне значимости 0,1
нулевую гипотезу
 против конкурирующей гипотезы: а)
против конкурирующей гипотезы: а)
 ;
б)
;
б)
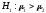 .
.
-
Из продукции двух станков-автоматов, выпускающих однотипные изделия, взяты выборки объемом
 10
и
10
и
 13.
По результатам выборок найдены
13.
По результатам выборок найдены
 82,7
мм,
82,7
мм,
 82,3
мм,
82,3
мм,
 0,8
и
0,8
и
 1,1.
В предположении о нормальном законе
распределения погрешностей изготовления
требуется на уровне значимости
1,1.
В предположении о нормальном законе
распределения погрешностей изготовления
требуется на уровне значимости
 0,01
проверить гипотезу
0,01
проверить гипотезу
 при
конкурирующей гипотезе: а)
при
конкурирующей гипотезе: а)
 ;
б)
;
б)
 .
. -
Для сравнения точности двух станков-автоматов взяты две выборки объемом
 10
и
10
и
 9.
По результатам измерения контролируемого
размера вычислены выборочные дисперсии
9.
По результатам измерения контролируемого
размера вычислены выборочные дисперсии
 0,95,
0,95,
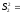 2,75
и
2,75
и
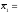 64,3
мм,
64,3
мм,
 64,8
мм. На уровне значимости 0,01 проверить
нулевую гипотезу
64,8
мм. На уровне значимости 0,01 проверить
нулевую гипотезу
 против конкурирующей гипотезы
против конкурирующей гипотезы
 .
. -
По результатам двух независимых выборок объемом
 9
и
9
и
 15,
извлеченных из нормальных генеральных
совокупностей, найдены исправленные
выборочные дисперсии
15,
извлеченных из нормальных генеральных
совокупностей, найдены исправленные
выборочные дисперсии
 24,1
и
24,1
и
 8,6,
а также
8,6,
а также
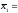 46,9
мм и
46,9
мм и
 47,2
мм. Проверить на уровне значимости 0,05
нулевую гипотезу о равенстве дисперсий
генеральных совокупностей, т.е.
47,2
мм. Проверить на уровне значимости 0,05
нулевую гипотезу о равенстве дисперсий
генеральных совокупностей, т.е.
 при
конкурирующей гипотезе
при
конкурирующей гипотезе
 .
. -
По четырем независимым выборкам объемом
 11,
11,
 15,
15,
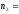 16
и
16
и
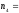 20,
извлеченным из нормальных генеральных
совокупностей, найдены выборочные
дисперсии, равные соответственно
3,5; 2,5; 4,0; 5,5. Проверить на уровне значимости
0,02 гипотезу об однородности дисперсий
20,
извлеченным из нормальных генеральных
совокупностей, найдены выборочные
дисперсии, равные соответственно
3,5; 2,5; 4,0; 5,5. Проверить на уровне значимости
0,02 гипотезу об однородности дисперсий
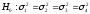 .
. -
Сравнивают точность обработки деталей на четырех станках. Наибольшую точность имеет тот станок, дисперсия контролируемого параметра которого меньше. На первом станке обработано 8 деталей, на втором - 12, на третьем и четвертом по 16 деталей. Исправленные выборочные дисперсии
 соответственно
равны: 0,0051; 0,0038; 0,0064; 0,0028. Допустив, что
ошибки изготовления распределены
нормально, на уровне значимости 0,025
проверить гипотезу о том, что все станки
имеют одинаковую точность.
соответственно
равны: 0,0051; 0,0038; 0,0064; 0,0028. Допустив, что
ошибки изготовления распределены
нормально, на уровне значимости 0,025
проверить гипотезу о том, что все станки
имеют одинаковую точность.
-
Три фасовочных автомата настроены на взвешивание одного и того же веса. С целью проверки точностных характеристик автоматов из их продукции взяты выборки объемом
 14;
14;
 16;
16;
 20.
Контрольные взвешивания на эталонных
весах показали, что величина отклонения
веса продукции от заданной величины
составила (в граммах).
20.
Контрольные взвешивания на эталонных
весах показали, что величина отклонения
веса продукции от заданной величины
составила (в граммах).
|
На первом автомате |
||||
|
Отклонение
|
1 |
2 |
4 |
|
|
Частота
|
6 |
4 |
4 |
|
|
На втором автомате |
||||
|
Отклонение
|
2 |
4 |
5 |
7 |
|
Частота
|
5 |
6 |
4 |
1 |
|
На третьем автомате |
||||
|
Отклонение
|
1 |
2 |
5 |
8 |
|
Частота
|
4 |
6 |
8 |
2 |
Требуется:
а) проверить на уровне значимости 0,1 гипотезу о равенстве точностных характеристик (дисперсий) фасовочных автоматов;
б) найти оценку генеральной дисперсии.
-
Пять станков-автоматов выполняют однотипную технологическую операцию. Из продукции каждого станка для контрольных измерений взято по одной выборке из 11 деталей. По результатам выборочных измерений найдены несмещенные оценки дисперсий
 :
0,0121; 0,0256; 0,0196; 0,0336; 0,0161. Допустив, что
погрешность изготовления есть нормальная
случайная величина, проверить при
уровне значимости 0,05 гипотезу о том,
что точечные характеристики (дисперсии)
станков равны.
:
0,0121; 0,0256; 0,0196; 0,0336; 0,0161. Допустив, что
погрешность изготовления есть нормальная
случайная величина, проверить при
уровне значимости 0,05 гипотезу о том,
что точечные характеристики (дисперсии)
станков равны. -
С целью анализа влияния 4 режимов закалки на прочность деталей каждым режимом закалки обработано по 10 деталей. Исправленные значения выборочных дисперсий, характеризующие вариацию прочности деталей
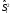 ,
равны: 0,26; 0,36; 0,89; 0,47. Требуется на уровне
значимости 0,01 проверить гипотезу о
равенстве дисперсий, т.е. о независимости
вариации прочности деталей от режима
закалки.
,
равны: 0,26; 0,36; 0,89; 0,47. Требуется на уровне
значимости 0,01 проверить гипотезу о
равенстве дисперсий, т.е. о независимости
вариации прочности деталей от режима
закалки. -
Из продукции 4 станков проконтролировано соответственно
 150,
150,
 50,
50,
 100
и
100
и
 175
изделий, из которых оказались
дефектными
175
изделий, из которых оказались
дефектными
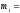 20;
20;
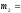 8;
8;
 15
и
15
и
 30
изделий. На уровне значимости 0,01 и 0,05
проверить гипотезу о том, что вероятности
появления дефектного изделия на всех
станках равны, т.е.
30
изделий. На уровне значимости 0,01 и 0,05
проверить гипотезу о том, что вероятности
появления дефектного изделия на всех
станках равны, т.е.
 .
.
-
Во время экзаменов курсантам были предложены задачи из семи разделов изучаемого курса. Результаты экзамена приведены в таблице.
|
Номер раздела курса |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
Число предложенных для решения задач |
165 |
66 |
270 |
160 |
80 |
350 |
150 |
|
Доля решенных задач |
0,855 |
0,509 |
0,522 |
0,484 |
0,860 |
0,412 |
0,420 |
Требуется
на уровне значимости 0,1 проверить
гипотезу о том, что вероятность решения
курсантами задачи не зависит от того,
к какому разделу она относится, т.е.
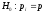 для всех
для всех
 .
.