
- •Часть 1
- •Оглавление
- •Введение
- •1. Механика
- •1.1. Векторы, производные и интегралы
- •1.2. Поступательное движение абсолютно твердого тела (атт)
- •1.2.1. Кинематика частицы и поступательного движения атт
- •1.2.2. Динамика частицы и поступательного движения атт
- •1.3. Вращение атт вокруг неподвижной оси
- •1.3.1. Кинематика вращения атт вокруг неподвижной оси
- •1.3.2. Момент силы. Момент инерции и момент импульса атт
- •1.3.3. Основной закон динамики вращения атт вокруг неподвижной оси
- •1.4. Механическая работа. Энергия. Законы сохранения в механике
- •1.4.1. Механическая работа. Энергия. Закон сохранения энергии
- •1.4.2. Закон сохранения импульса. Столкновение частиц.
- •1.4.3. Закон сохранения момента импульса
- •1.5. Элементы специальной теории относительности
- •2. Молекулярная физика и термодинамика
- •2.1. Уравнение состояния идеального газа. Закон Дальтона
- •2.2. Распределения Максвелла и Больцмана
- •2.3. Первый закон термодинамики. Адиабатный процесс
- •2.4. Теплоемкость. Энтропия. Цикл Карно
- •Библиографический список
- •Приложение
- •Часть 1.
1.3. Вращение атт вокруг неподвижной оси
1.3.1. Кинематика вращения атт вокруг неподвижной оси
Основными
кинематическими характеристиками
вращательного движения твердого тела
являются угловое перемещение (угол
поворота) ,
угловая
скорость
![]() и угловое ускорение
и угловое ускорение![]()
Угол поворота является скалярной величиной, в СИ измеряется в радианах.
Угол поворота связан с числом оборотов N соотношением:
![]() (20)
(20)
Угловая скорость характеризует быстроту вращательного движения и при вращении АТТ вокруг неподвижной оси определяется через производную от угла поворота тела по времени:
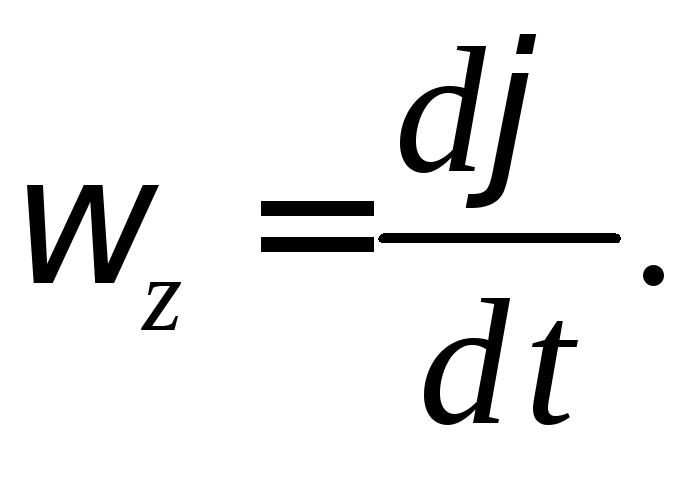 (21)
(21)
Вектор
угловой скорости
![]() направлен вдоль оси вращения тела в ту
сторону, откуда видно вращение,
происходящее против хода часовой
стрелки.
направлен вдоль оси вращения тела в ту
сторону, откуда видно вращение,
происходящее против хода часовой
стрелки.
По известному закону изменения со временем угловой скорости z(t) можно найти закон изменения угла поворота:
 (22)
(22)
Изменение
угловой скорости со временем характеризуется
угловым ускорением. По аналогии с угловой
скоростью угловое ускорение тела также
можно представить в виде вектора
![]() направленного вдоль оси вращения тела.
Направление вектора
направленного вдоль оси вращения тела.
Направление вектора![]() совпадает с направлением вектора
совпадает с направлением вектора![]() ,
когда вращение ускоренное, и противоположно
направлению вектора
,
когда вращение ускоренное, и противоположно
направлению вектора![]() при торможении. Угловое ускорение в
данный момент времени определяется
через первую производнуюот
угловой скорости или вторую производную
от угла поворота тела по времени:
при торможении. Угловое ускорение в
данный момент времени определяется
через первую производнуюот
угловой скорости или вторую производную
от угла поворота тела по времени:
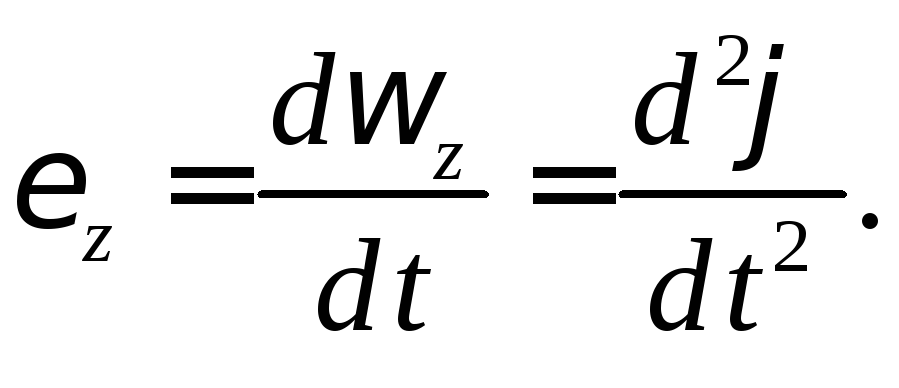 (23)
(23)
Аналогично определению закона изменения угла поворота, можно найти закон изменения со временем угловой скорости:

![]() (24)
(24)
В
случае вращения тела с
![]() из формул (22) и (24) получаются соотношения:
из формул (22) и (24) получаются соотношения:
![]() ;
(25)
;
(25)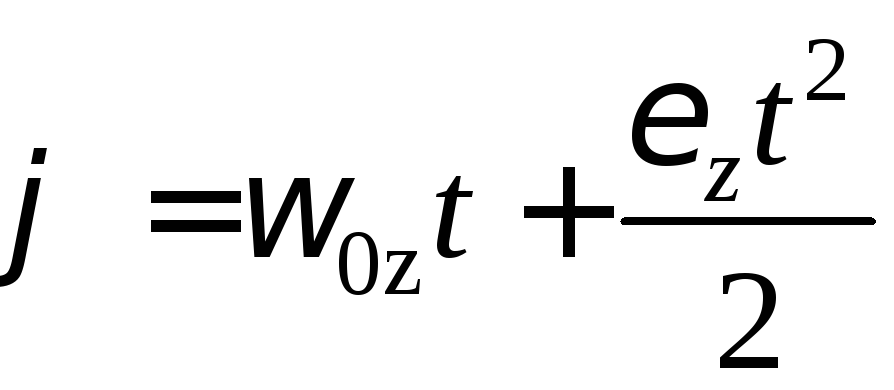 ;
(26)
;
(26)
 ;
(27)
;
(27)
![]() .
(28)
.
(28)
Модули линейной скорости, нормального и тангенциального ускорений связаны с кинематическими характеристиками вращательного движения соотношениями:
![]() ;
(29)
;
(29)
![]() ;
(30)
;
(30)
![]() .
(31)
.
(31)
Задачи
31.(1) Тело, вращаясь равнопеременно, за время 2,3 с изменило угловую скорость от 2,1 рад/с до 0,98 рад/с. Найти угловое ускорение тела.
32.(1) Твердое тело вращается равнопеременно вокруг неподвижной оси. Скорость точки, находящейся на расстоянии 10 см от оси, в начальный момент времени равна 0,95 м/с, а через 5,8 с – 4,0 м/с. Определить через 4,3 с после начала движения: 1) угловую скорость и угловое ускорение тела;2) линейную скорость, тангенциальное, нормальное и полное ускорения указанной точки.
33.(1) Тело, вращаясь равнопеременно, за 5,0 с от начала движения совершило 100 оборотов. Найти угловое ускорение тела.
34.(1) Маховик, вращающийся с частотой 1,8 с1, останавливается через 1,5 мин. Считая движение равнопеременным, найти, сколько оборотов сделал маховик до остановки, и его угловое ускорение.
35.(1) Тело вращается вокруг неподвижной оси. Зависимость угловой скорости от времени приведена на рис. 1. Чему равно угловое ускорение тела?
36.(2) Колесо машины за 120 с изменило частоту вращения от 240 об/мин до 60 об/мин. Найти угловое ускорение колеса и число оборотов, сделанных колесом за это время.
 37.(2)
Колесо
радиусом 110 мм вращается вокруг
оси Оz,
перпендикулярной плоскости колеса и
проходящей через его центр масс так,
что зависимость угла поворота радиуса
колеса от времени задается уравнением:
37.(2)
Колесо
радиусом 110 мм вращается вокруг
оси Оz,
перпендикулярной плоскости колеса и
проходящей через его центр масс так,
что зависимость угла поворота радиуса
колеса от времени задается уравнением:
![]() гдеВ = 2,5 рад/с;
С = 1,8 рад/с3.
Найти через 1,8 с после начала движения
угловую скорость и угловое ускорение
колеса. Для точек, лежащих на ободе
колеса, найти в указанный момент времени:
1) линейную
скорость, 2) тангенциальное,
нормальное и полное ускорения.
гдеВ = 2,5 рад/с;
С = 1,8 рад/с3.
Найти через 1,8 с после начала движения
угловую скорость и угловое ускорение
колеса. Для точек, лежащих на ободе
колеса, найти в указанный момент времени:
1) линейную
скорость, 2) тангенциальное,
нормальное и полное ускорения.
38.(2)
Найти нормальное и тангенциальное
ускорения точки лопатки турбины,
расположенной на расстоянии 1,3 м
от оси вращения, через 15 с
после пуска турбины, если зависимость
модуля линейной скорости лопатки от
времени выражена уравнением:
![]() ,
гдеА = 2,2 м/с2,
В = 0,83 м/с3.
,
гдеА = 2,2 м/с2,
В = 0,83 м/с3.
39.(2)
Диск радиусом 2,2 м
вращается вокруг оси Оz,
перпендикулярной плоскости диска и
проходящей через его центр масс, так,
что угловая скорость диска меняется со
временем по закону:
![]() гдеА = 2,4 рад/с;
В = 3,9 рад/с3.
Вычислить тангенциальное ускорение
точек диска, находящихся от его центра
на расстоянии, равном половине радиуса
диска, в момент времени 3,1 с.
Определить угол, на который повернется
диск за это время.
гдеА = 2,4 рад/с;
В = 3,9 рад/с3.
Вычислить тангенциальное ускорение
точек диска, находящихся от его центра
на расстоянии, равном половине радиуса
диска, в момент времени 3,1 с.
Определить угол, на который повернется
диск за это время.
40.(2)
Зависимость
угловой скорости диска, вращающегося
вокруг оси Оz,
перпендикулярной его плоскости и
проходящей через центр масс диска, от
времени задается законом:
![]() Вычислить
полное ускорение точек, лежащих на краю
диска, в момент времени 0,98 с.
Определить зависимость угла поворота
диска от времени. Радиус диска равен
40 см;
А = 2,5 рад/с3;
В = 2,1 рад/с4.
Вычислить
полное ускорение точек, лежащих на краю
диска, в момент времени 0,98 с.
Определить зависимость угла поворота
диска от времени. Радиус диска равен
40 см;
А = 2,5 рад/с3;
В = 2,1 рад/с4.
