
Кр_ТВ_Э
.pdf0; |
|
х < 1, |
|
|
2 |
; − 1 ≤ х ≤ 1, |
α=-0,5; β=2. |
59. f (x) = A(x + 1) |
|
||
|
|
х > 1. |
|
0; |
|
|
|
0; |
|
х ≤ 0, |
|
|
|
0 ≤ х ≤ 3, |
α=1; β=2. |
60. f (x) = Ax; |
|
||
|
|
х > 3. |
|
0; |
|
|
61 – 70: Нормально распределенная случайная величина X задана своими параметрами а (математическое ожидание) и σ(среднее квадратическое отклонение). Требуется:
а) записать выражение для функции распределения, схематически изобразить ее график;
б) определить вероятность того, что X примет значение из интервала (α; β);
в) определить вероятность того, что X отклонится (по модулю) от а не более чем на δ.
61. |
a = 3; |
σ = 4; |
62. |
a = 3; |
σ = 3; |
63. |
а = 4; |
σ = 5; |
64. |
а = 4; |
σ = 4; |
65. |
a = -2; |
σ = 3; |
66. |
a = -5; |
σ = 4; |
67. |
a = 10; |
σ = 2; |
68. |
a = 5; |
σ = 1; |
69. |
a = 4; |
σ = 2; |
70. |
a = 6; |
σ = 6; |
α = 2; |
β = 8; |
δ = 3. |
α = 0; |
β = 7; |
δ = 3. |
α = 1; |
β = 9; |
δ = 2. |
α = -1; |
β = 7; |
δ = 3 |
α = -5; |
β = 4; |
δ = 3. |
α = -8; |
β = 0; |
δ = 2. |
α = 6; |
β = 12; |
δ = 3. |
α = 3; |
β = 8; |
δ = 3. |
α = 0; |
β = 9; |
δ = 4. |
α = 5; |
β = 7; |
δ = 4. |
ЗАДАНИЯ ДЛЯ КОНТРОЛЬНОЙ РАБОТЫ № 2
Дана двумерная выборка дискретных случайных величин Х= {x1, х2,..., хn} и Y= { y1, y2,..., yn }.
Требуется:
1.Построить вариационные ряды для величин хi и yi.
2.Используя вариационные ряды, составить интервальные ряды распределения величин Х и Y. Длины интервалов hx и hy найти по формуле Стерджеса.
3.Построить гистограммы относительных интервальных частот величин X и Y. На основе гистограмм построить графики эмпирических функций плотностей вероятностей величин Х и Y.
4.Найти моду и медиану для интервальных распределений X и Y.
5.Используя данные вариационных рядов, найти статистические средние значения, дисперсии и средние квадратические отклонения Х и Y. Используя середины интервалов
ичастоты интервалов, найти выборочные средние, выборочные дисперсии и выборочные средние квадратические отклонения Х и Y. Сделать сравнение вычисленных величин.
41

6.Найти доверительные интервалы для оценок математического ожидания и дисперсии величин X и Y в предположении о нормальном распределении с доверительной вероятностью β = 0,9.
7.Считая средние интервальные значения Х и Y распределенным и по нормальному закону, вычислить для каждого интервала теоретические относительные частоты для X и Y. По найденным частотам построить на одном рисунке с гистограммой графики теоретических функций плотностей вероятностей случайных величин Х и Y.
8.В случае качественного совпадения графиков эмпирических и теоретических функций плотностей вероятностей проверить гипотезу о нормальном распределении случайных величин X и Y с помощью критерия Пирсона при уровне значимости а = 0,05.
9.Используя интервальные ряды распределения, составить корреляционную таблицу.
10.Найти выборочный коэффициент корреляции в предположении линейной зависимости между X и Y.
11.Найти выборочные уравнения прямой линии регрессии Y на Х и прямой линии регрессии Х на Y. Построить их на корреляционном поле.
Вариант 1.
X |
Y |
X |
Y |
X |
Y |
X |
Y |
X |
Y |
72 |
55 |
106 |
79 |
86 |
67 |
89 |
74 |
102 |
76 |
92 |
74 |
90 |
70 |
104 |
77 |
104 |
78 |
112 |
86 |
107 |
79 |
92 |
74 |
74 |
58 |
95 |
79 |
96 |
74 |
81 |
70 |
111 |
83 |
76 |
58 |
114 |
84 |
82 |
62 |
11О |
82 |
94 |
70 |
91 |
68 |
91 |
68 |
81 |
61 |
100 |
77 |
103 |
78 |
91 |
70 |
87 |
66 |
83 |
64 |
95 |
78 |
98 |
75 |
95 |
73 |
87 |
68 |
107 |
79 |
82 |
62 |
93 |
71 |
97 |
74 |
81 |
66 |
98 |
74 |
86 |
70 |
87 |
66 |
98 |
75 |
99 |
75 |
83 |
62 |
96 |
76 |
109 |
83 |
99 |
76 |
113 |
83 |
84 |
67 |
104 |
81 |
91 |
71 |
109 |
81 |
113 |
86 |
89 |
69 |
98 |
75 |
100 |
76 |
105 |
78 |
84 |
65 |
69 |
55 |
97 |
73 |
101 |
80 |
100 |
74 |
101 |
75 |
95 |
71 |
91 |
75 |
88 |
67 |
103 |
79 |
92 |
70 |
103 |
78 |
88 |
66 |
83 |
66 |
95 |
74 |
85 |
67 |
96 |
76 |
103 |
77 |
82 |
62 |
106 |
79 |
82 |
65 |
107 |
82 |
92 |
69 |
90 |
70 |
84 |
71 |
82 |
64 |
97 |
79 |
90 |
67 |
99 |
78 |
83 |
63 |
106 |
81 |
77 |
58 |
101 |
77 |
108 |
81 |
83 |
70 |
113 |
85 |
101 |
75 |
84 |
63 |
87 |
67 |
85 |
67 |
89 |
69 |
90 |
69 |
42

Вариант 2
X |
Y |
X |
Y |
X |
Y |
X |
Y |
X |
Y |
37 |
79 |
30 |
71 |
36 |
78 |
34 |
11 |
39 |
84 |
43 |
88 |
29 |
69 |
39 |
86 |
40 |
85 |
37 |
83 |
38 |
83 |
38 |
82 |
31 |
71 |
38 |
83 |
44 |
95 |
35 |
75 |
37 |
79 |
48 |
97 |
37 |
81 |
33 |
75 |
41 |
87 |
36 |
80 |
36 |
78 |
30 |
71 |
37 |
84 |
43 |
88 |
31 |
77 |
43 |
90 |
34 |
75 |
38 |
82 |
26 |
62 |
42 |
88 |
37 |
79 |
42 |
88 |
36 |
79 |
37 |
80 |
32 |
76 |
46 |
98 |
42 |
93 |
43 |
90 |
42 |
86 |
39 |
81 |
46 |
93 |
35 |
84 |
41 |
86 |
30 |
68 |
36 |
80 |
41 |
84 |
43 |
90 |
26 |
65 |
35 |
78 |
33 |
74 |
38 |
82 |
36 |
83 |
38 |
80 |
34 |
81 |
33 |
74 |
45 |
90 |
31 |
69 |
48 |
95 |
44 |
89 |
37 |
81 |
40 |
83 |
39 |
86 |
34 |
74 |
31 |
72 |
34 |
77 |
35 |
77 |
36 |
77 |
45 |
90 |
36 |
79 |
48 |
97 |
25 |
63 |
39 |
84 |
35 |
78 |
37 |
85 |
34 |
76 |
36 |
77 |
46 |
93 |
31 |
71 |
34 |
75 |
38 |
80 |
39 |
83 |
35 |
76 |
34 |
75 |
42 |
86 |
37 |
80 |
40 |
83 |
36 |
80 |
50 |
99 |
40 |
83 |
33 |
73 |
33 |
77 |
50 |
98 |
32 |
74 |
33 |
75 |
39 |
82 |
26 |
64 |
39 |
84 |
42 |
86 |
Вариант 3
X |
Y |
X |
Y |
X |
|
Y |
X |
Y |
X |
Y |
89 |
69 |
76 |
78 |
81 |
|
69 |
81 |
74 |
62 |
89 |
95 |
61 |
92 |
61 |
94 |
|
57 |
86 |
69 |
73 |
76 |
79 |
76 |
78 |
72 |
83 |
|
80 |
73 |
79 |
65 |
88 |
96 |
58 |
66 |
88 |
83 |
|
73 |
73 |
81 |
80 |
71 |
79 |
76 |
85 |
65 |
88 |
|
63 |
89 |
62 |
71 |
80 |
93 |
59 |
78 |
84 |
67 |
|
87 |
91 |
65 |
81 |
74 |
72 |
82 |
76 |
74 |
77 |
|
83 |
68 |
80 |
80 |
73 |
95 |
61 |
66 |
83 |
69 |
|
79 |
83 |
67 |
93 |
62 |
86 |
64 |
83 |
72 |
80 |
|
73 |
70 |
84 |
89 |
66 |
99 |
59 |
91 |
72 |
78 |
|
77 |
91 |
63 |
77 |
77 |
91 |
73 |
90 |
66 |
67 |
|
84 |
77 |
78 |
100 |
57 |
92 |
60 |
88 |
67 |
102 |
|
55 |
85 |
65 |
83 |
80 |
88 |
68 |
87 |
65 |
71 |
|
83 |
73 |
81 |
76 |
78 |
77 |
74 |
81 |
70 |
71 |
|
83 |
80 |
69 |
79 |
84 |
80 |
73 |
81 |
72 |
77 |
|
72 |
85 |
77 |
78 |
80 |
77 |
77 |
71 |
88 |
74 |
|
75 |
71 |
79 |
81 |
77 |
83 |
79 |
82 |
68 |
85 |
|
70 |
71 |
82 |
76 |
80 |
60 |
91 |
87 |
63 |
92 |
|
64 |
81 |
71 |
91 |
65 |
92 |
64 |
79 |
82 |
73 |
|
79 |
71 |
82 |
78 |
83 |
82 |
69 |
85 |
70 |
76 |
|
82 |
79 |
75 |
86 |
65 |
|
|
|
|
|
43 |
|
|
|
|
|

Вариант 4
X |
Y |
X |
Y |
X |
Y |
X |
Y |
X |
Y |
84 |
75 |
99 |
-88 |
106 |
93 |
104 |
90 |
113 |
98 |
108 |
95 |
105 |
90 |
89 |
78 |
112 |
97 |
96 |
87 |
90 |
81 |
97 |
86 |
87 |
77 |
90 |
82 |
80 |
72 |
101 |
89 |
92 |
81 |
92 |
83 |
92 |
81 |
98 |
85 |
94 |
82 |
98 |
85 |
99 |
93 |
104 |
92 |
96 |
83 |
97 |
91 |
110 |
93 |
101 |
88 |
92 |
80 |
87 |
83 |
96 |
84 |
109 |
93 |
89 |
80 |
94 |
85 |
108 |
94 |
89 |
85 |
106 |
93 |
86 |
79 |
110 |
101 |
92 |
81 |
102 |
90 |
93 |
87 |
94 |
82 |
97 |
84 |
78 |
73 |
84 |
75 |
89 |
80 |
85 |
78 |
109 |
95 |
98 |
86 |
91 |
81 |
102 |
93 |
115 |
98 |
106 |
90 |
111 |
97 |
82 |
73 |
109 |
97 |
119 |
102 |
96 |
85 |
98 |
88 |
85 |
76 |
98 |
85 |
105 |
93 |
89 |
81 |
79 |
76 |
82 |
76 |
100 |
89 |
99 |
92 |
102 |
88 |
98 |
90 |
112 |
98 |
96 |
87 |
94 |
83 |
100 |
90 |
87 |
77 |
93 |
82 |
105 |
91 |
99 |
85 |
87 |
77 |
76 |
71 |
92 |
82 |
80 |
72 |
114 |
97 |
107 |
95 |
104 |
90 |
105 |
92 |
110 |
94 |
89 |
80 |
91 |
80 |
92 |
83 |
105 |
90 |
96 |
87 |
72 |
66 |
97 |
85 |
94 |
84 |
104 |
90 |
107 |
97 |
90 |
79 |
81 |
73 |
85 |
16 |
Вариант 5
X |
Y |
X |
Y |
X |
|
Y |
X |
Y |
X |
Y |
44 |
32 |
41 |
-34 |
52 |
|
37 |
44 |
32 |
37 |
27 |
45 |
31 |
41 |
28 |
44 |
|
32 |
47 |
36 |
50 |
36 |
42 |
30 |
36 |
24 |
38 |
|
25 |
52 |
37 |
40 |
29 |
44 |
31 |
52 |
39 |
39 |
|
27 |
40 |
26 |
39 |
31 |
41 |
29 |
54 |
40 |
36 |
|
23 |
40 |
27 |
40 |
27 |
42 |
32 |
40 |
27 |
51 |
|
40 |
54 |
41 |
44 |
32 |
38 |
28 |
41 |
27 |
40 |
|
31 |
45 |
31 |
44 |
32 |
47 |
33 |
40 |
26 |
39 |
|
27 |
43 |
29 |
52 |
38 |
45 |
31 |
55 |
44 |
49 |
|
37 |
36 |
28 |
37 |
25 |
32 |
21 |
42 |
30 |
41 |
|
30 |
39 |
29 |
42 |
28 |
43 |
30 |
42 |
28 |
48 |
|
36 |
44 |
30 |
44 |
33 |
44 |
33 |
37 |
24 |
43 |
|
29 |
37 |
26 |
39 |
26 |
36 |
23 |
41 |
28 |
42 |
|
32 |
38 |
26 |
49 |
36 |
44 |
31 |
46 |
32 |
40 |
|
28 |
39 |
25 |
43 |
30 |
44 |
31 |
46 |
2 |
39 |
|
29 |
51 |
38 |
44 |
31 |
45 |
35 |
44 |
32 |
37 |
|
25 |
36 |
26 |
46 |
32 |
35 |
23 |
43 |
31 |
38 |
|
25 |
47 |
33 |
34 |
22 |
34 |
22 |
31 |
19 |
46 |
|
33 |
46 |
32 |
37 |
24 |
47 |
33 |
36 |
24 |
49 |
|
38 |
50 |
35 |
46 |
32 |
45 |
32 |
47 |
34 |
32 |
|
19 |
48 |
38 |
41 |
29 |
|
|
|
|
|
44 |
|
|
|
|
|

Вариант 6
X |
Y |
X |
Y |
X |
Y |
X |
Y |
X |
Y |
64 |
91 |
68 |
100 |
64 |
94 |
65 |
96 |
64 |
90 |
60 |
88 |
61 |
87 |
68 |
96 |
55 |
84 |
55 |
78 |
65 |
92 |
68 |
96 |
63 |
92 |
62 |
88 |
63 |
92 |
58 |
83 |
68 |
106 |
64 |
89 |
74 |
106 |
67 |
94 |
46 |
66 |
64 |
94 |
54 |
75 |
56 |
79 |
61 |
88 |
67 |
98 |
50 |
72 |
65 |
91 |
55 |
77 |
52 |
75 |
68 |
103 |
59 |
82 |
63 |
93 |
76 |
108 |
52 |
72 |
64 |
94 |
48 |
66 |
60 |
91 |
65 |
101 |
57 |
84 |
68 |
99 |
66 |
92 |
77 |
108 |
57 |
83 |
62 |
86 |
66 |
95 |
67 |
97 |
66 |
94 |
48 |
71 |
55 |
81 |
69 |
101 |
65 |
91 |
64 |
94 |
55 |
81 |
76 |
115 |
61 |
90 |
65 |
95 |
63 |
93 |
57 |
83 |
66 |
92 |
70 |
104 |
65 |
91 |
62 |
95 |
70 |
100 |
74 |
105 |
54 |
86 |
62 |
87 |
73 |
107 |
70 |
99 |
63 |
100 |
77 |
120 |
63 |
93 |
69 |
100 |
71 |
99 |
63 |
93 |
66 |
97 |
61 |
97 |
53 |
74 |
54 |
83 |
69 |
109 |
57 |
80 |
72 |
101 |
60 |
85 |
81 |
116 |
77 |
120 |
68 |
98 |
69 |
109 |
71 |
104 |
63 |
92 |
59 |
87 |
71 |
99 |
73 |
106 |
48 |
71 |
60 |
85 |
70 |
105 |
59 |
87 |
63 |
89 |
71 |
104 |
54 |
86 |
55 |
78 |
Вариант 7
X |
Y |
X |
Y |
X |
|
Y |
X |
Y |
X |
Y |
73 |
89 |
68 |
89 |
78 |
|
96 |
78 |
92 |
79 |
94 |
62 |
82 |
87 |
100 |
75 |
|
90 |
61 |
82 |
72 |
89 |
67 |
86 |
67 |
87 |
55 |
|
78 |
65 |
87 |
71 |
90 |
60 |
81 |
59 |
82 |
76 |
|
93 |
76 |
92 |
62 |
83 |
76 |
91 |
83 |
96 |
58 |
|
81 |
68 |
87 |
72 |
89 |
82 |
95 |
64 |
85 |
61 |
|
82 |
71 |
88 |
52 |
76 |
70 |
88 |
82 |
97 |
75 |
|
92 |
82 |
95 |
79 |
97 |
77 |
94 |
79 |
95 |
74 |
|
95 |
63 |
87 |
70 |
88 |
59 |
81 |
67 |
87 |
75 |
|
90 |
64 |
85 |
86 |
97 |
65 |
84 |
66 |
85 |
70 |
|
87 |
67 |
85 |
70 |
87 |
79 |
95 |
67 |
86 |
80 |
|
95 |
67 |
86 |
93 |
105 |
75 |
90 |
90 |
105 |
74 |
|
93 |
67 |
90 |
78 |
95 |
75 |
91 |
75 |
92 |
68 |
|
88 |
59 |
80 |
64 |
83 |
71 |
90 |
56 |
78 |
65 |
|
85 |
66 |
88 |
83 |
97 |
58 |
84 |
67 |
86 |
65 |
|
86 |
69 |
87 |
78 |
94 |
64 |
83 |
74 |
90 |
80 |
|
94 |
76 |
93 |
65 |
85 |
69 |
88 |
71 |
88 |
66 |
|
87 |
74 |
91 |
83 |
96 |
65 |
84 |
67 |
86 |
62 |
|
84 |
78 |
94 |
60 |
83 |
76 |
91 |
75 |
90 |
68 |
|
89 |
71 |
89 |
77 |
94 |
67 |
86 |
82 |
97 |
68 |
|
88 |
65 |
86 |
66 |
86 |
|
|
|
|
|
45 |
|
|
|
|
|

Вариант 8
X |
Y |
X |
Y |
X |
Y |
X |
Y |
X |
Y |
51 |
74 |
54 |
78 |
53 |
80 |
57 |
91 |
64 |
91 |
60 |
88 |
51 |
85 |
45 |
70 |
60 |
85 |
77 |
114 |
43 |
64 |
59 |
84 |
61 |
95 |
53 |
76 |
62 |
88 |
49 |
75 |
57 |
82 |
58 |
87 |
56 |
83 |
54 |
81 |
68 |
98 |
52 |
76 |
61 |
87 |
48 |
70 |
58 |
91 |
59 |
87 |
68 |
98 |
65 |
94 |
63 |
90 |
51 |
77 |
47 |
72 |
60 |
86 |
68 |
95 |
51 |
75 |
64 |
93 |
49 |
77 |
67 |
100 |
34 |
63 |
65 |
100 |
65 |
94 |
44 |
68 |
56 |
84 |
58 |
84 |
62 |
90 |
48 |
71 |
54 |
78 |
62 |
91 |
70 |
100 |
53 |
80 |
45 |
67 |
61 |
87 |
57 |
85 |
55 |
81 |
36 |
58 |
52 |
75 |
39 |
61 |
58 |
9, |
48 |
74 |
61 |
87 |
62 |
91 |
53 |
80 |
49 |
77 |
63 |
92 |
63 |
92 |
53 |
80 |
60 |
86 |
59 |
84 |
48 |
72 |
60 |
85 |
40 |
62 |
51 |
77 |
56 |
82 |
49 |
73 |
47 |
73 |
54 |
78 |
44 |
68 |
56 |
87 |
63 |
90 |
63 |
89 |
49 |
75 |
47 |
69 |
60 |
95 |
60 |
87 |
54 |
85 |
72 |
101 |
54 |
84 |
39 |
60 |
42 |
66 |
57 |
82 |
53 |
76 |
59 |
86 |
48 |
72 |
58 |
92 |
43 |
64 |
41 |
65 |
52 |
82 |
67 |
93 |
55 |
80 |
49 |
72 |
49 |
71 |
Вариант 9
X |
Y |
X |
Y |
X |
|
Y |
X |
Y |
X |
Y |
94 |
51 |
86 |
48 |
11 |
|
44 |
90 |
49 |
88 |
48 |
76 |
44 |
70 |
40 |
85 |
|
48 |
78 |
44 |
62 |
38 |
87 |
48 |
85 |
47 |
76 |
|
45 |
84 |
49 |
98 |
52 |
84 |
45 |
67 |
40 |
99 |
|
52 |
78 |
44 |
77 |
45 |
70 |
40 |
99 |
52 |
90 |
|
51 |
83 |
45 |
78 |
44 |
80 |
46 |
93 |
49 |
99 |
|
52 |
72 |
40 |
94 |
51 |
69 |
43 |
85 |
47 |
83 |
|
46 |
80 |
46 |
80 |
45 |
64 |
39 |
90 |
48 |
87 |
|
48 |
104 |
53 |
64 |
37 |
83 |
45 |
61 |
36 |
84 |
|
47 |
65 |
37 |
71 |
42 |
89 |
49 |
76 |
43 |
71 |
|
41 |
90 |
52 |
89 |
48 |
65 |
38 |
63 |
40 |
84 |
|
47 |
75 |
43 |
77 |
42 |
69 |
39 |
93 |
50 |
95 |
|
53 |
82 |
45 |
76 |
44 |
81 |
44 |
73 |
41 |
67 |
|
43 |
59 |
36 |
81 |
47 |
66 |
42 |
101 |
52 |
92 |
|
49 |
96 |
51 |
60 |
37 |
73 |
42 |
85 |
46 |
93 |
|
50 |
51 |
32 |
69 |
42 |
97 |
54 |
66 |
42 |
96 |
|
54 |
75 |
43 |
76 |
43 |
93 |
49 |
82 |
47 |
78 |
|
43 |
78 |
43 |
82 |
45 |
69 |
42 |
83 |
48 |
75 |
|
42 |
70 |
41 |
83 |
46 |
83 |
46 |
65 |
39 |
65 |
|
37 |
74 |
43 |
80 |
45 |
85 |
46 |
75 |
43 |
105 |
|
56 |
66 |
38 |
80 |
47 |
|
|
|
|
|
46 |
|
|
|
|
|

Вариант 10
X |
Y |
X |
Y |
X |
Y |
X |
Y |
X |
Y |
57 |
100 |
63 |
103 |
69 |
106 |
55 |
93 |
39 |
81 |
53 |
91 |
63 |
102 |
55 |
94 |
57 |
99 |
56 |
97 |
55 |
95 |
61 |
99 |
62 |
102 |
54 |
94 |
54 |
94 |
52 |
91 |
57 |
95 |
62 |
100 |
45 |
84 |
62 |
102 |
42 |
81 |
57 |
102 |
58 |
102 |
57 |
103 |
64 |
101 |
71 |
108 |
61 |
103 |
80 |
117 |
65 |
102 |
82 |
120 |
53 |
91 |
59 |
100 |
69 |
110 |
52 |
93 |
47 |
88 |
42 |
84 |
60 |
99 |
58 |
100 |
63 |
102 |
70 |
109 |
51 |
90 |
49 |
90 |
51 |
91 |
54 |
95 |
58 |
102 |
67 |
104 |
66 |
110 |
61 |
100 |
52 |
95 |
61 |
105 |
51 |
92 |
43 |
83 |
43 |
86 |
56 |
102 |
51 |
90 |
53 |
94 |
64 |
101 |
59 |
99 |
60 |
99 |
61 |
104 |
65 |
105 |
63 |
107 |
69 |
109 |
63 |
100 |
62 |
102 |
71 |
109 |
52 |
90 |
60 |
100 |
73 |
111 |
48 |
88 |
71 |
110 |
47 |
93 |
54 |
94 |
67 |
107 |
59 |
98 |
58 |
96 |
60 |
99 |
51 |
90 |
59 |
97 |
46 |
85 |
51 |
96 |
41 |
81 |
69 |
108 |
71 |
111 |
58 |
99 |
68 |
105 |
55 |
95 |
61 |
99 |
71 |
110 |
84 |
125 |
63 |
103 |
64 |
104 |
70 |
115 |
56 |
96 |
45 |
84 |
50 |
93 |
66 |
108 |
63 |
103 |
70 |
106 |
61 |
106 |
47
Библиографический список
1.Гмурман В.Е. Теория вероятностей и математическая статистика. – М.: Высшее образование, 2007. – 479 с.
2.Вентцель Е.С. Теория вероятностей и ее инженерные приложения. – М.: Высшая школа, 2007. – 479 с.
3.Ивченко Г.И. Задачи с решениями по математической статистике. – М.: Дрофа, 2007. – 318 с.
4.Вентцель Е.С., Овчаров Л.А. Задачи и упражнения по теории вероятностей. – М.:
Академия, 2005. – 448 с.
5.Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. – М.: Высшая школа, 2003. – 405 с.
6.Лаврусь О.Е. Конспект лекций по теории вероятностей. – Самара: СамГАПС, 2007. – 88 с.
48
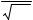
ПРИЛОЖЕНИЕ
|
|
1. Таблица значений функции ϕ (х) = |
1 |
|
e− |
x2 |
|
||||||||
|
|
|
2 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
2π |
|
|
|
|
|
|
|
0 |
|
1 |
2 |
3 |
4 |
5 |
6 |
|
7 |
|
8 |
9 |
||
0,0 |
0,3989 |
|
3989 |
3989 |
3988 |
3986 |
3984 |
3982 |
3980 |
|
3977 |
3973 |
|||
0,1 |
3970 |
|
3965 |
3961 |
3956 |
3951 |
3945 |
3939 |
3932 |
|
3925 |
3918 |
|||
0,2 |
3910 |
|
3902 |
3894 |
3885 |
3876 |
3867 |
3857 |
3847 |
|
3836 |
3825 |
|||
0,3 |
3814 |
|
3802 |
3790 |
3778 |
3765 |
3752 |
3739 |
3726 |
|
3712 |
3697 |
|||
0,4 |
3683 |
|
3668 |
3653 |
3637 |
3621 |
3605 |
3589 |
3572 |
|
3555 |
3538 |
|||
0,5 |
3521 |
|
3503 |
3485 |
3467 |
3448 |
3429 |
3410 |
3391 |
|
3372 |
3352 |
|||
0,6 |
3332 |
|
3312 |
3292 |
3271 |
3251 |
3230 |
3209 |
3187 |
|
3166 |
3144 |
|||
0,7 |
3123 |
|
3101 |
3079 |
3056 |
3034 |
3011 |
2989 |
2966 |
|
2943 |
2920 |
|||
0,8 |
2897 |
|
2874 |
2850 |
2827 |
2803 |
2780 |
2756 |
2732 |
|
2709 |
2685 |
|||
0,9 |
2661 |
|
2637 |
2613 |
2589 |
2565 |
2541 |
2516 |
2492 |
|
2468 |
2444 |
|||
1,0 |
0,2420 |
|
2396 |
2371 |
2347 |
2323 |
2299 |
2275 |
2251 |
|
2227 |
2203 |
|||
1,1 |
2179 |
|
2155 |
2131 |
2107 |
2083 |
2059 |
2036 |
2012 |
|
1989 |
1965 |
|||
1,2 |
1942 |
|
1919 |
1895 |
1872 |
1849 |
1826 |
1804 |
1781 |
|
1758 |
1736 |
|||
1,3 |
1714 |
|
1691 |
1669 |
1647 |
1626 |
1604 |
1582 |
1561 |
|
1539 |
1518 |
|||
1,4 |
1497 |
|
1476 |
1456 |
1635 |
1415 |
1394 |
1374 |
1354 |
|
1334 |
1315 |
|||
1,5 |
1295 |
|
1276 |
1257 |
1238 |
1219 |
1200 |
1182 |
1163 |
|
1145 |
1127 |
|||
1,6 |
1109 |
|
1092 |
1074 |
1057 |
1040 |
1023 |
1006 |
0989 |
|
0973 |
0957 |
|||
1,7 |
0940 |
|
0925 |
0909 |
0893 |
0878 |
0863 |
0848 |
0833 |
|
0818 |
0804 |
|||
1,8 |
0790 |
|
0775 |
0761 |
0748 |
0734 |
0721 |
0707 |
0694 |
|
0681 |
0669 |
|||
1,9 |
0656 |
|
0644 |
0632 |
0620 |
0608 |
0596 |
0584 |
0573 |
|
0562 |
0551 |
|||
2,0 |
0,0540 |
|
0529 |
0519 |
0508 |
0498 |
0488 |
0478 |
0468 |
|
0459 |
0449 |
|||
2,1 |
0440 |
|
0431 |
0422 |
0413 |
0404 |
0396 |
0387 |
0379 |
|
0371 |
0363 |
|||
2,2 |
0355 |
|
0347 |
0339 |
0332 |
0325 |
0317 |
0310 |
0303 |
|
0297 |
0290 |
|||
2,3 |
0283 |
|
0277 |
0270 |
0264 |
0258 |
0252 |
0246 |
0241 |
|
0235 |
0229 |
|||
2,4 |
0224 |
|
0219 |
0213 |
0208 |
0203 |
0198 |
0194 |
0189 |
|
0184 |
0180 |
|||
2,5 |
0175 |
|
0171 |
0167 |
0163 |
0158 |
0154 |
0151 |
0147 |
|
0143 |
0139 |
|||
2,6 |
0136 |
|
0132 |
0129 |
0126 |
0122 |
0119 |
0116 |
0113 |
|
0110 |
0107 |
|||
2,7 |
0104 |
|
0101 |
0099 |
0096 |
0093 |
0091 |
0088 |
0086 |
|
0084 |
0081 |
|||
2,8 |
0079 |
|
0077 |
0075 |
0073 |
0071 |
0069 |
0067 |
0065 |
|
0063 |
0061 |
|||
2,9 |
0060 |
|
0058 |
0056 |
005 |
0053 |
0051 |
0050 |
0048 |
|
0047 |
0046 |
|||
3,0 |
0,0044 |
|
0043 |
0042 |
0040 |
0039 |
0038 |
0037 |
0036 |
|
0035 |
0034 |
|||
3,1 |
0033 |
|
0032 |
0031 |
0030 |
0029 |
0028 |
0027 |
0026 |
|
0025 |
0025 |
|||
3,2 |
0024 |
|
0023 |
0022 |
0022 |
0021 |
0020 |
0020 |
0019 |
|
0018 |
0018 |
|||
3,3 |
0017 |
|
0017 |
0016 |
0016 |
0015 |
0015 |
0014 |
0014 |
|
0013 |
0013 |
|||
3,4 |
0012 |
|
0012 |
0012 |
0011 |
0011 |
0010 |
0010 |
0010 |
|
0009 |
0009 |
|||
3,5 |
0009 |
|
0008 |
0008 |
0008 |
0008 |
0007 |
0007 |
0007 |
|
0007 |
0006 |
|||
3,6 |
0006 |
|
0006 |
0006 |
0005 |
0005 |
0005 |
0005 |
0005 |
|
0005 |
0004 |
|||
3,7 |
0004 |
|
0004 |
0004 |
0004 |
0004 |
0004 |
0003 |
0003 |
|
0003 |
0003 |
|||
3,8 |
0003 |
|
0003 |
0003 |
0003 |
0003 |
0002 |
0002 |
0002 |
|
0002 |
0002 |
|||
3,9 |
0002 |
|
0002 |
0002 |
0002 |
0002 |
0002 |
0002 |
0002 |
|
0001 |
0001 |
|||
49
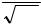
|
1 |
x |
|
z 2 |
|
2. Таблица значений функции Ф( х) = |
∫ |
||||
2π |
|||||
|
|
e 2 |
|||
|
|
0 |
|
|
|
dz .
х |
Ф(х) |
х |
Ф(х) |
х |
Ф(х) |
х |
Ф(х) |
Х |
Ф(х) |
0,00 |
0,0000 |
0,36 |
0,1406 |
0,72 |
0,2642 |
1,08 |
0,3599 |
1,44 |
0,4251 |
0,01 |
0,0040 |
0,37 |
0,1443 |
0,73 |
0,2673 |
1,09 |
0,3621 |
1,45 |
0,4265 |
0,02 |
0,0080 |
0,38 |
0,1480 |
0,74 |
0,2704 |
1,10 |
0,3643 |
1,46 |
0,4279 |
0,03 |
0,0120 |
0,39 |
0,1517 |
0,75 |
0,2734 |
1,11 |
0,3665 |
1,47 |
0,4292 |
0,04 |
0,0160 |
0,40 |
0,1554 |
0,76 |
0,2764 |
1,12 |
0,3686 |
1,48 |
0,4306 |
0,05 |
0,0199 |
0,41 |
0,1591 |
0,77 |
0,2794 |
1,13 |
0,3708 |
1,49 |
0,4319 |
0,06 |
0,0239 |
0,42 |
0,1628 |
078 |
0,2823 |
1,14 |
0,3729 |
1,50 |
0,4332 |
0,07 |
0,0279 |
0,43 |
0,1664 |
0,79 |
0,2852 |
1,15 |
0,3749 |
1,51 |
0,4345 |
0,08 |
0,0319 |
0,44 |
0,1700 |
0,80 |
0,2881 |
1,16 |
0,3770 |
1,52 |
0,4358 |
0,09 |
0,0359 |
0,45 |
0,1736 |
0,81 |
0,2910 |
1,17 |
0,3790 |
1,53 |
0,4370 |
0,10 |
0,0398 |
0,46 |
0,1772 |
0,82 |
0,2939 |
1,18 |
0,3810 |
1,54 |
0,4382 |
0,11 |
0,0438 |
0,47 |
0,1808 |
0,83 |
0,2967 |
1,19 |
0,3830 |
1,55 |
0,4394 |
0,12 |
0,0478 |
0,48 |
0,1844 |
0,84 |
0,2995 |
1,20 |
0,3849 |
1,56 |
0,4406 |
0,13 |
0,0517 |
0,49 |
0,1879 |
0,85 |
0,3023 |
1,21 |
0,3869 |
1,57 |
0,4418 |
0,14 |
0,0557 |
0,50 |
0,1915 |
0,86 |
0,3051 |
1,22 |
0,3888 |
1,58 |
0,4429 |
0,15 |
0,0596 |
0,51 |
0,1950 |
0,87 |
0,3079 |
1,23 |
0,3907 |
1,59 |
0,4441 |
0,16 |
0,0636 |
0,52 |
0,1985 |
0,88 |
0,3106 |
1,24 |
0,3925 |
1,60 |
0,4452 |
0,17 |
0,0675 |
0,53 |
0,2019 |
0,89 |
0,3133 |
1,25 |
0,3944 |
1,61 |
0,4463 |
0,18 |
0,0714 |
0,54 |
0,2 |
0,90 |
0,3159 |
1,26 |
0,3962 |
1,62 |
0,4474 |
0,19 |
0,0753 |
0,55 |
0,2088 |
0,91 |
0,3186 |
1,27 |
0,398 |
1,63 |
0,4484 |
0,20 |
0,0793 |
0,56 |
0,2123 |
0,92 |
0,3212 |
1,28 |
0,3997 |
1,64 |
0,4495 |
0,21 |
0,0832 |
0,57 |
0,2157 |
0,93 |
0,3238 |
1,29 |
0,4015 |
1,65 |
0,4505 |
0,22 |
0,0871 |
0,58 |
0,2190 |
0,94 |
0,3264 |
1,30 |
0,4032 |
1,66 |
0,4515 |
0,23 |
0,0910 |
0,59 |
0,2224 |
0,95 |
0,3289 |
1,31 |
0,4049 |
1,67 |
0,4525 |
0,24 |
0,0948 |
0,60 |
0,2557 |
0,96 |
0,3315 |
1,32 |
0,4066 |
1,68 |
0,4535 |
0,25 |
0,0987 |
0,61 |
0,2291 |
0,97 |
0,3340 |
1,33 |
0,4082 |
1,96 |
0,4545 |
0,26 |
0,1026 |
0,62 |
0,2324 |
0,98 |
0,3365 |
1,34 |
0,4099 |
1,70 |
0,4554 |
0,27 |
0,1064 |
0,63 |
0,2357 |
0,99 |
0,3389 |
1,35 |
0,4115 |
1,71 |
0,4564 |
0,28 |
0,1103 |
0,64 |
0,2389 |
1,00 |
0,3413 |
1,36 |
0,4131 |
1,72 |
0,4573 |
0,29 |
0,1141 |
0,65 |
0,2422 |
1,01 |
0,3438 |
1,37 |
0,4147 |
1,73 |
0,4582 |
0,30 |
0,1179 |
0,66 |
0,2454 |
1,02 |
0,3461 |
1,38 |
0,4162 |
1,74 |
0,4591 |
0,31 |
0,1217 |
0,67 |
0,2486 |
1,03 |
0,3485 |
1,39 |
0,4177 |
1,75 |
0,4599 |
0,32 |
0,1255 |
0,68 |
0,2517 |
1,04 |
0,3508 |
1,40 |
0,4192 |
1,76 |
0,4608 |
0,33 |
0,1293 |
0,69 |
0,2549 |
1,05 |
0,3531 |
1,41 |
0,4207 |
1,77 |
0,4616 |
0,34 |
0,1331 |
0,70 |
0,2580 |
1,06 |
0,3554 |
1,42 |
0,4222 |
1,78 |
0,4625 |
0,35 |
0,1368 |
0,71 |
0,2611 |
1,07 |
0,3577 |
1,43 |
0,4236 |
1,79 |
0,4633 |
1,80 |
0,4641 |
1,96 |
0,475 |
2,24 |
0,4875 |
2,56 |
0,4948 |
2,88 |
0,4980 |
1,81 |
0,4649 |
1,97 |
0,4756 |
2,26 |
0,4881 |
2,58 |
0,4951 |
2,90 |
0,4981 |
1,82 |
0,4656 |
1,98 |
0,4761 |
2,28 |
0,4887 |
2,60 |
0,4953 |
2,92 |
0,4982 |
1,83 |
0,4664 |
1,99 |
0,4767 |
2,30 |
04893 |
2,62 |
0,4956 |
2,94 |
0,4984 |
1,84 |
0,4671 |
2,00 |
0,4772 |
2,32 |
0,4898 |
2,64 |
0,4959 |
2,96 |
0,4985 |
1,85 |
0,4678 |
2,02 |
0,4783 |
2,34 |
0,4904 |
2,66 |
0,4961 |
2,98 |
0,4986 |
1,86 |
0,4686 |
2,04 |
0,4793 |
2,36 |
0,4909 |
2,68 |
0,4963 |
3,00 |
0,49865 |
1,87 |
0,4693 |
2,06 |
0,4803 |
2,38 |
0,4913 |
2,70 |
0,4965 |
3,20 |
0,49931 |
1,88 |
0,4699 |
2,08 |
0,4812 |
2,40 |
0,4918 |
2,72 |
0,4967 |
3,40 |
0,49966 |
1,89 |
0,4706 |
2,10 |
0,4821 |
2,42 |
0,4922 |
2,74 |
0,4969 |
3,60 |
0,499841 |
1,90 |
0,4713 |
2,12 |
0,4830 |
2,44 |
0,4927 |
2,76 |
0,4971 |
3,80 |
0,499928 |
1,91 |
0,4719 |
2,14 |
0,4838 |
2,46 |
0,4931 |
2,78 |
0,4973 |
4,00 |
0499968 |
1,92 |
0,4726 |
2,16 |
0,4846 |
2,48 |
0,4934 |
2,80 |
0,4974 |
4,50 |
0,499997 |
1,93 |
0,4732 |
2,18 |
0,4854 |
2,50 |
0,4938 |
2,82 |
0,4976 |
5,00 |
0,499997 |
1,94 |
0,4738 |
2,20 |
0,4861 |
2,52 |
0,4941 |
2,84 |
0,4977 |
|
|
1,95 |
0,4744 |
2,22 |
0,4868 |
2,54 |
|
2,86 |
0,4979 |
|
|
50
