4166_27v-IDZ9

ИДЗ 9.1 – Вариант 27

1. Вычислить определенные интегралы с точностью до двух знаков после запятой.

1.27

Если функция y=f(x) непрерывна на отрезке [a,b] и F(x) – любая первообразная той функции на [a,b], то определенный интеграл от функции f(x) на [a,b] равен приращению первообразной на этом отрезке:

Положим , тогда .

Если x=, то ; если x=, то

Поэтому:

2.27

Сделаем замену ,

при при

Тогда

Сделаем замену и

при при

Решение интеграла:

3.27

Если функция y=f(x) непрерывна на отрезке [a,b] и F(x) – любая первообразная той функции на [a,b], то определенный интеграл от функции f(x) на [a,b] равен приращению первообразной на этом отрезке:

Представим

Тогда интеграл

4.27

Сделаем замену ,

Тогда 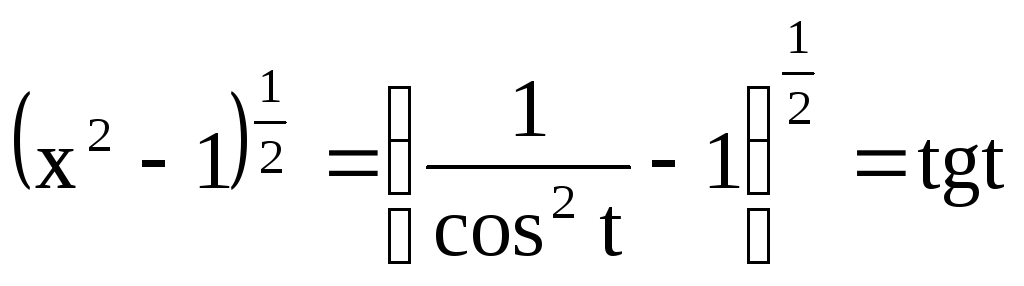и при ,

Вычислим интеграл

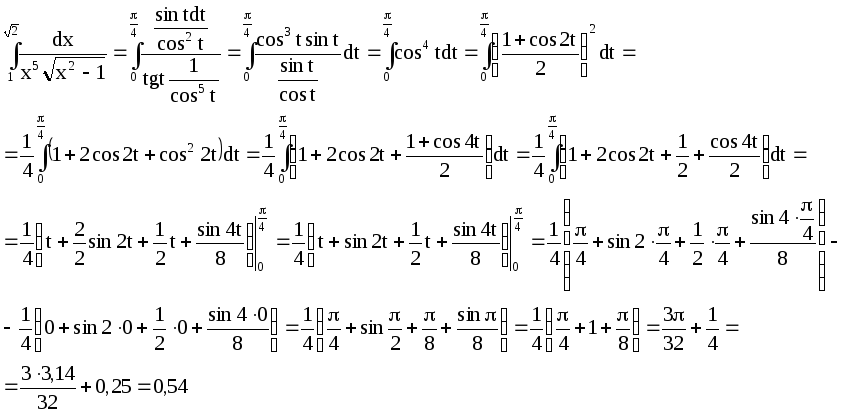
5.27

Согласно тригонометрическому тождеству

Получаем:

Сделаем замену ,

при ,

Тогда

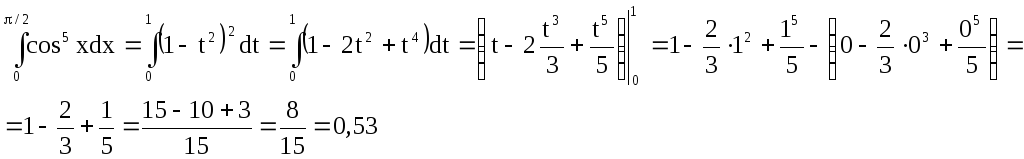
6.27

Представим знаменатель интеграла в виде квадрата суммы:

Табличная формула интегрирования

Подставляем, получаем:

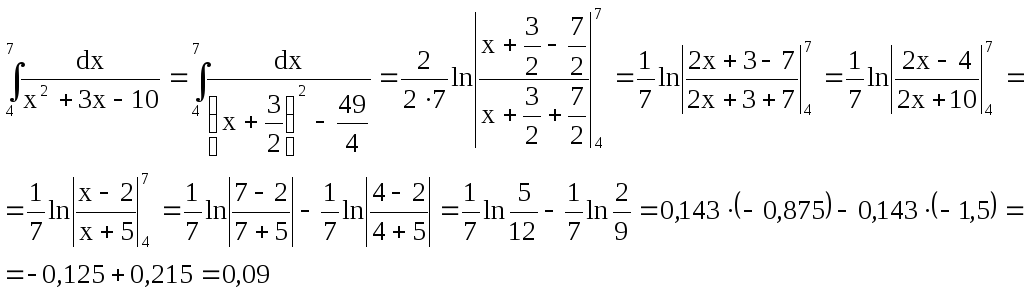
7.27

Сделаем замену ,

при при

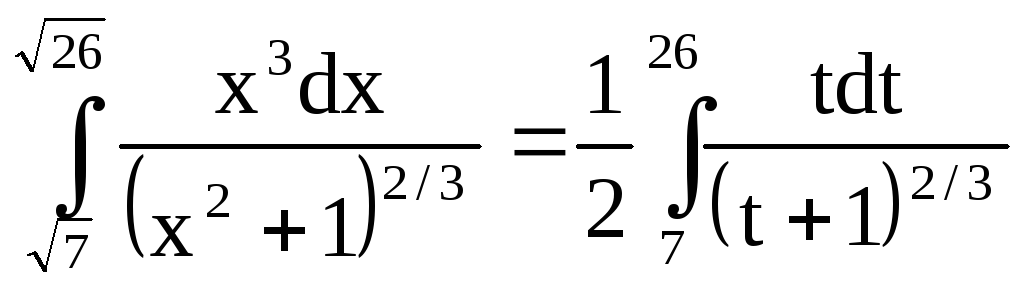
Сделаем замену ,

при при

8 Вычислить несобственные интегралы или доказать их расходимость:

8.27 а)

Несобственный интеграл с бесконечными пределами интегрирования (1 рода)

от функции y=f(x) на полуинтервале называется предел функции Ф(t) при

Если такой предел существует и конечен, то несобственный интеграл называется сходящимся к данному пределу. Если конечного предела не существует, то несобственный интеграл называется расходящимся.

Найдем неопределенный интеграл?

Сделаем замену отсюда

Получаем:

Возвратившись к старой переменной, имеем

Окончательно получаем:

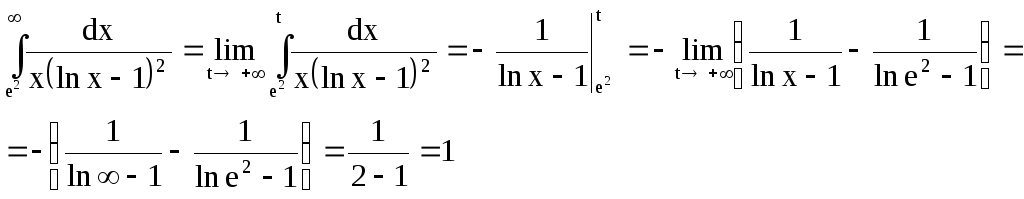
б)

Если функция f(x) непрерывна при a < x ≤ b и имеет точку разрыва x = a, тогда

Подынтегральная функция терпит бесконечный разрыв в точке . Следовательно, по определению

Решим интеграл:

Представим знаменатель интеграла в виде квадрата разности:

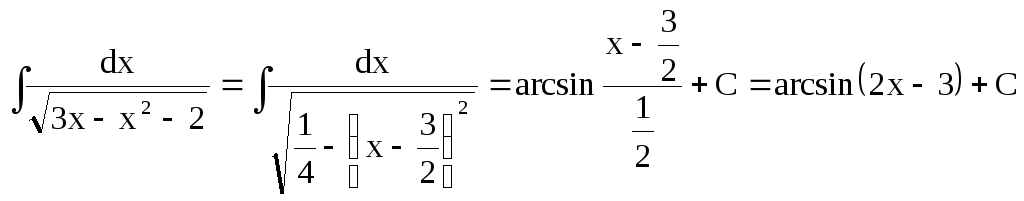
Тогда: