
- •Московский государственный университет информационных технологий, радиотехники и электроники
- •Институт высоких технологий
- •Москва - 2015
- •Введение
- •Общие методические указания
- •Инструкция по технике безопасности в лаборатории Общие требования безопасности
- •Требования безопасности во время занятий
- •Лабораторная работа № 1
- •Исследование эффективности методов
- •Разделения воздуха
- •История получения газов путем разделения воздуха
- •Теория воздухоразделения
- •1, 2-Ректификац. Колонны; 3 - конденсатор-испаритель
- •1. 2-Соотв. Нижняя и верхняя ректификац. Колонны, 3-дополнит, колонна, 4-конденсатор; б-блок выделения азота, где 1-ректификац. Колонна, 2 - конденсатор
- •Принцип разделения воздуха
- •Лабораторная работа №2
- •Опорожнения резервуара для хранения криогенных жидкостей
- •1. Цель работы
- •2. Конструкции цистерн для криогенных жидкостей
- •3. Принципиальная схема цистерны цтк- 1,6/0,25
- •4. Порядок работы
- •4.1. Наполнение цистерны
- •4.2. Опорожнение цистерны
- •5. Указание мер безопасности
- •6. Отчет по лабораторной работе
- •Лабораторная работа № 3
- •2. Схема стенда
- •3. Теоретические положения. Определение объема жидкости и поверхности контакта Сферический сосуд
- •Цилиндрический сосуд с эллиптическими днищами
- •4. Методика эксперимента
- •5. Обработка результатов эксперимента
- •12. Оформить протокол лабораторной работы. Протокол оформляется индивидуально каждым студентом. Протокол должен содержать пояснения выполняемых действий.
- •6. Приложения
- •Лабораторная работа №1 «исследование теоретического и действительного циклов газовой криогенной машины»
- •Общие теоретические| положения|
- •Принципиальная схема и цикл идеальной гкм
- •Цикл гкм с гармоническим движением поршней
- •2.Конструкция газовой криогенной машины
- •3. Ход работы
- •4. Обработка результатов измерений
- •Литература
2. Схема стенда
Стенд для проведения испытаний состоит из сосуда Дьюара 1 сферической или цилиндрической формы, в который заливается заданное количество жидкого азота. Азот выбран в качестве испытуемой криогенной жидкости по условиям его инертности и негоючести.
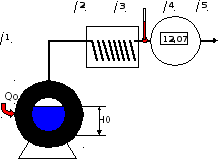
Рис. 2.1. Схема стенда для проведения работы
Испаряющиеся пары азота по трубопроводу 2 отводятся в змеевик сосуда 3. Этот сосуд заполнен водой и служит для нагрева паров азота до комнатной температуры перед их поступлением в счетчик расхода 5. Температура паров поступающих на счетчик контролируется термометром 4.
3. Теоретические положения. Определение объема жидкости и поверхности контакта Сферический сосуд

Для сферического сосуда должен быть известен диаметр внутренней полости Dc и уровень жидкости Н.
Радиус сферы Rc = Dc/2
Полная поверхность
сферы
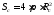 .
.
Полный объем сферы
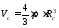 .
.
При заполнении емкости на высоту Н образуется шаровой сегмент, заполненный жидкостью.
Радиус этого сегмента
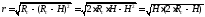 .
.
Смоченная жидкостью поверхность сосуда есть боковая поверхность шарового сегмента
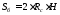 .
(2.1)
.
(2.1)
Объем жидкости в сферическом сегменте
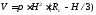 .
(2.2)
.
(2.2)
Цилиндрический сосуд с эллиптическими днищами
Объем, занимаемый
жидкостью,
состоит из 2-ух частей: цилиндрического
объема высотой Н–Нэ
и объема эллиптического днища. Стандартное
эллиптическое днище имеет высоту равную
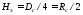 .
.
Объем жидкости в цилиндрической части
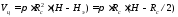 .
(2.3)
.
(2.3)
Объем
эллиптического днища можно определить
следующим образом. Выделим тонкий слой
высотой dz.
Его объем равен
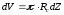 .
МеждуR
и Z
существует связь
.
МеждуR
и Z
существует связь
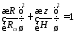 или
или
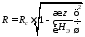 .
.
Объем днища определяется интегрированием
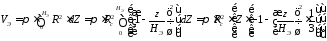 .
.
При полном заполнении днища Z = HЭ
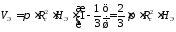 ,
,
с учетом
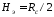 получим
получим
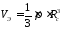 .
(2.4)
.
(2.4)
При
неполном заполнении объема днища
 ,
объем нижнего сегмента равен
,
объем нижнего сегмента равен
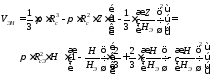 (2.5)
(2.5)
Составим таблицу объемов при неполном заполнении
Поверхность эллиптического сегмента может быть вычислена из соотношения для поверхности тонкого слоя высотой dZ.
 .
.
Используем уравнение
связи R
и Z
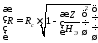 ,
получим
,
получим
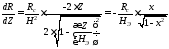 где
где
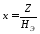 .
.
Поверхность верхней части сегмента высотой Z равна
 .
.
Здесь учтено, что
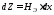 .
.
После преобразований получим
 ,
где
,
где
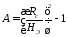 .
.
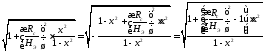 .
.
Введем
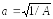 и получим табличный интеграл
и получим табличный интеграл
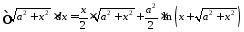 .
.
Соответственно
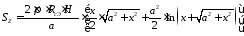 .
(2.6)
.
(2.6)
Поверхность днища получится при х=1
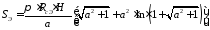
Для
стандартного днища
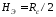 и
и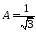 тогда полная поверхность днища
тогда полная поверхность днища
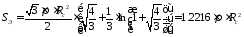 .
(3.7)
.
(3.7)
Поверхность нижнего
(заполненного жидкостью) сегмента равна
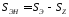 . (2.8)
. (2.8)
Составим таблицу.
Влияние паровой части стенки на теплопритоки к жидкости
Выделим элемент стенки, высотой dZ.
При диаметре Dc теплоприток извне равен
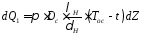 , где t
- температура
стенки.
, где t
- температура
стенки.
Отвод тепла к пару
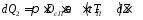
Теплоприток сверху по стенке
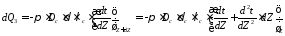 .
.
Теплоотвод снизу по стенке
 .
.
Составим тепловой баланс элемента
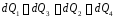 или
или
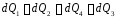
 .
.
После сокращений и приведения подобных получим дифференциальное уравнение
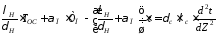 ,
или в классическом виде
,
или в классическом виде
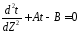 .
.
где
 ;
;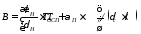
Для упрощения
задачи примем допущения, что теплофизические
свойства
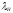 и
и не зависят от температуры, т.е. постоянны.
Второе допущение состоит в том, что
не зависят от температуры, т.е. постоянны.
Второе допущение состоит в том, что не меняется и равна
не меняется и равна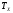 .
Это означает, что А и В =const.
.
Это означает, что А и В =const.
При принятых условиях задача сводится к задаче о температурном поле ребра постоянной толщины, находящегося в среде с постоянной эквивалентной температурой
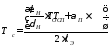 и
и
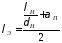 .
.
Используя решение, полученное для ребра постоянной толщины, получим соотношение для температурного поля
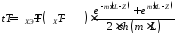 .
.
Где L –высота стенки.
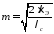 -
тепловой параметр ребра.
-
тепловой параметр ребра.
Количество тепла, которое поступает по стенке к жидкости
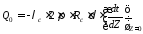
При высоте стенки L
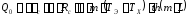 .
(2.9)
.
(2.9)
Аналогичное соотношение при бесконечной высоте стенки имеет вид
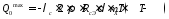 .
(2.10)
.
(2.10)
Составим таблицу.
