Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Московский государственный университет приборостроения и информатики

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

metod_fmp

.pdf

Скачиваний:

Добавлен:

15.03.2016

Размер:

756.7 Кб

Скачать

☆

<<< < Предыдущая 12 / 42 3 4 > Следующая >>>

∂z dx

∂z dy

+ ∂z

∂x dt

∂y dt

∂t

2(x

)

−sin

+ y

e4t 4

−sin

+ y

6 y

2 +sin

+ y

cos

Задача 8.

Найти

, если z = arctg(x 4 y 2t 5 ), где x = sin 3t ,

y = e2t .

′

(Напомним (arctgx)

1 + x2

∂z

∂

[arctg(x 4 y 2t 5 )]=

1 + (x 4 y 2 t 5 )2

∂x

y 2 t 5 4x3 =

4x3 y 2 t 5

+ x8 y 4 t10

∂z

∂

[arctg(x 4 y 2t 5 )]=

1 + (x 4 y 2 t 5 )2

∂y

x 4 t 5 2 y =

2x 4 yt 5

+ x8 y 4 t10

∂z

∂

[arctg(x 4 y 2 t 5 )]=

∂t

1 + (x 4 y 2t 5 )2

x 4 y 2 5t 4 =

5x 4 y 2 t 4

+ x8 y 4 t10

dxdt = dtd (sin 3t )= 3cos 3t . dydt = dtd (e2t )= e2t 2 .

∂	(x 4 y 2 t 5 )=	1	y 2 t 5	∂	(x 4 ) =
∂x		1 + x8 y 4 t10		∂x

∂	(x 4 y 2 t 5 )=	1	x 4t 5	∂	( y 2 ) =
∂y		1 + x8 y 4 t10		∂y

∂	(x 4 y 2t 5 )=	1	x 4 y 2 t 5	∂	(t 5 ) =
∂t		1 + x8 y 4 t10		∂t

Тогда

∂z dx

∂z dy

∂z

4x3 y 2 t 5

3cos 3t +

2x 4 yt 5

e2t 2 +

5x 4 y 2 t 4

∂x dt

∂y dt

∂t

+ x8 y 4 t10

+ x8 y 4t10

+ x8 y 4 t10

В процессе решения следующих задач используется понятие производной по направлению. Напомним суть этого понятия. Пусть имеется

функция трех переменных

u = u(x; y; z) и

некоторая точка пространства

M 0 (x0 ; y0 ; z0 ) .

Производной

∂u

точке

M 0 в

направлении вектора a

∂s

называется следующий предел

∂u = lim

u(x0

+ x; y0 +

y; z0 +

z) −u(x0 ; y0 ; z0 )

где

длина вектора M 0 M1 ,

∂s

s→0

соединяющего точки

M 0 (x0 ; y0 ; z0 )

M1 (x0 + x; y0

y; z0 + z) , при этом сам

вектор

M 0 M1

параллелен вектору

и имеет с этим вектором одинаковое

направление. Производная по направлению характеризует скорость изменения функции в направлении вектора a . При вычислении производной по направлению удобно использовать понятие градиента функции.

Градиентом функции u = u(x; y; z)					называется вектор,		обозначаемый
grad(u),		который		определяется	следующими	соотношениями
grad(u)=	∂u	∂u	∂u			G
grad(u)=	∂x	; ∂y ;	∂z . Производная по направлению вектора			a	равна проекции

градиента функции на это направление. Таким образом, можно сказать, что

grad(u) направлен в направлении наиболее быстрого возрастания функции, а
его модуль равен скорости роста в этом направлении.							G
Напомним формулу проекции вектора			a на вектор				G	, которая
Напомним формулу проекции вектора			a на вектор				b	, которая
				G
изучалась в курсе аналитической геометрии прbGaG			=	(aGb	)	, где (aGb)	-	скалярное
				b
произведение векторов aG и b ,	b	- модуль вектора b . Напомним,						что если в
произведение векторов aG и b ,	b	- модуль вектора b . Напомним,						что если в

прямоугольной декартовой системе координат координаты векторов a и b

соответственно

равны a = {X1 ;Y1 ; Z1 },

b ={X 2 ;Y2 ; Z2 },

то

их скалярное

произведение вычисляется по формуле (aGb) = X1 X 2

+Y1Y2 + Z1Z2 .

Следовательно,

если координаты

вектора

соответственно

равны

aG={ax ; ay ; az },

то

производная по направлению

вектора

aGвычисляется по

формуле

∂u

∂u a

+ ∂u a

∂x

∂y

∂z

∂s

ax 2 + ay 2 + az 2

Задача 9.

Дана функция u = x2 y + y2 z + z 2 x .

Найти: а) градиент

функции; б) производную

по

направлению

вектора

aG = {2;−1;2} в точке М(3;1;2).

Найдем градиент u .

grad(u)= ∂u ;

∂u ;

∂u

. Вычислим частные производные.

∂x

∂y

∂z

∂u	=	∂	(x2 y + y2 z + z 2 x)= 2xy + z 2 .
∂x		∂x

∂u	=	∂	(x2 y + y2 z + z 2 x)= x2 + 2 yz .
∂y		∂y

∂u	=	∂	(x2 y + y2 z + z2 x)= y2 + 2zx .
∂z		∂z

Тогда

grad(u)={2xy + z 2 ; x2 + 2 yz; y2 + 2zx}.

Полагая x=3, y=1, z=2, получаем grad(u)={10;13;13}.

Используя формулу

∂u

(gradu a)

, получаем

∂u

10 2 +13 (−1) +13 2

=11.

∂s

22 +(−1)2 + 22

В следующей

задаче изучаются методы построения касательной

плоскости и нормали к поверхности. Напомним основные моменты

теоретического						курса. Если	поверхность определяется уравнением
Φ(x; y; z) = 0 ,					и точка M 0 (x0 ; y0 ; z0 )		лежит на указанной поверхности, то вектор
G	∂Φ		∂Φ		∂Φ	, вычисленный	в точке M 0 (x0 ; y0 ; z0 ) перпендикулярен
N =		;		;
	∂x		∂y		∂z

касательной плоскости к поверхности. Тогда уравнение касательной плоскости может быть записано в виде

∂Φ	(x − x0 ) +	∂Φ	( y − y0 ) +	∂Φ	(z − z0 ) = 0 .
∂x		∂y		∂z

Уравнение нормали, записанное в каноническом виде, определяется соотношениями

x − x0 = y − y0

∂Φ ∂Φ ∂x ∂y

= z∂−Φz0 . ∂z

Задача 10. Найти уравнение касательной плоскости и нормали к поверхности xy2 + yz2 + xyz − 28 = 0 в точке М(1;2;3).

Имеем:

∂∂Φx = ∂∂x (xy2 + yz2 + xyz −28)= y2 + yz =10 ;

∂∂Φy = ∂∂y (xy2 + yz2 + xyz − 28)= 2xy + z 2 + xz =16 ;

∂∂Φz = ∂∂z (xy2 + yz2 + xyz − 28)= 2 yz + xy =14 .

Тогда уравнение касательной плоскости имеет вид

10(x-1)+16(y-2)+14(z-3)=0.

Преобразуя это уравнение, получаем окончательный вид

5x+8y+7z-42=0.

Каноническое уравнение нормали имеет вид

x10−1 = y16−2 = z14−3

Теперь рассмотрим задачи, связанные с применением полного дифференциала в приближенных вычислениях. Суть этого состоит в приближенной замене полного приращения функции ее полным дифференциалом. (Напомним, что полный дифференциал dz функции двух

переменных z(x; y) равен dz =	∂z dx +		∂z	dy ).		Для приближенных вычислений

	∂x		∂y
применяется формула		∂z			∂z
z(x + x; y + y) ≈ z(x; y) + dz = z(x; y) +			x +			y .
		∂x			∂y

Рассмотрим пример применения данной формулы.

Задача 11. Вычислить приближенно с помощью дифференциала первого порядка 4,022 + 2,972 .

Рассмотрим функцию z(x; y) = x2 + y2 . В указанном примере требуется вычислить значение функции в точке M1 (x1 ; y1 ) , координаты которой соответственно равны x1 = 4,02 , y1 = 2,97 .

Рассмотрим близкую точку M 0 (x0 ; y0 ) , в которой вычисление функции не представляет проблему. В качестве такой точки возьмем

M 0 (4;3) , то есть x0

= 4 ,

= 3 . Тогда

x = 4,02 − 4 = 0,02 ,

y = 2,97 −3 = −0,03.

Имеем z(x + x; y +

y) ≈ z(x; y) + dz = z(x; y) +

∂z

x +

∂z

y . Поскольку

∂x

∂y

z(x; y) = x2 + y2 , то ∂z

∂z

∂y

∂x

x2 + y2

Тогда

(x0 + x)2 + ( y0 + y)2 ≈ x0 2 + y0 2 +

x +

y .

x0 2 + y0 2

Поскольку x0 = 4 ,

y0 = 3 ,

x = 0,02 ,

y = −0,03 ,

то

4,022 + 2,972 =

(4 + 0,02)2 + (3 −0,03)2

≈

42 +32

0,02 +

(−0,03) =

+32

0,08 − 0,09

=5+

= 4,998.

Далее ознакомимся с методами вычисления полных дифференциалов

высших порядков. Общее правило для			вычисления		d n z - полного
дифференциала порядка n выглядит следующим образом
d n z = d(d n−1 z) .
Напомним, что полный дифференциал первого порядка определяется
соотношением dz = ∂z dx +	∂z	dy .
соотношением dz = ∂z dx +		dy .
∂x	∂y
			x
Задача 12. Найти d 2 z , если z = x sin			x	.
Задача 12. Найти d 2 z , если z = x sin				.

			y

Согласно приведенной выше формуле полный дифференциал

второго порядка равен полному дифференциалу от полного дифференциала первого порядка.

Найдем полный дифференциал первого порядка.

∂

dz =

xsin

dx +

x sin

dy = sin

cos

dx + −

cos

∂x

∂y

Далее найдем полный дифференциал второго порядка

d 2 z = d(dz) =

∂

(dz)dx +

∂

(dz)dy =

∂x

∂y

∂

sin

cos

dx +

−

cos

dy dx +

∂x

∂

sin

cos

dx +

−

cos

dy dy =

∂y

dx +

cos

−

sin

dx +

−

cos

sin

x x

−

cos

sin

−

cos

sin

dx +

cos

−

sin

dy dy .

Группируя слагаемые, получаем

z =

cos

−

sin

+ 2

−

cos

−

sin

dy2 .

dxdy +

cos

sin

Далее ознакомимся с методами исследования функции двух переменных на экстремум. Напомним некоторые основные моменты теории.

Пусть имеется функция двух переменных z = z(x; y) . Точками экстремума могут являться только такие точки, в которых частные производные ∂∂xz и ∂∂yz

или равны нулю или не существуют. Такие точки плоскости будем называть критическими. Следовательно, для определения критических точек имеем систему двух уравнений с двумя неизвестными вида

		∂z	= 0;
		∂x	= 0;
		∂x
		∂z
		∂z	= 0.
			= 0.
		∂y
		∂y

Однако указанные условия не являются достаточными условиями экстремума. Для проверки, является ли критическая точка точкой экстремума, используется следующая схема. Обозначим через А, В, С следующие значения вторых производных, вычисленных в критической точке:

A =	∂2 z	; B =	∂2 z	; C =	∂2 z .
	∂x2		∂x∂y
					∂y2

Тогда:

1. Если AC − B2 > 0 , то исследуемая критическая точка является точкой экстремума и

вслучае A > 0 - исследуемая точка является точкой минимума

вслучае A < 0 - исследуемая точка является точкой максимума;

2.Если AC _ B2 < 0 , то исследуемая точка не является точкой экстремума.

3.Если AC − B2 = 0 , то данный метод ответа на поставленный вопрос не дает и требуется привлекать другие методы.

Задача 12. Исследовать на экстремум функцию z = x3 + y3 −3xy .

Вычислим частные производные.

∂z

= 3x2

−3y .

∂x

∂z

= 3y2

−3x .

∂y

Для определения критических точек имеем систему уравнений

−3y = 0;

−3x = 0.

Решим эту систему

−3y

− y = 0;

= y;

= x x(x3 −1) = 0 .

−3x

− x = 0.

= x.

Полученное уравнение для	неизвестной x имеет два корня	x1 = 0, x2 =1.
Поскольку y = x2 , то y1 = 0, y2	=1.
Следовательно, критическими являются две точки плоскости M1 (0;0)		и M 2 (1;1) .

Определим, являются ли эти точки точками экстремума. Для этого вычислим вторые производные.

∂2 z

∂

(3x2 −3y) = 6x .

∂x2

∂x

∂2 z

∂

(3x2 −3y) = −3.

∂x∂y

∂y

∂2 z

∂

(3y2 −3x) = 6 y .

∂y2

∂y

Исследуем первую точку M1 (0;0) .

A =

∂2 z = 6 0 = 0 , B =

∂2 z

= −3 , C =

∂2 z

= 6 0 = 0 .

∂x∂y

∂y2

∂x2

Тогда AC − B2 = −9 < 0 , следовательно, M1 (0;0) не является точкой экстремума. Исследуем вторую точку M 2 (1;1) .

A = ∂2 z

= 6 1 = 6 , B =

∂2 z

= −3 , C = ∂2 z = 6 1 = 6 .

∂x∂y

∂x2

∂y2

Тогда

AC − B2 = 27 > 0 ,

следовательно,

M 2 (1;1) является точкой

экстремума.

Поскольку А=6>0, то эта точка является точкой минимума.

Задача 14. Исследовать на экстремум функцию z = −x2 + xy − 2 y2

+3x + 2 y .

Вычислим частные производные.

∂z

= −2x + y +3 .

∂x

∂z

= x − 4 y + 2 .

∂y

Для определения критических точек имеем систему уравнений

− 2x + y +3 = 0,

2x − y = 3,

− 4 y + 2 = 0.

x − 4 y = −2.

Используя формулы Крамера, получаем

−1

= −7 ,

x =

−1

= −14 ,

− 4

− 2

− 4


y =		2	3		= −7 , x = x = 2 ,
		1	− 2
является точка М(2;1).
A =	∂2 z		=	∂		(−2x + y +3) = −2 ,
	∂x2			∂x

C =	∂2 z		=	∂		(x − 4 y + 2) = −4 .
	∂y2			∂y

y =	y	=1. Следовательно,	критической точкой

		B =	∂2 z	=	∂	(−2x + y +3) =1,
			∂x∂y		∂y

Тогда AC − B2 = 7 > 0 , следовательно, M (2;1) является точкой экстремума. Поскольку A = −2 < 0 , то эта точка является точкой максимума.

Некоторые задачи связаны с нахождением условного экстремума функции и нахождению наибольшего и наименьшего значений функции в замкнутой ограниченной области.

Начнем с рассмотрения задачи условного экстремума.

Пусть имеется функция двух переменных z = f (x; y) . Требуется определить точки экстремума этой функции при условии, что переменные x и y не являются независимыми, а связаны соотношением ϕ(x : y) = 0 . Фактически это означает, что мы исследуем функцию z = f (x; y) не на всей плоскости, а на некоторой линии, лежащей на этой плоскости.

Для решения этой задачи используется метод множителей Лагранжа. Введем функцию трех переменных F(x; y;λ) следующим образом

F(x; y;λ) = f (x; y) + λϕ(x; y) . (λ – называют множителем Лагранжа). Тогда точки экстремума определяются из решения системы трех уравнений с тремя неизвестными x, y, λ вида:

∂∂Fx = 0,

∂∂Fy = 0,

∂∂Fλ = 0.

Задача 15. Найти условный экстремум функции z = x2 + xy + y2 , если x2 + y2 = 4 .

Прежде чем составить выражение для функции Лагранжа, уравнение связи между переменными x и y перепишем в виде x2 + y2 − 4 = 0 .

Тогда выражение для функции Лагранжа имеет вид

F(x; y;λ) = x2

Из условия

+ xy + y2 + λ(x2 + y2 − 4).
	∂F	= 0,
	∂F	= 0,
	∂x	2x + y
	∂F
		= 0, получаем систему уравнений x	+ 2 y
	∂y	= 0, получаем систему уравнений x	+ 2 y
	∂y		2
	∂F	x		+ y
		= 0.
	∂λ	= 0.
	∂λ

+2λx = 0,

+2λy = 0,

2 −4 = 0.

Первые два уравнения системы перепишем в виде 2(1 + λ)x + y = 0,	,	и будем
x + 2(1 + λ) y = 0.		x и y .
рассматривать как систему двух уравнений с двумя неизвестными		x и y .

Данная система является однородной системой двух линейных уравнений с двумя неизвестными. Она всегда допускает нулевое решение. Ненулевое решение такой системы существует только тогда, когда определитель системы равен нулю. Условие равенства нулю определителя системы дает уравнение для определения λ .

Имеем

2(1 + λ)

= 0 . Вычисляя определитель,

получаем уравнение

2(1 + λ)

4(1 + λ)2

−1 = 0 . Это уравнение имеет два корня λ1

= −

и λ2

= −

Рассмотрим

вначале

λ1

= −

Подставляя

первое

уравнение

системы,

получаем 2x + y + 2λx = 0 , 2x + y + 2 −

x = 0 ,

x + y = 0

y = −x .

Тогда из последнего уравнения системы следует: x2

+ y2

− 4 = 0 ;

x2 + (−x)2 − 4 = 0 ;

2x2 = 4 ;

x1 =

2, x2 = −

2 .

Из

условия

y = −x

находим

y1 = −

2, y2 =

2 .

Следовательно,

значению

λ1 = −

соответствуют

две

точки

плоскости

M1 ( 2;− 2) и M2 (− 2; 2) .

Аналогично

рассмотрим

λ2

= −

Из первого

уравнения

системы

следует

2x + y + 2λx = 0 ,

2x + y +

−

x = 0 ,

− x + y = 0 ,

y = x .

Тогда

из последнего

уравнения

системы

следует:

x2 + y2 − 4 = 0 ;

x2 + (x)2

− 4 = 0 ;

2x2 = 4 ;

x3 = 2, x4

= −

2 .

Из

условия

y = x

находим

2, y4

= − 2 .

Следовательно,

значению

λ2

= −

соответствуют

две

точки

плоскости

M3 (

M4 (− 2;− 2).

Вычислим значения функции в этих точках.

M1 ( 2;− 2). f (x; y) = ( 2)2 + 2 (− 2) +(− 2)2 = 2 . M2 (− 2; 2) . f (x; y) = (− 2)2 +(− 2) ( 2) +( 2)2 = 2 . M3 ( 2; 2). f (x; y) = ( 2)2 +( 2) ( 2) +( 2)2 = 6 .

M4 (− 2;− 2). f (x; y) = (− 2)2 +(− 2) (− 2) +(− 2)2 = 6 .

Следовательно, точки M1 ( 2;− 2) и M2 (− 2; 2) являются точками минимума, а точки M3 ( 2; 2) и M4 (− 2;− 2) - являются точками максимума.

Далее рассмотрим задачу нахождения наибольшего и наименьшего значений функции в замкнутой ограниченной области. Известно, что непрерывная функция в замкнутой ограниченной области принимает свое наибольшее и наименьшее значения. Если соответствующая точка лежит внутри области, то такая точка является точкой экстремума. Если такая точка лежит на границе, то она является точкой условного экстремума. Тогда можно предложить следующую схему.

1.Находим критические точки, лежащие внутри области. 2.Находим точки условного экстремума, лежащие на границе.

3.Вычисляем значения функции в найденных точках, и определяем наибольшее

инаименьшее значения.

			20
Задача 16.		Найти	наибольшее	и наименьшее значения функции
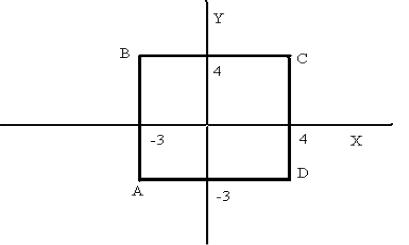
z = 3x2	+ 2xy + 2 y2	+10x +10 y	в области,	ограниченной линиями: x = −3 , y = −3 ,
x = 4 ,	y = 4 .

Схематично область изображена на рисунке.

1. Найдем точки экстремума функции.

Из условия ∂z

= 0 ,

∂z

= 0 получаем систему уравнений.

∂x

∂y

6x + 2 y +10 = 0,

6x + 2 y = −10,

+10 = 0.

2x + 4 y

2x + 4 y = −10.

Решаем эту систему.

= 20 ,

x =

−10

= −20 ,

y =

−10

= −40 , x = −1,

−10

y = −2 .

Найденная

точка

M1 (−1,−2)

лежит

внутри

области,

поэтому она

находится среди точек, в которых может достигаться наибольшее или наименьшее значения.

2. Далее исследуем границу области. Она состоит из четырех линий, каждую из которых исследуем отдельно.

Линия АВ. Ее уравнение							x = −3 или	x +3 = 0 .	(Заметим, что −3 ≤ y ≤ 4 ).
Составляем функцию Лагранжа.
F(x; y;λ) = 3x2 + 2xy + 2 y2 +10x +10 y +λ( x +3 ).
Из условия	∂F	= 0,	∂F	= 0,	∂F	= 0	получаем	систему	трех уравнений с тремя
	∂x		∂y
					∂λ

неизвестными

6x + 2 y +10 + λ = 0,2x + 4 y +10 = 0,

x +3 = 0.

Найдем x и y . Из последнего уравнения системы следует x = −3 . Тогда из второго уравнения следует y = −1. Точка M 2 (−3;−1) лежит на линии АВ, поэтому

она ходит в число тех точек, в которых может достигаться наибольшее или наименьшее значения. Кроме того, наибольшее или наименьшее значения могут достигаться на границах линии АВ. Поэтому в число возможных точек

<<< < Предыдущая 12 / 42 3 4 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
09.04.20151.42 Mб115Metodichka_2005_Excel_Word_i_Kurs_rabota_2 (3).doc
#
15.03.2016940.08 Кб7Metodichka_po_D_R_1_1_5_int.docx
#
17.12.20181.61 Mб4metodichka_po_matematike_dlja_pz.docx
#
09.04.2015803.84 Кб171Metodichka_по англ.doc
#
09.04.2015297.98 Кб6Metodich_ukazania_1.doc
#
15.03.2016756.7 Кб8metod_fmp.pdf
#
15.03.20161.81 Mб4metod_kki.pdf
#
15.03.20161.6 Mб7metod_noi.pdf
#
09.04.2015432.33 Кб18Metod_rek_k_prakt_bakal.docx
#
23.08.201965.02 Кб2Metod_ukaz_kontr_rab_5416_s_sayta_1.doc
#
10.11.20195.05 Mб2Metod_ukaz_po_dom_rab_EP_(red).doc