12. Главные и эквивалентные напряжения

12. Главные и эквивалентные напряжения

Напомним некоторые основные положения теории напряжений, излагаемые обычно в курсе теории упругости или в подробных учебниках сопротивления материалов.

Если выделять из тела в окрестности некой точки (рис. 12.1) элементарный объем в виде бесконечно малого парал­лелепипеда, то действие на него окружающей среды заменя­ется напряжениями, компоненты которых действуют на грани параллелепипеда.

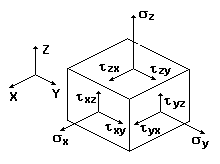
Рис. 12.1

В силу закона парности касательных напряжений

; ; . (12.1)

В общем случае в точке имеется только шесть независимых компонент напряжений, которые образуют симметричный тензор напряжений

(12.2)

На проходящей через ту же точку произвольно ориентированной площадке, нормаль которой  имеет направляющие косинусы l, m, n с осями x, y, z, действует нормальное напряжение _ и касательное напряжение _ (рис. 12.2) с равнодействующей S_. Проекции этой равнодействую­щей на координатные оси S_x, S_y, S_z связаны с компонентами напряжений условиями равновесия (формула Коши):

(12.3) Рис. 12.2.

Существуют три таких взаимно перпендикулярных площадки, на которых касательные напряжения отсутствуют. На этих, так называемых, главных площадках действуют главные напряжения ₁, ₂ и ₃. При этом имеется в виду, что ₁₂₃. Известно также, что главные напряжения обладают экстремальными свойствами, а именно – на любой площадке результирующее напряжение и .

Направляющие косинусы l_k , m_k и n_k нормалей главных площадок _к определяются из решения системы уравнений:

(_х – _k) l_k + _xy m_k + _xz n_k = 0;

_xy l_k + (_y – _k) m_k + _yz n_k = 0;

_xz l_k + _yz m_k + (_z – _k) n_k = 0;

l_k² + m_k² + n_k² = 1. (12.4)

Из (4) следует, что главные напряжения _k (к=1,2,3) являются корнями кубического уравнения:

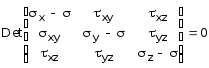. (12.5)

Уравнение (5) в развернутой форме имеет вид

, (12.6)

а его коэффициенты являются инвариантами (т.е. не зависят от выбора системы координат). Первый инвариант равен утроенному среднему напряжению (гидростатическому давлению) .

Направление главных площадок может быть определено не девятью направляющими косинусами, а тремя Эйлеровыми углами:

 – угол (нутации) между положительными направ­лениями оси Z и ₃ (0);

 – угол (прецессии) между осью X и осью А, идущей вдоль линии пересечения плоскостей XOY и ₁О₂ так, чтобы ОА, Z и ₃ образовали правую тройку, при этом угол  увеличивается от оси X к оси Y (02);

 – угол (чистого вращения) между осями ₁ и А, который увеличивается от ₁ к ₂ (02).

Для характеристики НДС используется коэффициент Лоде-Надаи

,

принимающий значения ₀=1 при чистом сжатии, ₀=0 при чистом сдвиге, ₀=1 при чистом растяжении.

В принятых обозначениях при выводе результатов расчета тензор напряжений (2) в общем случае выглядит как

(12.7)

В SCAD главные напряжения обозначаются как .

Для углов Эйлера введены обозначения:

 – ТЕТА,

 – PSI,

 – FI.

12.1 Главные напряжения для конечных элементов различных типов

Каждый тип элемента обладает определенными особенностями напряженно-деформиро­ванного состояния (НДС), которое также определяет и особен­ности расположения главных площадок.

В зависимости от рассматриваемого типа элемента в каждой точке, где определены усилия (напряжения), вычисляются главные напряжения и углы, характеризующие положение главных площадок.

Если результаты выданы в одной точке – то это центр тяжести элемента (центр тяжести поперечного сечения тела вращения для осесимметричных элементов). Для большего числа точек вычисления будут проведены в узлах элемента и центре тяжести.

Пространственная задача теории упругости

Для решения пространственной задачи теории упругости предназначены объемные элементы и, как частный случай, осесимметричные элементы. Для них с использо­ванием формул из раздела 12.1 вычисляются:

• главные напряжения N₁ , N₂ и N₃.;

• углы Эйлера – ТЕТА (), PSI() и FI();

• коэффициент Лоде-Надаи ₀.

• угол наклона главного напряжения N1 к оси X1.

Элементы балки стенки

Для случая плоского НДС (балка-стенка) тензор напряжений имеет вид:

(12.8)

Так как элемент всегда расположен в плоскости XOZ, то для срединной поверхности его вычисляются только два главных напряжения по формуле

. (12.9)

Положение главных площадок характеризуется углом наклона главного напряжения N1 к оси X1

. (12.10)

Если T_xz=0, то считается, что =0, и в этом случае направления главных площадок совпадают с осями местной системы координат элемента.

Плиты и оболочки

Для плит на срединной поверхности вычисляются следующие усилия:

• моменты – M_x , M_y и M_xy;

• перерезывающие силы – .Q_x и Q_y.

Для оболочек вычисляются также напряжения – N_x , N_y и N_xy. Тензор напряжений имеет вид

, (11)

так как касательные напряжения не учитываются.

Для каждой точки, в которой вычислены усилия, главные напряжения определяются на нижней (Н), срединной (С) и верхней (В) поверхностях. При этом

N_x^B/H = N_x  6M_x/h²,

N_y^B/H = N_y  6M_y/h², (12)

N_xy^B/H = N_xy  6M_xy/h².

Тогда главные площадки для верхней и нижней поверхности параллельны одна другой, а главные напряжения определяются по формуле:

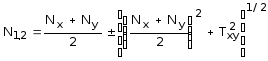, (13)

Положение главных площадок характеризуется углом наклона главного напряжения N1 к оси X1

. (14)

Если T_xy = 0, то считается, что  = 0, и в этом случае направления главных площадок совпадают с осями местной системы координат элемента.

Стержневые элементы

Главные напряжения в стержневых элементах определяются по формуле

. (12.15)

Здесь _x, _x и _y нормальное и касательные напряжения в характерных точках поперечного сечения стержня.

Для того чтобы определить главные напряжения, сечение элемента должно быть задано:

• как одно из параметрических сечений (положение характерных точек для таких сечений показано на рис. 12.1);

• или с использованием сортамента металлопроката (рис. 12.2) изображены допустимые профили из сортамента и характерные точки сечений, в которых производятся вычисления).

Во всех других случаях главные напряжения не вычисляются.

В точках, которые не располагаются на материальной части поперечного сечения (например точка 9 для коробчатого сечения), значения главных напряжений не вычисляются.

Рис. 12.1. Параметрические сечения (начало)

Рис. 12.1. Параметрические сечения (продолжение)

Рис.12.2 Прокатные профили