КОНСПЕКТ ЛЕКЦИЙ КОДЭИ

Если предположить, что начальное состояние вектора весов W0 совпадает с началом координат, то, поскольку локальный минимум, значение ошибки в котором падает ниже ε, «встретится» алгоритму первым, глобальный минимум не будет обнаружен.

Для поиска глобального минимума используются следующие методы:

1.Метод перебора всех возможных значений целевой функции гарантированно позволит обнаружить глобальный минимум, но в большинстве случаев этот способ неприменим на практике из-за огромного количества состояний весов, которое потребуется рассмотреть.

2.Можно несколько раз последовательно произвести процесс оптимизации, каждый раз изменяя начальное состояние модели в надежде, что какое-то из них окажется в «области притяжения» глобального минимума. Этот способ не гарантирует обнаружения глобального оптимума, но позволяет задать поиску более определенное направление.

Градиентные алгоритмы обучения нейронных сетей

Наибольшую популярность при обучении многослойных персептронов получили градиентные алгоритмы. В их основе лежат метод градиентного (наискорейшего) спуска, метод сопряженных градиентов и пр. Причины распространенности градиентных алгоритмов заключаются в том, что они требуют относительно небольшого числа итераций для обучения сети, обеспечивают достаточно малый уровень ошибки и устойчивы к аномальным значениям входных признаков. Недостатком градиентных методов является то, что они обнаруживают только локальные минимумы целевой функции..

Метод градиентного спуска

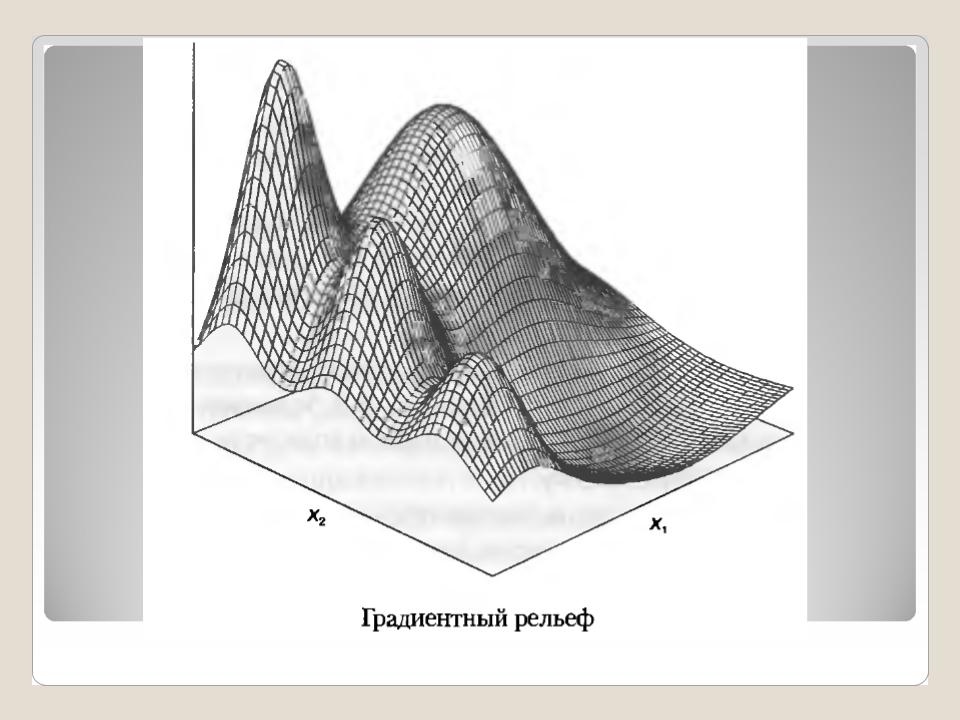
Градиентный спуск — это метод нахождения локального минимума функции с помощью движения вдоль антиградиента. В случае обучения нейронных сетей целевой функцией является функция выходной ошибки сети Е(W). Напомним, что градиент представляет собой сумму производных функции по трем координатам. График целевой функции в трехмерных координатах (х, у, z) напоминает рельеф земной поверхности. Минимумы функции образуют «впадины», а максимумы — «холмы».

Процесс оптимизации начинается со случайного выбора точки на рельефе, которая получается в результате инициализации весов небольшими случайными значениями. Затем в данной точке вычисляется градиент функции, и на его основе определяется точка, соответствующая новому состоянию весов. При этом согласно рассмотренному выше свойству градиента новая точка формируется с определенным шагом в направлении максимального убывания функции. Далее вычисляется следующая точка, и процесс повторяется, пока не будет достигнут ближайший минимум. Можно провести следующую аналогию: если на поверхности установить шарик, он скатится в ближайшую впадину по направлению наибольшей крутизны спуска.

Направление коррекции весов мы определили, но остается открытым вопрос о величине этой коррекции, или, как говорят, о шаге коррекции. Влияет ли величина коррекции весов на результаты обучения, и если да, то как ее выбрать? Влияние шага коррекции на каждой итерации очевидно. Если шаг коррекции окажется слишком большим, то алгоритм может «перешагнуть» через «впадину» на рельефе и не обнаружить соответствующего минимума. Если шаг коррекции будет слишком малым, то для достижения минимума потребуется большое количество итераций, что приведет к очень долгой процедуре обучения.

При практической реализации градиентных алгоритмов обучения величину шага коррекции делают переменной, и в процессе обучения она адаптируется к ситуации. Для этого желательно, чтобы на начальных этапах обучения шаг коррекции весов был наибольшим, а к концу процесса постепенно уменьшался, как показано на рисунке.

На рисунке представлена «впадина» градиентного рельефа. При градиентном спуске осуществляется переход из точки в точку в направлении антиградиента. При этом расстояние между двумя соседними точками хi и xi+1, меняется в зависимости от номера шага. Начальные шаги самые большие, а последующие уменьшаются по мере приближения к минимуму.

Из курса математики известно, что в тех точках, где функция ошибки убывает, еѐ производная имеет отрицательный знак, а в тех, где возрастает, — положительный. При проходе через экстремум производная функция ошибки меняет свой знак: в точке минимума — с отрицательного на положительный (функция сначала убывает, а потом возрастает); в точке максимума, наоборот, с плюса на минус (функция ошибки сначала возрастает, а потом убывает). Экстремум расположен в точке, где производная равна

0.