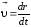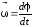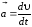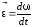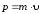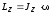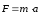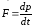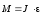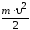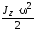§2. Кинетическая энергия вращения

Рассмотрим абсолютно твердое тело, вращающееся около неподвижной оси z, проходящей через него (рис. 2.1). Мысленно разобьем это тело на маленькие объемы с элементарными массами m₁, m₂, …, m_n находящиеся на расстоянии r₁, r₂ …, r_n от оси.

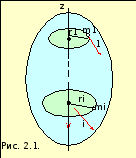
Угловая скорость вращения этих объемов одинакова:

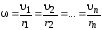(2.1)

Кинетическую энергию вращающегося тела найдем как сумму энергий его элементарных объемов:

Используя выражение (2.1), получаем

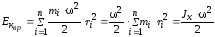
где J_x – момент инерции тела относительно оси z. Таким образом, кинетическая энергия вращающегося тела

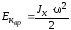
В случае плоского движения тела, например цилиндра, скатывающегося с наклонной плоскости без скольжения, энергия движения складывается из энергии поступательного движения и энергии вращения:

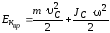
где т – масса катящегося тела;

_c – скорость центра масс тела;

J_c – момент инерции тела относительно оси, проходящей через его центр масс;

 – угловая скорость

§3. Момент силы. Уравнение динамики вращательного движения твердого тепа

Моментом силы F относительно точки O называется физическая величина, определяемая векторным произведением радиуса-вектора r, проведенного из точки O в точку A приложения силы, на силу F (рис. 3.1):

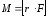
Здесь М — псевдовектор, его направление совпадает с направлением поступательного движения правого винта при его вращении от r к F.

Модуль момента силы

(3.1)

где  – угол между r и F;

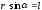– кратчайшее расстояние между линией действия силы и точкой O – плечо силы.

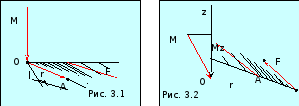
Моментом силы F относительно оси z называется скалярная величина M_z, равная проекции на эту ось вектора М момента силы, определенного относительно произвольной точки O данной оси x (рис. 2.2). Значение момента М, не зависят от выбора положения точке O на ось z.

Если ось z совпадает с направлением вектора М, то момент силы:

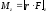
Выражение для работы при вращении тела (рис. 3.3):

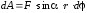(3.2)

Учитывая (3.1), можем записать

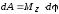
где 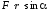— момент силы относительно осиz.

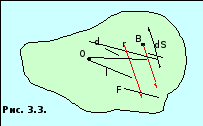
Таким образом, работа при вращении тела равна произведению момента действующей силы на угол поворота.

Работа при вращении тела вдет на увеличение его кинетической энергии:

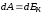
но 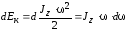, поэтому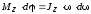, или .

Учитывая, что 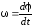, получаем:

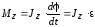(3.3)

Уравнение (3.3) представляет собой уравнение динамики вращательного твердого тела относительно неподвижной оси.

Или в векторном виде:

(3.4)

где J – главный момент инерции тела (момент инерции относительно главной оси).

§4. Момент импульса и закон его сохранения

Моментом импульса (количеством движения) материальной точки A относительно неподвижной точки O называется физическая величина, определяемая векторным произведением:

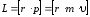
где r – радиус-вектор, проведённый из точки O в точку A;

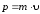–импульс материальной точки (рис. 4.1.);

L – псевдовектор, его направление совпадает с направлением поступательного движения правого винта при его вращении от r к p.

Модуль вектора момента импульса:

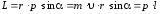
где  – угол между векторами r и p,

l – плечо вектора p относительно точки O.

Моментом импульса материальной точки A относительно неподвижной оси Z называется скалярная величина L_z, равная проекции на эту ось вектора момента импульса. Значение момента импульса L_z не зависит от положения точки O на оси Z.

Моментом импульса материальной точки:

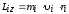
и направлен по оси в сторону, определяемую правилом правого винта.

Момент импульса твердого тела относительно оси есть сумма моментов импульсов отдельных материальных точек:

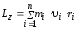
Используя формулу 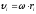, получим:

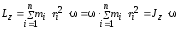
таким образом:

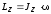
где J_z – момент инерции тела;

 – угловая скорость.

Продифференцировав последнее уравнение по времени, получим:

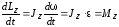
т.е. .

Это выражение - ещё одна форма уравнения (закона) динамики вращательного движения твёрдого тела относительно неподвижной оси.

В замкнутой системе момент внешних сил M=0 и , откуда:

.

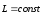Выражение представляет собой закон сохранения момента импульса: момент импульса замкнутой системы сохраняется, т.е. не меняется с течением времени.

Основная связь между величинами и уравнениями, определяющие вращение тела вокруг неподвижной оси и его поступательном движении:

№	Поступательное движение		Вращательное движение
	Масса	m	Момент инерции	J
	Скорость		Угловая скорость
	Ускорение		Угловое ускорение
	Сила	F	Момент силы	Mz или M
	Импульс		Момент импульса
	Основное уравнение динамики		Основное уравнение динамики
	Работа		Работа вращения
	Кинетическая энергия		Кинетическая энергия вращения

- 3-