§ 2. Кинетическая и потенциальная энергии

Кинетическая энергия механической системы — это энергия механического движения этой системы.

Сила F, действуя на покоящееся тело и вызывая его движение, совершает работу, а энергия движущегося тела возрастает на величину затраченной работы. Таким образом, работа dA силы F на пути, который тело прошло за время возрастания скорости от 0 до , идёт на увеличение кинетической энергии dE_к тела, т. е.

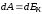
Используя второй закон Ньютона 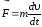и умножая на перемещениеdr, получаем:

.

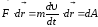Так как 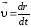, то

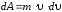
откуда

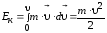
Таким образом, тело массой m, движущееся со скоростью , обладает кинетической энергией

(2.1)

Потенциальная энергия – механическая энергия системы тел, определяемая их взаимным расположением и характером сил взаимодействия между ними.

При перемещении тела из одного положения в другое, работа, совершаемая действующими силами при перемещении тела из одного положения в другое, не зависит от того, по какой траектории это перемещение произошло, а зависит только от начального и конечного положения. Такие поля называются потенциальными, а силы, действующие в них, – консервативными.

Работа консервативных сил на замкнутой траектории равна нулю. Это утверждение поясняет рис. 2.1.

Свойством консервативности обладают сила тяжести и сила упругости. Для этих сил можно ввести понятие потенциальной энергии.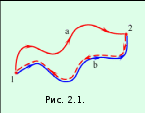

Работа консервативной силы A_12a = A_12b. Работа на замкнутой траектории A = A_12a + A_21b = A_12a – A_12b = 0.

Тело, находясь в потенциальном поле сил, обладает потенциальной энергией E_п. Работа консервативных сил при элементарном (бесконечно малом) изменении конфигурации системы равна приращению потенциальной энергии, взятому со знаком минус, так как работа совершается за счет убыли потенциальной энергии:

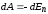(2.2)

Работа dA выражается как скалярное произведение силы F на перемещение dr и выражение (2.2) можно записать в виде

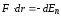(2.3)

Следовательно, если известна функция Е_п ( r ), то из формулы (2.3) можно найти силу F по модулю и направлению.

Потенциальная энергия может быть определена исходя из (2.3) как

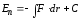(2.4)

где C – постоянная интегрирования.

Если тело перемещается вблизи поверхности Земли, то на него действует постоянная по величине и направлению сила тяжести 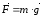. Работа этой силы зависит только от вертикального перемещения тела. На любом участке пути работу силы тяжести можно записать в проекциях вектора перемещения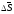на осьOY:

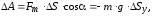
где 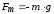– проекция силы тяжести,ΔS_y – проекция вектора перемещения. Если тело переместилось из точки, расположенной на высоте h₁, в точку, расположенную на высоте h₂ от начала координатной оси OY (рис. 2.2.), то сила тяжести совершила работу:

.

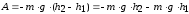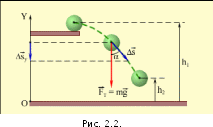
Эта работа равна изменению некоторой физической величины 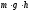, взятому с противоположным знаком. Эту физическую величину называютпотенциальной энергией тела в поле силы тяжести

E_p = mgh.

Она равна работе, которую совершает сила тяжести при опускании тела на нулевой уровень.

Работа силы тяжести равна изменению потенциальной энергии тела, взятому с противоположным знаком.

A = –(E_p2 – E_p1).

Найдём потенциальную энергию упругодеформированного тела (пружины). Сила упругости пропорциональна деформации:

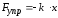
где F_упр — проекция силы упругости на ось х,

k — коэффициент упругости (для пружины – жёсткость),

знак минус указывает, что F_упр направлена в сторону, противоположную деформации х.

По третьему закону Ньютона, деформирующая сила равна по модулю силе упругости и противоположно ей направлена, т. е.

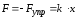
Элементарная работа dA, совершаемая силой F_x при бесконечно малой деформации dx, равна:

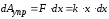
а полная работа

.

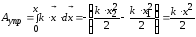идет на увеличение потенциальной энергии пружины. Таким образом, потенциальная энергия упругодеформированного тела:

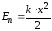
Полная механическая энергия системы:

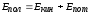
т.е. равна сумме кинетической и потенциальной энергий.