2.3.Операционные усилители

2.3.1. Основные сведения об операционных усилителях

Операционные усилители находят широкое распространение в современной электронике. Они выполняются в виде интегральных микросхем и имеют два входа – инвертирующий и неинвертирующий. С помощью операционных усилителей можно производить различные аналоговые математические операции: сложение и вычитание с весовыми коэффициентами, дифференцирование и интегрирование. Отсюда они и получили название «операционные». ОУ имеют большой коэффициент усиления от нескольких тысяч до сотен тысяч. Они используются в различных электронных устройствах: предварительные усилители в УНЧ, компараторы, активные фильтры, эквалайзеры, источники опорного напряжения и т.д.

ОУ включаются в различные схемы обычно с использованием отрицательной обратной связи (ООС). Существуют два основных способа включения ОУ в схему. В первом случае сигнал подается на инвертирующий вход, а во втором – на неинвертирующий. Определим коэффициент усиления с обратной связью Кос для обоих случаев.

Первый случай, когда сигнал подается на инвертирующий вход, изображен на рис.2.12.

R₂

R₁

¯

Uвх оу



+

Uвх

Uвых

U₁

Рис.2.12. Схема включения операционного усилителя при подаче сигнала на инвертирующий вход

Коэффициент усиления при разомкнутой ООС

, (1)

отсюда

U_вых.= - К_уиU_вх.ос

Входное напряжение ОУ U_вх.ос складывается из двух слагаемых, первое из которых образуется за счет воздействия входного сигнала, а второе – за счет воздействия выходного сигнала через цепь ООС.

(2)

Обозначим и подставим выражение (2) в выражение (1).

Uвых = - Куи Uвхα – Куи Uвых(1-α),

Uвых(1+ Куи(1-α)) = - Uвх Куи α,

откуда

.

Т.о. коэффициент усиления ОУ с отрицательной обратной связью определяется отношением сопротивлений делителя в цепи ООС.

Второй случай, когда сигнал подается на неинвертирующий вход, изображен на рис.2.13.

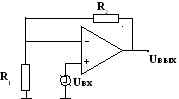
Рис.2.13. Схема включения операционного усилителя при подаче

сигнала на неинвентирующий вход

В этом случае коэффициент усиления с обратной связью имеет вид

Рассмотрим некоторые приложения использования ОУ для выполнения различных математических операций.

Схема сложения сигналов с весовыми коэффициентами изображена на рис.2.14.

Рис.2.14. Схема сложения сигналов

.

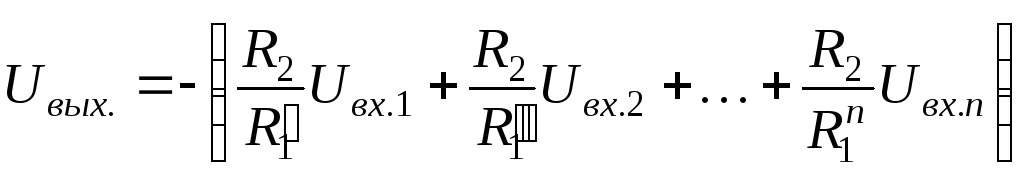Схема операции дифференцирования изображена на рис.2.15.

Рис.2.15. Схема операции дифференцирования

,

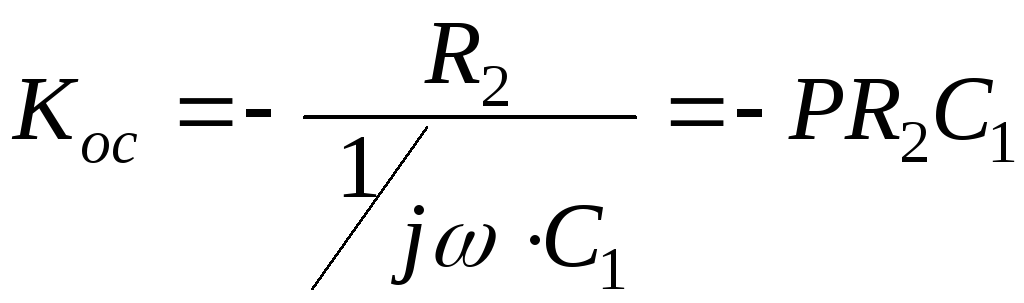где P = jω – оператор Лапласа.

Схема операции интегрирования изображена на рис.2.16.

Рис.2.16. Схема операции интегрирования

.

2.3.2. Математические модели операционных усилителей.

Простейшую математическую модель ОУ, когда нас интересует только коэффициент усиления по одному из входов, можно представить в виде источника тока, управляемого напряжением рис.2.17.

Рис.2.17. Простейшая модель операционного усилителя

Выходное напряжение

Коэффициент усиления при разомкнутой ОС

Крутизна

.

Если нас интересует коэффициент усиления по дифференциальному (разностному) сигналу, по математическую модель ОУ можно представить рис.2.18.

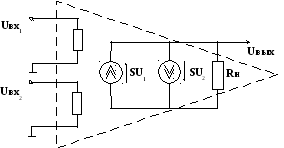
Рис.2.18. Модель операционного усилителя с двумя входами

При этом выходное напряжение

.

Коэффициент усиления при разомкнутой цепи ОС

.

Крутизна

.

Сложность модели ОУ зависит от области применения ОУ.