
- •Министерство образования российской федерации
- •Введение. Базовые элементы математических моделей компонентов радиоэлектронных устройств
- •Введение
- •Базовые элементы математических моделей компонентов радиоэлектронных устройств
- •2.1. Биполярные транзисторы
- •2.1.1. Физические принципы работы биполярного транзистора
- •2.1.3. Справочные данные биполярного транзистора
- •Расчет параметров математической модели биполярного транзистора по справочным данным
- •2.2.1. Физические принципы работы полевого транзистора
- •2.2.2. Справочные данные и расчет параметров математической модели полевого транзистора
- •Физические принципы работы полевого транзистора с изолированным затвором
- •2.3.Операционные усилители
- •2.3.1. Основные сведения об операционных усилителях
- •2.3.2. Математические модели операционных усилителей.
- •Справочные данные операционного усилителя
- •Методы и алгоритмы анализа основных характеристик радиоэлектронных устройств
- •3.1. Принципы построения математической модели
- •3.2.1. Частотный анализ
- •3.2.2. Временной анализ
- •3.2.3. Анализ по постоянному току.
- •3.3 Нелинейные цепи.
- •3.3.1 Решение системы нелинейных уравнений.
- •3.3.2 Временной анализ
- •Инерционные цепи.
- •Основные сведения о системе схемотехнического моделирования Micro – Cap5
- •4.1. Основные возможности программы Micro-Cap 5. Главное меню
- •4.2 Работа в режиме схемного редактора
- •4.3 Анализ переходных процессов (Transient Analysis)
- •4.4 Анализ частотных характеристик (ac Analysis)
- •4.5 Анализ передаточных характеристик по постоянному току (dc Analysis)
- •4.6 Многовариантный анализ
- •4.7 Вывод графиков характеристик в режиме Probe
2.1. Биполярные транзисторы
2.1.1. Физические принципы работы биполярного транзистора
Биполярный транзистор р-n-р типа схематически изображен на рис.2.1.

Рис.2.1. Схематическое изображение биполярного транзистора
Если на эмиттер подать относительно базы положительный потенциал и замкнуть цепь коллектора, то дырки из эмиттера будут инжектироваться в базу.
При достаточно малой толщине базы дырки будут проходить через нее и попадать в коллектор. Если цепь коллектора замкнута, то в ней возникнет электрический ток. Часть дырок при прохождении через базу будет рекомбинировать с электронами, вследствие чего возникнет ток базы. Мощность в цепи коллектора в этом случае выделяться не будет и эффект усиления отсутствует.
Если в цепь коллектора ввести активное сопротивление нагрузки Rн, то ток коллектора создаст на нем падение напряжения, которое плюсом будет приложено к коллектору. При этом, наряду с собиранием будет происходить инжекция дырок из коллектора в базу, вследствие чего суммарный коллекторный ток будет много меньше тока эмиттера и усиления по мощности также не будет. Для нормальной работы транзистора в усиленном режиме необходимо на коллектор относительно базы подать достаточно большой отрицательный потенциал. При этом, если сопротивление нагрузки Rн много больше сопротивления эмиттера (Rн>> rэ), то мощность выделяемая в нагрузке будет много больше мощности отдаваемой в цепь эмиттера.
Так как
Ik ≈ Iэ и RН >> rэ, то
I2k RН >>I2э rэ и PH >> Pэ.
Основные характеристики биполярного транзистора
Биполярные транзисторы определяются следующими основными характеристиками.
Выходные а) и входные б) статические характеристики рис.2.2.
а) б)

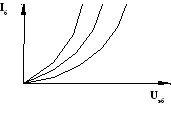
Рис.2.2. Выходные и входные характеристики биполярного
транзистора
Коэффициенты передачи по току α и β.
![]() -
коэффициент передачи по току при
включении с ОБ;
-
коэффициент передачи по току при
включении с ОБ;
![]() -
коэффициент передачи по току при
включении с ОЭ.
-
коэффициент передачи по току при
включении с ОЭ.
![]() ;
;
![]() .
.
Наиболее важной характеристикой биполярного транзистора, определяющей его усилительные свойства, является статический коэффициент усиления по току
![]()
Кроме режима прямого включения транзистора, существует его инверсный режим, когда напряжения на переходах изменяют свой знак на противоположный, при этом Bст инв.<< Bст.
Инверсный режим применяется относительно редко, в основном, в цифровых схемах.
Математическая модель биполярного транзистора.
Математическую модель биполярного транзистора можно построить на основе базовых элементов математической модели рис.2.3. При этом p-n и n-p – переходы моделируются с помощью диодов, включенных в прямом и обратном направлениях, а собираемые токи – с помощью источников тока, управляемых током.
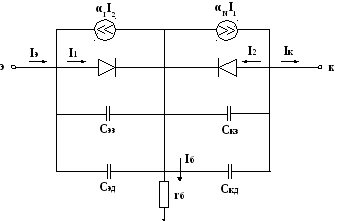
б
Рис.2.3. Математическая модель биполярного транзистора
Если на эмиттер относительно базы подать достаточно большой положительный потенциал и замкнуть цепь коллектора, то из эмиттера в базу будет инжектироваться ток I1. При этом часть дырок в базе рекомбинирует с электронами, вызывая ток базы, а в коллектор попадает ток αNI1, где αN – коэффициент передачи тока при прямом (нормальном) включении транзистора (αN <1). При инверсном включении транзистора и замкнутой цепи эмиттера из коллектора в базу инжектируется ток I2, а в эмиттер поступает ток αN I2, где αN – коэффициент передачи тока при инверсном включении транзистора (αN << αN). Токи I1, I2 называются инжектируемыми токами, а токи αN I1 и αN I2 собираемыми.
При этом
Iэ = I1 – αI I2 (2.1)
Ik = αN I1 – I2 (2.2)
Ток I1 при замкнутой цепи коллектора и ток I2 при замкнутой цепи эмиттера можно представить как токи, протекающие через диоды
![]() ;
(2.3)
;
(2.3)
![]() ,
(2.4)
,
(2.4)
где I'эо - тепловой ток эмиттера при замкнутой цепи коллектора; I'ко- тепловой ток коллектора при замкнутой цепи эмиттера.
В справочной же литературе приводится тепловой ток эмиттера при разомкнутой цепи коллектора Iэо и тепловой ток коллектора при разомкнутой цепи эмиттера Iко, поэтому токи I'ко и I'ко необходимо выразить через токи Iэо Iко.
При разомкнутой цепи эмиттера из уравнения (2.1) получаем
I1 = αI I2
При достаточно большом отрицательном напряжении на коллекторе Uкб<0 и Uкб >> φT из уравнения (2.4) имеем I2 = -I'ко.
При разомкнутой цепи эмиттера и Uкб < 0, Uкб >>φт через коллектор протекает тепловой ток коллектора Iко. Воспользовавшись уравнением (2.2), получаем
![]() (2.5)
(2.5)
Аналогично
![]() (2.6)
(2.6)
Подставляя в уравнение (2.1), (2.2) токи (2.3), (2.4) и воспользовавшись соотношениями (2.5), (2.6), получаем уравнения, описывающие математическую модель биполярного транзистора
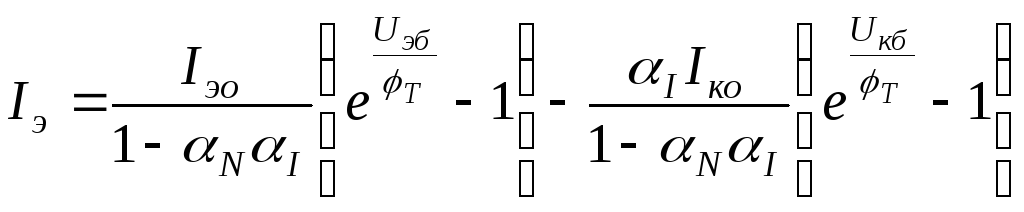 ,
(2.7)
,
(2.7)
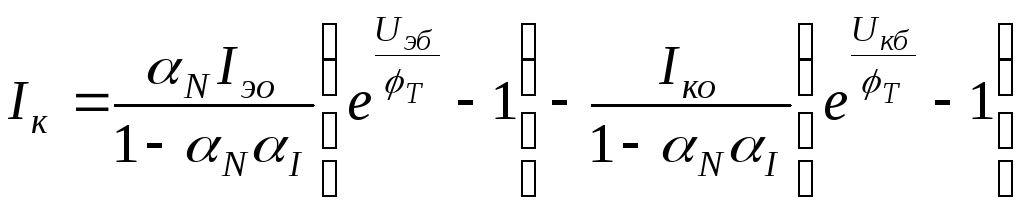 ,
(2.8)
,
(2.8)
![]() (2.9)
(2.9)
Эти уравнения получили название уравнений Эберса-Молла, а математическая модель, описываемая этими уравнениями – моделью Эберса-Молла. Уравнения Эберса-Молла описывают связь токов через переходы с напряжениями на этих переходах.
При Uкб < 0 и Uкб >> φT из второго уравнения Эберса-Молла (2.8) получаем
Iк = α NIэ + Iко
откуда следует, что ток коллектора Iк не зависит от напряжения между коллектором и базой Uкб. В реальных же транзисторах ток коллектора возрастает с увеличением напряжения между коллектором и базой.
Оказывается уравнения Эберса-Молла не учитывают эффект модуляции толщины базы, получившей название эффекта Эрли. Эффект модуляции толщины базы заключается в изменении эффективной толщины базы при изменении напряжения Uкб . При увеличении отрицательного напряжения на коллекторе относительно базы в n-р – переходе расширяется слой обедненный основными носителями заряда (электронами). Т.к. он находится практически целиком в базе, то уменьшается эквивалентная толщина базы. При этом дырки быстрее проходят через базу и попадают в коллектор меньше рекомбинируя с электронами, вследствие чего, коллекторный ток увеличивается. Эффект Эрли учитывается в математической модели биполярного транзистора с помощью дополнительно введенного параметра - напряжения Эрли. Напряжение Эрли VA можно пояснить с помощью рис.2.4.

Рис.2.4. Определение напряжения Эрли
Из рис.2.4 следует, что
VA +Uкб1 = Iк1ctgα
![]() ,
,
где h22 – выходная проводимость при заданном токе коллектора Iк1, откуда
![]()
Значения h22 (Iк1) даются в справочных данных, а Uкб1 в рабочем режиме составляет Uкб1 = (3÷5)В.
Напряжение Эрли характеризует степень наклона выходных статических характеристик относительно оси абсцисс.
Уравнение Эберса-Молла с учетом напряжения Эрли описывают нелинейную модель биполярного транзистора, применяющуюся для анализа по постоянному току и временного анализа. Для анализа частотных характеристик применяется линейная малосигнальная модель рис.2.5.
Rкб′
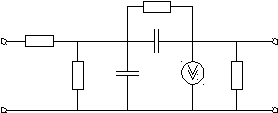
Скб′ Rбб′ б′
б к
Rкэ Uкэ
Uэб′
SUэб′ Cэб′
э э
Рис.2.5. Малосигнальная модель биполярного транзистора
