Алгоритм выполнения работы

1. Записывается передаточная функция разомкнутой системы.

2. Определяются корни характеристического уравнения.

3. По найденным корням делается вывод об устойчивости разомкнутой системы.

4. Записывается передаточная функция замкнутой системы и строится переходной процесс.

5. Делается вывод об устойчивости замкнутой системы по рассчитанным коэффициентам.

6. Анализируется поведение системы при изменении коэффициентов K_п, K_и и K_д. Рассчитываются значения интегральной и интегрально-квадратичной ошибок.

Пример расчета

Для звена, заданного передаточной функцией и пропорционально-интегрально-диффе-ренциального регулятора с передаточной функцией , провести исследование влияния коэффициентов регулятора на устойчивость системы, представленной на рис. 5.1, скорость сходимости переходного процесса, его колебательность, а также на значения интегральной и интегрально-квадратичной ошибок.

Решение

1. Передаточная функция разомкнутой системы:

.

2. Характеристическое уравнение разомкнутой системы:

имеет два действительных отрицательных корня

,

и один нулевой корень p₃ = 0.

Вывод: разомкнутая система находится на границе устойчивости.

3. Передаточная функция замкнутой системы:

.

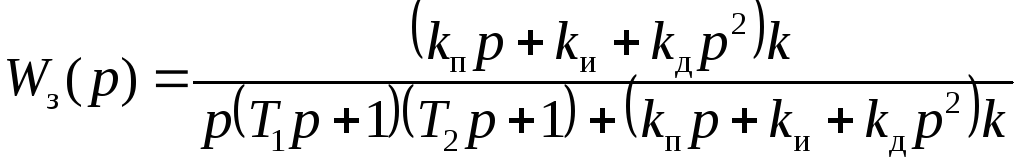4. Переходной процесс при единичном ступенчатом воздействии в изображении по Лапласу:

.

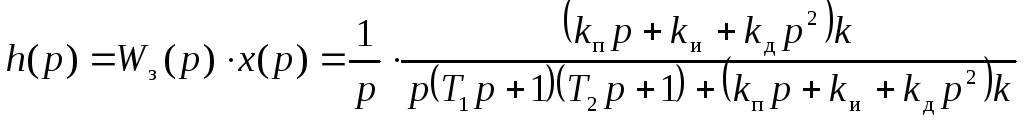5. Получили достаточно сложное выражение. Для обратного преобразования Лапласа воспользуемся функцией invlaplace среды MathCAD. Получим переходной процесс для единичного ступенчатого воздействия при T₁ = 12, T₂ = 25, k = 3, k_п = 5, k_и = 0,5, k_д = 5:

6. Строим переходной процесс по полученному уравнению

(рис. 5.3).

Рис. 5.3. Переходной процесс для замкнутой системы

Вывод: анализ переходного процесса показал, что при данных коэффициентах замкнутая система будет устойчивой.

7. Определим при помощи среды MathCAD значения интегральной и интегрально-квадратичной ошибок, исходя из того, что время регулирования составит 150 с (см. рис. 5.3):

,

.

8. Рассмотрим поведение системы при изменении коэффициентов k_п, k_и, k_д. Переходной процесс при T₁ = 12, T₂ = 25, k = 3, k_п = 5, k_и = 0,5, k_д = 12:

Переходной процесс представлен на рис. 5.3.

9. Определим при помощи среды MathCAD значения интегральной и интегрально-квадратичной ошибок, исходя из того, что время регулирования составит 100 с (см. рис. 5.3):

,

.

10. Переходной процесс при T₁= 12, T₂= 25, k = 3, k_п = 5, k_и = 0,5, k_д = 0,2:

Переходной процесс представлен на рис. 5.4.

11. Определим при помощи среды MathCAD значения интегральной и интегрально-квадратичной ошибок, исходя из того, что время регулирования составит 320 с (см. рис. 5.4):

,

.

12. Переходной процесс при T₁ = 12, T₂ = 25, k = 3, k_п = 5, k_и = 0,8, k_д = 5:

Переходной процесс представлен на рис. 5.4.

Рис. 5.4. Переходной процесс для замкнутой системы

13. Определим при помощи среды MathCAD значения интегральной и интегрально-квадратичной ошибок, исходя из того, что время регулирования составит 550 с (см. рис. 5.4):

,

.

14. Переходной процесс при T₁=12, T₂=25, k=3, k_п=5, k_и=0,1, k_д=5:

Переходной процесс представлен на рис. 5.3.

15. Определим при помощи среды MathCAD значения интегральной и интегрально-квадратичной ошибок, исходя из того, что время регулирования составит 80 с (см. рис. 5.3):

,

.

16. Переходной процесс при T₁=12, T₂=25, k=3, k_п=3, k_и=0,5, k_д=5:

Переходной процесс представлен на рис. 5.4.

17. Определим при помощи среды MathCAD значения интегральной и интегрально-квадратичной ошибок, исходя из того, что время регулирования составит 650 с (см. рис. 5.4):

,

.

18. Переходной процесс при T₁=12, T₂=25, k=3, k_п=8, k_и=0,5, k_д=5:

.

Переходной процесс представлен на рис. 5.4.

19. Определим при помощи среды MathCAD значения интегральной и интегрально-квадратичной ошибок, исходя из того, что время регулирования составит 80 с (см. рис. 5.3):

,

.

20. Переходной процесс при T₁=12, T₂=25, k=3, k_п=5, k_и=0,5, k_д=0:

Переходной процесс представлен на рис. 5.4.

21. Определим при помощи среды MathCAD значения интегральной и интегрально-квадратичной ошибок, исходя из того, что время регулирования составит 400 с (см. рис. 5.4):

,

.

22. Переходной процесс при T₁=12, T₂=25, k=3, k_п=5, k_и=0, k_д=5:

.

Переходной процесс представлен на рис. 5.3.

23. Определим при помощи среды MathCAD значения интегральной и интегрально-квадратичной ошибок, исходя из того, что время регулирования составит 80 с (см. рис. 5.3):

,

.

24. Переходной процесс при T₁=12, T₂=25, k=3, k_п=0, k_и=0,5, k_д=5:

Переходной процесс представлен на рис. 5.5.

Рис. 5.5. Переходной процесс для замкнутой системы при T₁ = 12, T₂ = 25, k = 3, k_п = 0, k_и = 0,5, k_д = 5

25. Определим при помощи среды MathCAD значения интегральной и интегрально-квадратичной ошибок:

,

.

26. На основе проделанного анализа данной замкнутой системы можно сделать вывод:

- при увеличении коэффициента дифференцирования k_д, коэффициента пропорциональности k_п и при уменьшении коэффициента интегрирования k_и колебательность переходного процесса уменьшается и система становится более устойчивой;

- при уменьшении k_д, k_п и увеличении k_и колебательность переходного процесса увеличивается и система теряет устойчивость;

- при увеличении устойчивости повышением k_д значение интегральной ошибки уменьшается по сравнению с исходным переходным процессом, а понижением k_и и повышением k_п ошибка увеличивается, причем при изменении k_и ошибка много больше, чем при изменении k_п. При уменьшении устойчивости уменьшением k_д ошибка возрастает, а увеличением k_и и уменьшением k_п – уменьшается. Интегральная квадратичная ошибка уменьшается при увеличении устойчивости и увеличивается при ее потере (по сравнению с системой при исходном переходном процессе);

- при отсутствии дифференциальной составляющей (k_д = 0) колебательность переходного процесса увеличивается, т.е. время сходимости увеличивается и система теряет устойчивость. При отсутствии интегральной составляющей (k_и = 0) – наоборот. При отсутствии пропорциональной составляющей (k_п = 0) система полностью теряет устойчивость.