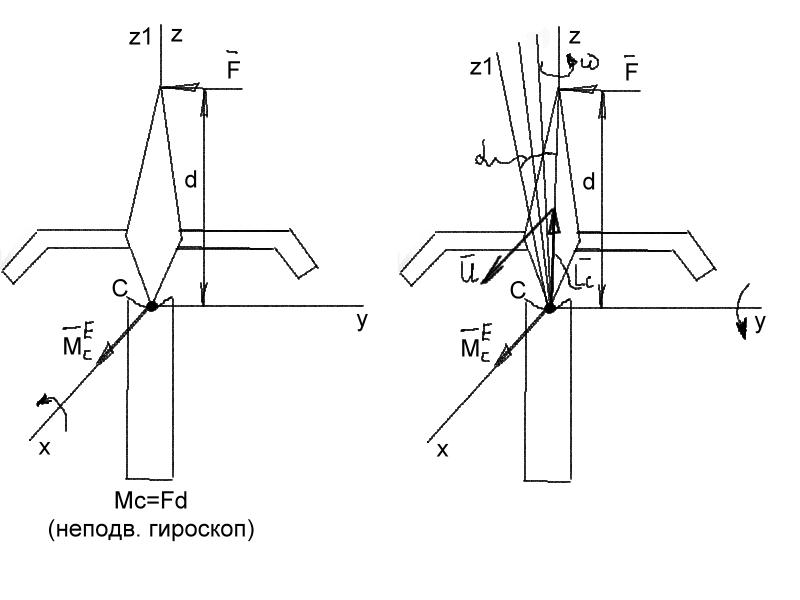
4. Понятие о гироскопе. Гироскоп с тремя степенями свободы.

(1-й случай: центр тяжести совпадает с точкой опоры)

Гироскопом с тремя степенями свободы называется гироскоп, движение которого ограничено наличием только одной неподвижной точки.

Неподвижный гироскоп вращается равноускоренно под действием момента и в течение промежутка времени  угловая скорость вращения гироскопа вокруг оси Сх возрастает от 0 до ₁. После прекращения действия силы F гироскоп продолжает вращаться по инерции вокруг оси Сх с постоянной угловой скоростью ₁.

Рисунок 82

Вращающийся гироскоп (вокруг оси Cz₁). Его кинетический момент направлен вдоль оси симметрии гироскопа Сz₁ и равен

Где - угловая скорость собственного вращения гироскопа.

По теореме Резаля скорость конца вектора кинетического момента гироскопа относительно неподвижной очки С геометрически равна главному моменту внешних сил, приложенных к гироскопу относительно той же точки

, где

, то есть сила F//Cy вызывает перемещение оси Cz₁ вдоль оси Сx, то есть вокруг оси Сy, а не вокруг оси Сx, как в случае с неподвижным гироскопом.

Выводы:

1. Смещение оси быстро вращающегося гироскопа происходит не по направлению силы, а по направлению её момента, т.е. перпендикулярно к направлению силы.

2. Быстрое вращение сообщает гироскопу способность противодействовать силам, стремящимся изменить направление его вращения.

Случай регулярной процессии.

(2-й случай: центр тяжести не совпадает с точкой опоры)

на волчок действуют внешние силы G, реакция опоры в т.О.

(d=OC)

zOz₁, и направлен на линии узлов ОК.

ось симметрии волчка Оz₁ вращается вокруг неподвижной оси Оz с некоторой угловой скоростью (– скорость прецессии, – угол прецессии).

Рисунок 83

Определим угловую скорость прецессии . По теореме Резаля

С другой стороны

, где

таким образом,

Вывод: угловая скорость прецессии ω тем меньше, чем больше ω₁ – угловая скорость вращения волчка вокруг его оси симметрии.